A Knight's Journey
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 30579 | Accepted: 10476 |
Description
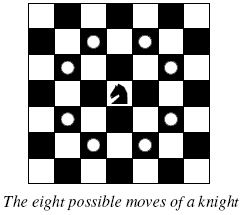 Background
BackgroundThe knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
Input
The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a
p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the
chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
If no such path exist, you should output impossible on a single line.
Sample Input
3 1 1 2 3 4 3
Sample Output
Scenario #1: A1 Scenario #2: impossible Scenario #3: A1B3C1A2B4C2A3B1C3A4B2C4
#include<cstdio> #include<cmath> #include<cstring> #include<iostream> #include<queue> using namespace std; int m1,n1; int a[8][2]={{-2,-1},{-2,1},{-1,-2},{-1,2},{1,-2},{1,2},{2,-1},{2,1}}; int cc[600],cc1[600],flag,vis[30][30]; int dfs(int n,int m,int num) { cc[num] = n; cc1[num] = m; if(num == n1*m1) { flag =1; return 0; } for(int i=0;i<8;i++) { int nn = n+a[i][0]; int mm = m+a[i][1]; if(nn>=1&&nn<=n1 && mm>=1&&mm<=m1 && !vis[nn][mm]&&!flag) { vis[nn][mm] = 1; dfs(nn,mm,num+1); vis[nn][mm] = 0; } } } int main() { int t,i; scanf("%d",&t); for(int k=1;k<=t;k++) { scanf("%d %d",&m1,&n1); memset(vis,0,sizeof(vis)); flag = 0 ; vis[1][1]= 1; dfs(1,1,1); printf("Scenario #%d:\n",k); if(flag) { for(i=1;i<=n1*m1;i++) printf("%c%d",cc[i]+'A'-1,cc1[i]); } else printf("impossible"); if(k!=t) printf("\n\n"); else printf("\n"); } return 0; }
























 867
867

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








