数学模型复习资料
第一章:建立数学模型
学习建模的意义:
- 对于解决现实问题,根据问题内在特点,做出必要假设,合理利用数学方法和工具,得到一个恰当的数学表述。
- 在一般工程技术领域,数学建模仍然大有用武之地
- 计算机技术的出现和迅速发展,为数学建模的应用提供了强有力的工具。
建立数学模型的基本方法和步骤:
模型准备:
在建模之前,我们要确定建立的是哪一类模型,了解实际问题
模型假设:
对模型进行合理化假设
建立模型:
根据假设,合理利用数学规律和工具建立模型
模型求解:
采用数学方法求解该模型
模型分析:
对求解后的模型进行数学上的分析,如误差分析,灵敏度分析等等
模型检验:
将求解结果带回实际问题,检验正确性
模型应用:
将模型应用到实际问题中
关于路障,你还能想到有哪些问题可以用数学模型分析和解决吗?
路障间距设计的数学模型是什么?请见到写出推导过程
背景:
校园、居民小区道路需要限制车速——设置路障
问题:
限制车速≤40km/h, 相距多远设置一个路障?
分析:
汽车通过路障时速度接近于零,通过后开始加速,车速达到40km/h时让司机看到下一路障而减速,至路障处车速接近于零。如此循环,来达到设计路障的目的
假设:
当汽车通过路障时车速为零,其后做等加速运动,当车速达到限速时立即作等减速运动,到达下一个路障时车速为零
建模:

计算:

课后作业:
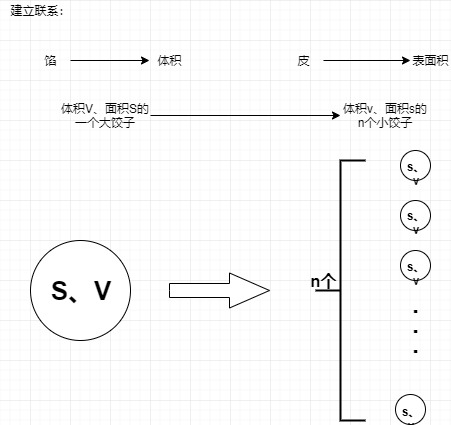
在面团一定的情况下,如果n个饺子包m kg馅,那么n个饺子包多少馅?
数学模型:
通常,1kg馅,1kg面,包100个饺子。今天,馅大于1kg,面还是1kg不变,要把馅包完,应该多包几个(每个小点)?还是少包几个(每个大点)?


解:
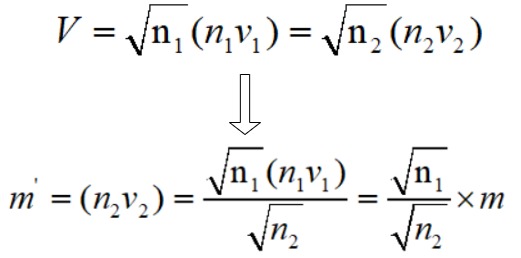
第二章:初等模型
刻画双层玻璃窗功效的数学模型是什么?
- 若该模型中的h过大将会导致什么结果?
- 写出MATLAB中的两个帮助命令,并说明二者区别
列出估计出租车总数额的五个数学模型公式:
用A表示一个从17到1的全体奇数构成的数组:
- 直接法:
- 起点:步长:终点
- Linspace语句:
列举出运动员体重和举重成绩的三个数学模型公式:
在幂函数模型下的折合成绩公式是什么?请说明每个变量的含义:
作业:试写出在幂函数模型下推导折合成绩的过程?
考点:
第一章:
- 重点:包饺子模型,会根据数量变化来求
第二章:
- 双层玻璃功效:要会建立模型,模型假设,模型建立过程,用到了热交换定律
- 估计出租车总数,五个公式的特点和区别记住,会应用。

- 评选举重总冠军,线性模型,幂函数模型和改进的幂函数模型是重点,
- 解读CPI的公式,同比环比的计算。
第三章:
- 存储模型:允许缺货,不允许缺货,公式记住,会计算。其中不允许缺货要背过,
- 森林救火模型:最后的结果要知道参数的含义和影响关系。(一般是选择)
- 不买贵的只买对的,边际效用递减法则(必考),效用最大化满足的条件,进行讨论。买橘子,期末复习的安排都是离散的(必有计算题)
第四章:
- 线性规划模型,Lingo灵敏性分析必考
- 整数模型
- 0-1数学规划
- 可能会出建模题,从上面三个模型里面挑,
第五章:
- 人口增长模型,常用的人口预测公式,人口指数增长模型,改进的指数增长模型,logistic模型,
- 传染病模型,SI模型,SIS模型,SIR模型这三个要会建模,
第六章:
- 减肥计划,要会建模。
























 1984
1984

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








