一种基于GF(2)上本原多项式的随机密钥生成方案
摘要
提出了一种基于GF(2)上本原多项式的新型密钥生成算法。该方法利用MD5算法对系统时间与系统的IP地址进行摘要处理,将这些摘要值的组合用作密钥生成过程的随机种子。通过布拉姆·布拉姆·舒布(BBS)、米卡利‐施诺尔和梅森旋转算法(MT19937)伪随机数生成器算法对生成的密钥进行了随机性测试。生成的密钥在2位、3位、4位和8位的0和1计数值组合基础上进行了比较。本文采用卡方检验、R方检验和标准差来检测生成密钥的随机性。基于上述三项指标对结果进行了分析,发现提出的算法在72.5%的测试用例中实现了更低的离散度,在61.6%的测试用例中实现了更低的错误率,在68.3%的测试用例中实现了更高的适应度值。
关键词: 本原多项式 · Key生成 · BBS · GF(2) · MT19937 · MD5 · IP
1 引言
在密码学中,密钥生成是执行消息加密和解密的初始步骤。生成的密钥可用于对称密钥算法(如DES或AES),其中加密和解密过程仅使用一个密钥;也可用于非对称密钥算法(如RSA),其中需要一对密钥来保护消息的隐私。在非对称密钥算法中,如果发送方想要发送秘密消息,他必须先使用自己的私钥进行加密,再使用接收方的公钥进行加密,以确保消息的机密性。接收方收到加密消息后,将使用自己的私钥和发送方的公钥进行解密。尽管对称密钥算法非常安全,但也存在一个主要缺点:若对称密钥在发送方和接收方之间共享,一旦密钥被他人获取,就可能危及安全性。
本文中,密钥生成过程使用伽罗瓦域GF(2)上的本原多项式来实现。由于系统IP和系统时间始终是唯一的,我们将其视为随机种子。我们使用MD5算法对这两个值的组合进行摘要。MD5是一种密码消息摘要哈希函数,可接受任意长度输入,并生成128位的哈希值作为输出。
本原多项式是不可约多项式。不可约多项式是指在相同域上不能分解为两个非常数多项式的乘积的多项式。 x² + x + 1在GF(2)上被认为是不可约的,但 x² + 1不是,因为(x+ 1)(x+ 1) = x² + 2x+ 1 ≡ x² + 1(mod 2)。设 q为任意素数幂, n为任一正整数。则GF(q)上次数为 n的本原多项式的数量可由以下公式确定:
$$
a_q(n) = \frac{\varphi(q^n - 1)}{n}
$$
其中 $\varphi(n)$ 是欧拉函数。GF(p)称为阶为p的素域,其中 p个元素是从0到 p −1的值。此外,GF(p)中的 a= b等价于 a ≡ b(mod p)。
本文其余部分组织如下:第2节对现有任务进行了评估。第3节介绍了所提出的方法。实验和结果在第4节中给出。第5节总结了本工作并提出了未来的研究方向。
2 文献综述
在[1]中使用的密钥采用在特定范围内指定的随机奇整数,从而提高了基于整数的全同态加密的安全性。关于本原多项式的生成及其结果的性能分析在[2]中进行了描述。[3]中描述了一种基于混沌的伪随机数生成器,该生成器使用基于时间的重播种方法进行种子生成。它分析了二进制序列的随机特性,并考虑了多种用于生成本原多项式的算法。使用遗传算法[4]生成了随机序列,且通过将遗传算法(GA)与线性反馈移位寄存器(LFSR)结合,旨在克服LFSR的线性特性,从而构造出具有较强非线性的生成器。在[5]中构建了种子长度为 O(n log n)的伪随机数生成器(PRNG),并利用有限域上低次多项式的傅里叶谱实现。[6]中利用标记树、逻辑公式和XML文件来生成种子。在[7]中,以系统日期和时间为种子,生成了用于验证码的高安全性随机文本序列。[8]中讨论了硬件伪随机数的生成方法,所生成的序列通过了DIEHARD测试。[9]中解释了带进位反馈移位寄存器(FCSR)的伪随机序列生成分析及其结构,其结构类似于LFSR的伽罗瓦结构。[10]中描述了使用线性反馈移位寄存器(LFSR)的二进制序列生成器及其预测随机性所需的时间分析。本文提出的密钥生成方法中所采用的伪随机数生成器包括布拉姆·布拉姆·舒布(x² mod N生成器)[11], MT19937[12]以及米卡利‐施诺尔[13]。
3 提出的工作
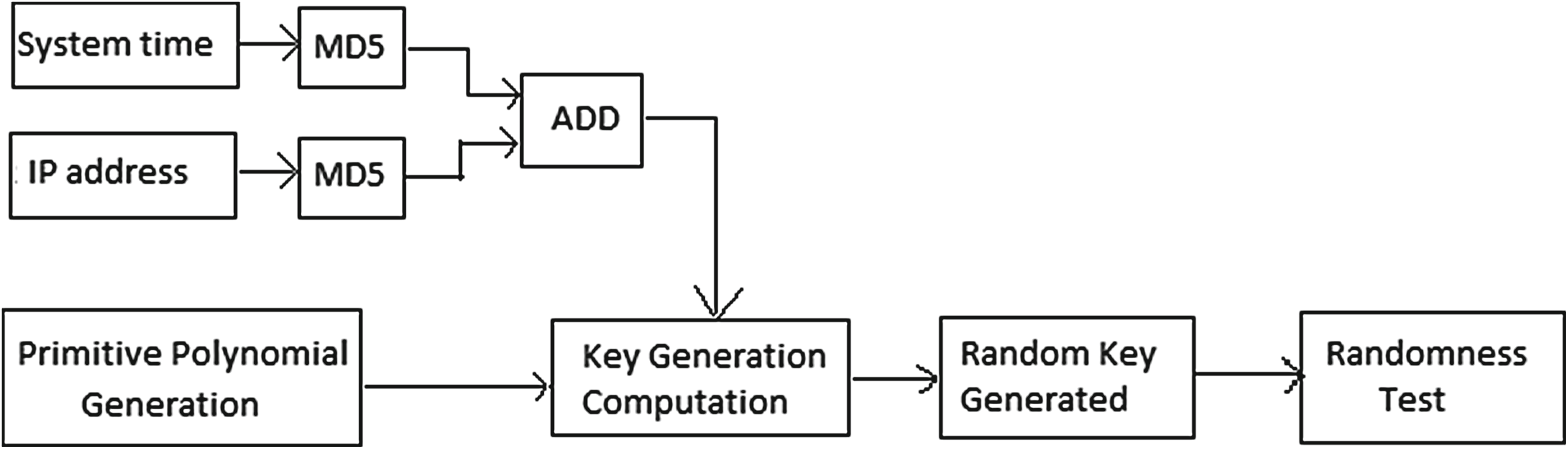
本文中,我们引入一个随机种子作为密钥生成过程的输入。该随机种子由系统时间(毫秒)和系统的IP地址组成,这些值在不同系统中具有唯一性。这两个值使用MD5[14]进行哈希运算,然后相加以便于计算并增强安全性。所提出的方案如图1所示。
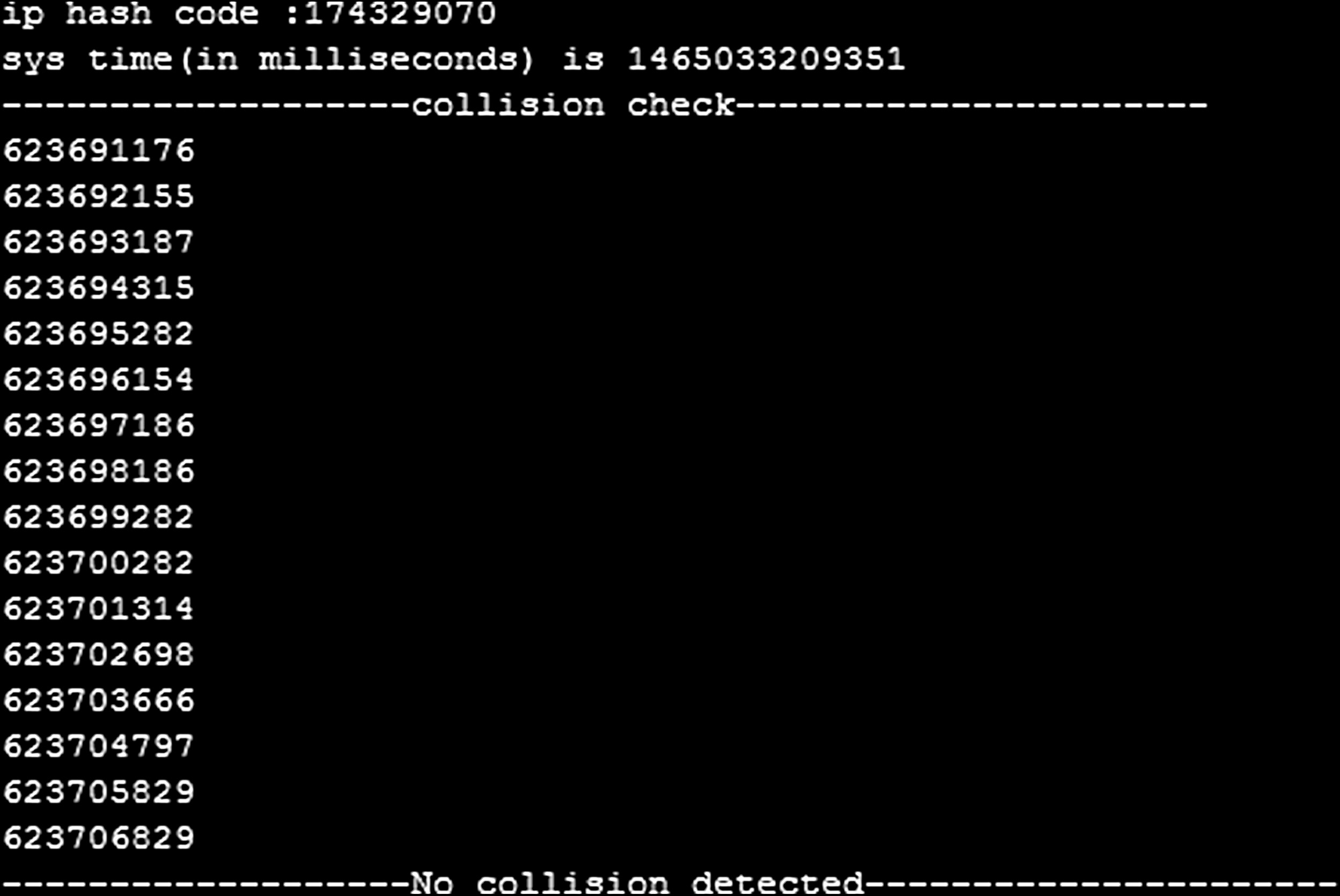
在此方法中,我们并未使用单个大整数作为密钥[1], 而是采用本原多项式进行密钥生成。本原多项式降低了攻击者破解密钥的概率。如图1所示,密钥生成过程的输入包括系统时间和IP地址的128位摘要值。我们使用MD5哈希函数,该函数可接受任意长度输入,并输出128位摘要值。将这两个摘要值相加后,在最坏情况下可得到129位随机种子值。找到该值的概率为 $ \frac{1}{2^{129}} $,几乎可以忽略不计。现在利用公式(1),我们将确定在GF(q)上对于随机选择的次数 n的本原多项式的数量。伽罗瓦域中 q的取值设为2。为了检验通过IP地址和系统时间的哈希值相加所得种子的随机性,我们检查了在特定时间段内运行程序后是否发生碰撞。零碰撞的结果如图2所示。提出的密钥生成算法如下所述:
在密钥生成过程之后,我们将生成的密钥作为输入提供给现有的伪随机数生成器方法。在本文中,我们使用了三种伪随机数生成器来测试我们的结果,分别是布拉姆‐布拉姆‐舒布(BBS)、MT19937和米卡利‐施诺尔。这三种算法均在第4节中进行了说明。类似地,我们通过提供标准输入获得伪随机数生成器方法的输出,然后使用三个准则对两种输出的随机性进行比较。
定理1. 使用我们提出的算法生成的密钥是伪随机的:
证明。 形式上,设 S 和 T 为有限集,F = {f: S → T}为一类函数。若对于每个 f,分布 D 在 S 上关于 F 是 ε‐伪随机的,在F中,分布f(X)(其中X从D中采样)与分布f(Y)(其中Y从S上的均匀分布中采样)之间的统计距离至多为 ε。
我们提出的算法 A包含以下函数:
- $ f_1: {0, 1}^* \rightarrow {0, 1}^k $ 表示MD5哈希函数,该函数将任意长度的比特串进行映射,并给出 k位输出,其中 k=128。
- $ f_2:{0, 1}^k \times {0, 1}^k \rightarrow {0, 1}^{k+1} $ 为映射函数,用于表示将k位哈希值相加以得到 k或 k+1位输出(最坏情况下)。
- 设 $ F_{2q} = \cup_{i=1}^{q} p_i $ 为有限域GF(2)上从1次到 q次的本原多项式集合 $ p_i $。
- $ f_3:F_{2q} \times {0, 1}^k \rightarrow {0, 1}^{k+q} $ 是一个函数,其输入值有两个,分别是 $ p \in F_{2q} $ 和由函数 $ f_1 $ 与 $ f_2 $ 得到的值。
现在,假设 $ A(x_1, x_2) $ 为我们提出的算法,该算法以 $ x_1 $(系统时间)和 $ x_2 $(IP地址)作为种子参数。考虑给定的方程(2)。
$$
P[A(x_1, x_2)= r|x_1 \in Z_n, x_2 \in Z_n] - P[r \in_R {0, 1}^*] \leq \varepsilon \tag{2}
$$
现在,我们必须证明当 $ x_1 $ 和 $ x_2 $ 作为我们提出的算法 A的输入时,攻击者确定生成的密钥值 r的概率是可以忽略的。方程(2)等价于方程(3):
$$
P[f_3(p_i, f_2(f_1(x_1), f_1(x_2)))= r|p_i \in_R F_{2q}, x_1 \in_R Z_n, x_2 \in_R Z_n] - P[r \in_R {0, 1}^{q+k}] \leq \varepsilon \tag{3}
$$
方程(3)表明,当使用函数 $ f_1 $ 对长度为q+ k的密钥值 r进行哈希运算,并使用函数 $ f_2 $ 执行加法运算,再将所得值作为输入通过函数 $ f_3 $ 代入多项式 $ p_i $ 时,确定该密钥值的概率可以忽略不计。由于 $ p_i $ 是从有限多项式域 $ F_{2q} $ 中随机选取的,因此方程(3)可有效简化为方程(4)的正确性。
$$
P[f_1(x)= r|x \in_R Z_n] - P[r \in_R {0, 1}^k] \leq \varepsilon \tag{4}
$$
根据MD5的定义,公式(4)表明,对于任意大的字符串x,其作为函数f1的输入,在 Zn范围内确定 f1(x)= r的概率可以忽略不计。由于 f1是伪随机的(由公式(4)得出),因此我们可以说 f2也是伪随机的,从而导致了 f3的伪随机性(如公式(3)所示)。由于公式(3)等价于公式(2),因此我们可以说提出的算法 A是伪随机的。
从上述函数 $ f_1 $ 我们很容易可以看出,确定 k位哈希值作为输出的概率是可以忽略的。但在我们的情况下, k= 128位,数量相对较少。使用次数为 q的本原多项式可使密钥长度达到 q+ k位,远大于 k位。将密钥长度从 k增加到 q+ k,可以提高生成的密钥的随机性。即 $ \frac{1}{2^{q+k}} \approx 0 $,相比 $ \frac{1}{2^k} \approx 0 $ 是更强的情况。
4 实验与结果
我们通过执行实验并在特定时间内随机生成密钥,以便能够方便地对其进行随机性测试。表1显示了基于GF(2)上本原多项式生成的密钥的密钥长度。我们可以清楚地看到,随着次数的增加,密钥长度也随之增加。当随机选择次数为20 时,生成的密钥的密钥长度为809位。攻击者将尝试 2⁸⁰⁹种可能性来寻找密钥,其成功概率为 $ \frac{1}{2^{809}} $,可以忽略不计。
在生成密钥值后,需要使用以下三个准则对生成的密钥进行随机性测试:标准差、卡方检验、R方检验。执行随机性测试的实验设置如图3所示。
将所提出方法生成的密钥值作为输入提供给标准的伪随机数生成器算法,例如布拉姆·布拉姆·舒布、MT19937,
米卡利‐施诺尔。结果包含了针对0和1的n位计数值的卡方值、R平方值和标准差。其次,我们为相应算法提供了标准输入作为输入。基于上述三个准则,对获得的结果在n位计数值方面进行了比较。本文中,我们考虑了n=2,3,4,8的情况。其中,2位计数值表示生成的密钥中组合00,01,10,11的频率分布。类似地,当使用n=3,4,8时,可以得到不同的组合集合。我们使用以下伪随机数生成器进行了随机性测试:布拉姆‐布拉姆‐舒布(BBS)、MT19937、米卡利‐施诺尔。这些伪随机数生成器(PRNG)如下所述:

布拉姆‐布拉姆‐舒布(BBS)
BBS 是一种安全的伪随机数生成器,可用公式(5)表示:
$$
x_{n+1} \equiv x_n^2 \mod M \tag{5}
$$
其中 $ x_{n+1} $ 表示位奇偶性。M 是两个大素数 p 和 q 的乘积。种子 $ x_0 $ 应选取使得 $ x_0 $ 与 M 的最大公约数为 1,即与 M 互素。BBS 的安全性在 [15] 中通过每次迭代提取 O(n log M)位进行讨论,其中 M 是模数(一个 Blum 整数)。
MT19937[12]
它也被称为梅森旋转伪随机数生成器。该算法的周期长度为梅森素数,即 $ 2^{19937} - 1 $。它的高阶均匀分布优于其他任何伪随机数生成器。尽管依赖于系统,但它已被证明比 rand() 更快。该算法高效利用内存,仅消耗 624个字的工作区。
米卡利‐施诺尔 [13]
这是对RSA伪随机比特生成器的一种改进,证明具有更高的效率和密码学安全性。考虑任意随机 r位序列的 $ x^e \mod n $ 的分布,该分布在区间[0,n −1]内的整数均匀分布中,无法通过所有多项式统计测试加以区分。
生成的密钥的随机性测试基于如下所述的三个标准进行:
Standard Deviation[16]
它是一种用于确定一组数据值的变异或离散度的度量。当数据点更接近数据集的均值时,标准差被称为较低;而高标准差则表明数据点在更广泛的数值范围内更加分散。生成的密钥具有低离散值意味着高随机性。
卡方检验 [17]
它是一种统计假设检验,通常由平方误差和构成。用于确定期望频数与观测频数之间是否存在显著差异。检验值越低,密钥的随机性越高。
R² test[18]
它是一个度量,可提供有关模型拟合优度的信息。可通过使用以下公式计算:
$$
R^2 = 1 - \frac{SS_{res}}{SS_{tot}} \tag{6}
$$
其中 $ SS_{tot} $ 是总平方和,$ SS_{res} $ 是残差平方和。 $ R^2 $ 的值介于 0 和 1 之间。 $ R^2 $ 的值越接近 1,意味着生成的密钥具有更高的随机性。
我们的结果与BBS随机化算法的比较如表1和2所示。表1展示了使用2位、 3位、4位和8位频率分布测试框架,将我们的数据与BBS算法生成的随机值相比的离散度、拟合度和错误率。表2中获得了仅以BBS算法输出的随机值进行类似度量的结果。
一种基于GF(2)上本原多项式的随机密钥生成方案
表1. 由GF(2)上的本原多项式生成的密钥长度
| 次数(n) | 本原多项式数量 | 密钥长度(位) |
|---|---|---|
| 2 | 1 | 150 |
| 3 | 2 | 172 |
| 4 | 2 | 194 |
| 5 | 6 | 203 |
| 6 | 6 | 243 |
| 7 | 18 | 283 |
| 8 | 16 | 324 |
| 9 | 48 | 374 |
| 10 | 60 | 405 |
| 11 | 176 | 445 |
| 12 | 144 | 487 |
| 13 | 630 | 526 |
| 14 | 756 | 570 |
| 15 | 1800 | 607 |
| 16 | 2048 | 647 |
| 17 | 7710 | 680 |
| 18 | 7776 | 728 |
| 19 | 27594 | 755 |
| 20 | 24000 | 809 |
表2. BBS以提出的算法生成的密钥作为输入
| 2 位 | 3 位 | 4 位 | 8 位 | |
|---|---|---|---|---|
| 标准差(%) | 0.2949 | 0.3761 | 0.9217 | 6.2631 |
| R平方值 | 0.9998 | 0.9174 | 0.9894 | 0.9989 |
| 卡方值 | 2.2791 | 2.4725 | 11.1360 | 257.0781 |
表3. BBS与标准输入
| 2 位 | 3 位 | 4 位 | 8 位 | |
|---|---|---|---|---|
| 标准差(%) | 0.3680 | 0.5942 | 1.1028 | 6.0113 |
| R平方值 | 0.9787 | 0.9021 | 0.9751 | 0.9961 |
| 卡方值 | 3.5495 | 6.1698 | 15.9404 | 236.8203 |
表4. Micali‐Schnorr 使用提出的算法生成的密钥作为输入
| 2 位 | 3 位 | 4 位 | 8 位 | |
|---|---|---|---|---|
| 标准差(%) | 0.1127 | 0.5677 | 0.9824 | 6.2727 |
| R平方值 | 0.9242 | 0.9668 | 0.9684 | 0.9985 |
| 卡方值 | 6.3329 | 5.6324 | 12.6504 | 257.8594 |
表5. 米卡利‐施诺尔与标准输入
| 2 位 | 3 位 | 4 位 | 8 位 | |
|---|---|---|---|---|
| 标准差(%) | 0.5031 | 0.5969 | 1.0109 | 6.8131 |
| R平方值 | 0.7392 | 0.9289 | 0.9836 | 0.9970 |
| 卡方值 | 6.6356 | 6.2271 | 13.3938 | 304.2031 |
表6. 使用提出算法生成的密钥作为输入的梅森旋转算法
| 2 位 | 3 位 | 4 位 | 8 位 | |
|---|---|---|---|---|
| 标准差(%) | 0.2367 | 0.5802 | 1.0906 | 6.0909 |
| R平方值 | 0.8889 | 0.9476 | 0.9282 | 0.9992 |
| 卡方值 | 1.4689 | 5.8836 | 15.5908 | 244.9453 |
表7. Mersenne 拧转器与标准输入
| 2 位 | 3 位 | 4 位 | 8 位 | |
|---|---|---|---|---|
| 标准差(%) | 0.2797 | 0.5975 | 1.1393 | 6.1136 |
| R平方值 | 0.7175 | 0.9448 | 0.9280 | 0.9992 |
| 卡方值 | 2.0503 | 6.2381 | 17.0137 | 243.1328 |
当使用生成的密钥作为输入时(如表2所示),2位计数、3位计数和4位计数的离散度(标准差)值小于表3中的离散度值。对于所有这三个计数,表2中的R平方值高于表3,并且除8位计数值外,表2中所有值的卡方值均较小。现在考虑使用米卡利‐施诺尔算法进行随机性测试。表4展示了我们将提出的算法生成的密钥作为输入提供给米卡利‐施诺尔算法时获得的结果。表5中的标准差值小于表4中的标准差值,后者表示向米卡利‐施诺尔算法提供标准输入时的度量结果。
R平方值越接近1,拟合优度就越高。所有R平方值证明生成的密钥是随机的,除了4位计数外。所有卡方值均支持生成的密钥的随机性,因为表4的卡方值相较于表5的卡方值更小。
表6显示了将我们提出的算法生成的密钥作为输入时的离散度、卡方值和R平方值。当在梅森旋转算法中使用标准输入时,表7显示了类似的度量。除了8位计数的卡方值外,表6中的所有测试值均支持生成的密钥的随机性测试。
我们按照框架中所述执行测试用例,在从提出的算法获得的多个随机输出样本(样本大小至少为10)中进行测试,BBS、Micali‐Schnorr和梅森旋转算法。在对2位、3位、4位和8位测试用例的结果进行分析后,观察到提出的算法在72.5%的测试场景中实现了更低的离散度。类似地,在68.3%的测试结果中实现了更高的拟合优度,在61.6%的测试结果中获得了更低的错误率。
5 总结与结论
本文提出了一种基于GF(2)上本原多项式的随机密钥生成算法。我们结合系统IP的哈希值(使用MD5)和系统时间(以毫秒为单位)来生成随机种子,从而增强了安全性。在所有情况下,生成的密钥均通过了随机性测试。我们将结果与三种现有的伪随机数生成器算法进行了比较,比较指标包括R平方值、卡方值和标准差,以及生成密钥值的位数统计。可以得出结论,使用所提出的算法生成的密钥具有随机性。




















 695
695

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








