02_基于线性回归预测糖尿病

基于线性回归预测糖尿病

1、实验描述

• 使用Python编程，利用diabetes
  dataset，一个糖尿病数据集，主要包括442行数据，10个属性值，分别是：Age(年龄)、性别(Sex)、Body
  mass index(体质指数)、Average Blood
  Pressure(平均血压)、S1~S6一年后疾病级数指标。Target为一年后患疾病的定量指标。首先将数据集划分为训练集和测试集，创建线性回归模型，然后训练数据集，得到每个特征下的参数。绘图表示出真实值和预测值之间的对比。

• 实验时长：35分钟

• 主要步骤：

  • 数据集的划分

  • 创建普通线性回归模型

  • 将训练数据输入学习模型中进行训练

  • 将测试数据输入模型，获得预测结果

  • 绘图进行效果评估

2、实验环境

• 系统版本：CentOS7

• Python版本：3.6.6

• Matplotlib版本：2.2.2

• Anaconda版本：4.3.30

• Numpy版本：1.13.1

• scikit-learn版本：0.18.2

3、相关技能

• Python编程

• 线性回归模型

4、相关知识点

• LinearRegression

  • 是scikit-learn提供的线性回归模型，其原型为：

  • class sklearn.linear_model.LinearRegression(fit_intercept=True,
    normalize=False, copy_X=True, n_jobs=1)

  • 导入：from sklearn.linear_model import LinearRegression

  • 参数

• （1）fit_intercept :
  一个布尔值，指定是否需要计算b值。如果为False，那么不计算b值。

• （2）normalize : 一个布尔值。如果为True，那么训练样本会在回归之前被归一化。

• （3）copy_X : 一个布尔值。如果为True，则会被复制。

• （4）n_jobs :
  一个正数。任务并行时指定的CPU数量。如果为-1则使用所有可用的CPU。

  • 属性

• （1）coef_ : 权重向量。

• （2）intercept_ : 截距b值。

  • 方法

• （1）fit(X,y) : 训练模型。

• （2）predict(X) : 用模型预测，返回预测值。

• （3）score(X,y) : 返回性能得分。设预测集为

>   ,真实值为

>   ，真实值的均值为

>   ,预测值为

>   ，则： 

• 线性回归

  • 在统计学中，线性回归(Linear
    Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。

  • 回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

  • 建立函数模型
    

• 训练数据

• 采用矩阵表示

• 最小二乘法

• 我们有很多的给定点，这时候我们需要找出一条线去拟合它，那么我先假设这个线的方程，然后把数据点代入假设的方程得到观测值，求使得实际值与观测值相减的平方和最小的参数。对变量求偏导联立便可求。

• 表示损失代价函数：
  

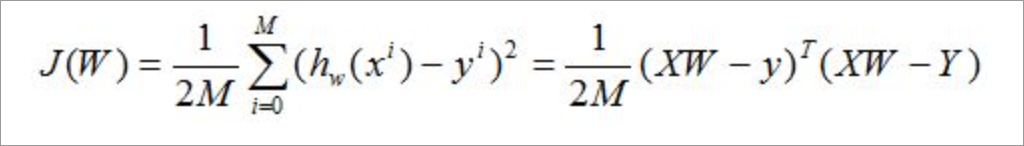
• 求解使得代价函数最小的W

• 矩阵满秩，

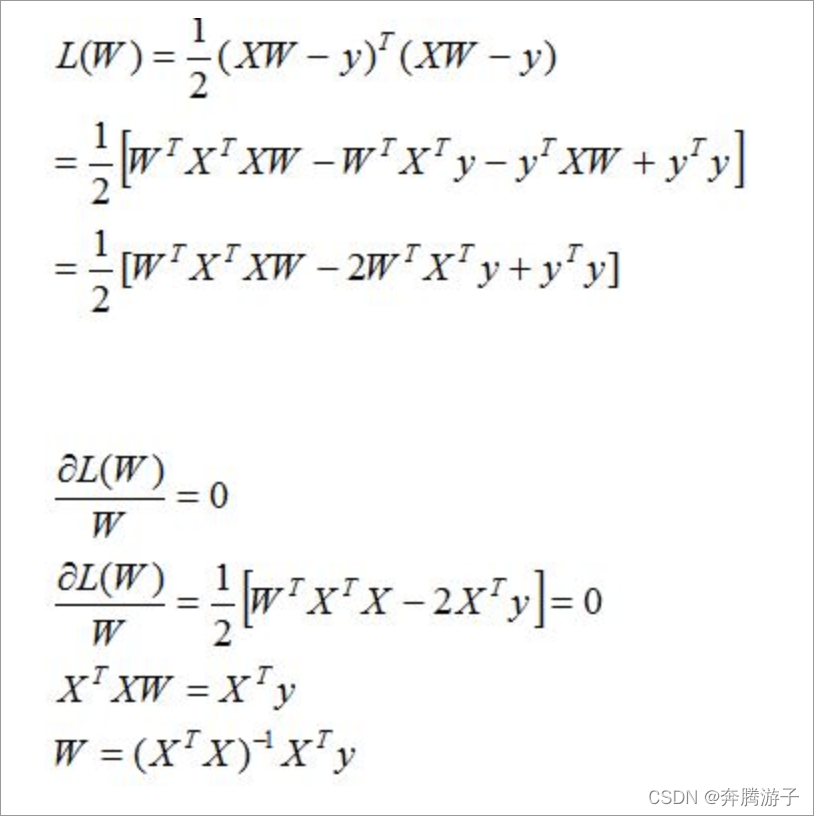
• 矩阵不满秩，采用梯度下降法。梯度下降算法是一种求局部最优解的方法，对于F(x)，在a点的梯度是F(x)增长最快的方向，那么它的相反方向则是该点下降最快的方向。

• 梯度下降法的原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快；注意：当变量之间大小相差很大时，应该先将他们做处理，使得他们的值在同一个范围，这样比较准确。

• 梯度下降法步骤：

1. 首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

2. 改变θ的值，使得J(θ)按梯度下降的方向进行减少。描述一下梯度减少的过程，对于我们的函数J(θ)求偏导J：

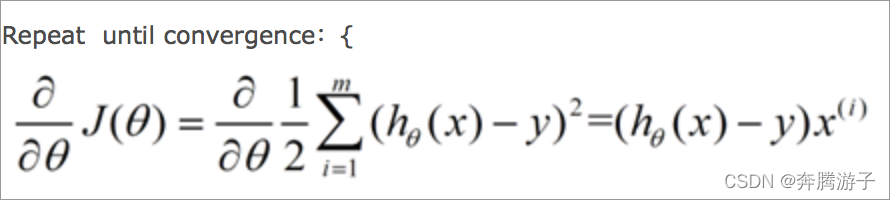
下面是更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

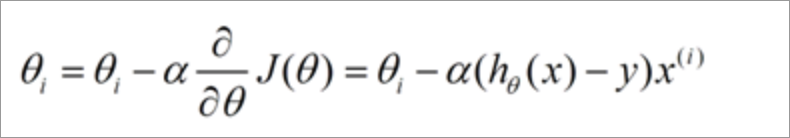
• 假设有数据集D时：

• 对损失函数求偏导如下：

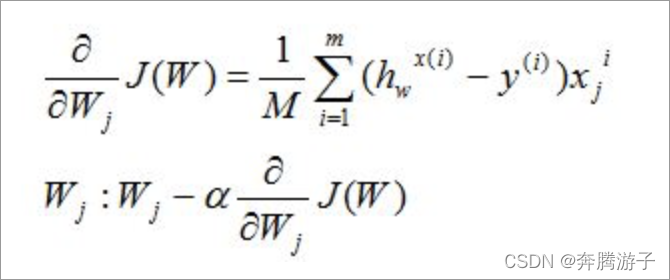
• 使用矩阵表示：

• 从概率层面解释-回归模型的目标函数：

• 中心极限定理：设有n个随机变量，X1,X2,X3,Xn,他们之间相互独立，并且有相同的数学期望和均值。E(X)=u;
  D(x)=δ2.令Yn为这n个随机变量之和。
  

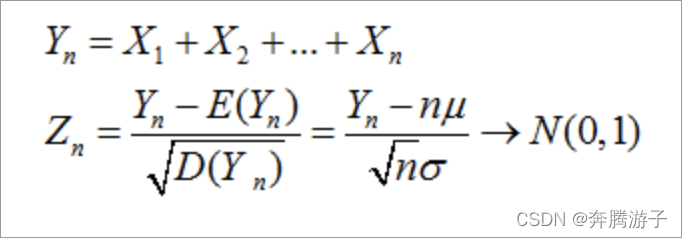
Zn为X这几个变量的规范和。

• 高斯分布：假的给定一个输入样本x，我们得到预测值和真实值间的存在的误差e，那么他们的关系如下：
  

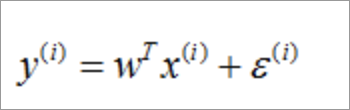
• 假设e服从标准的高斯分布。

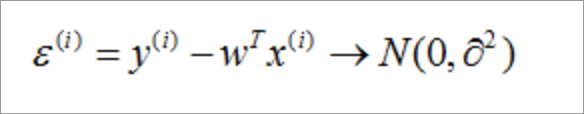
• 那么x和y的条件概率：
  

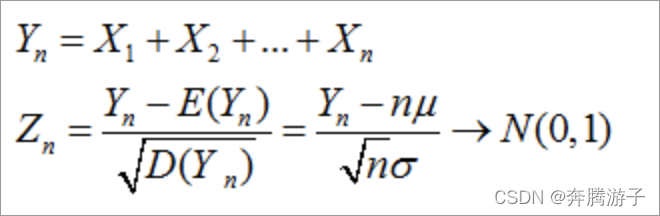
• 那么知道一条样本的概率，我们就可以通过极大估计求似然函数，优化的目标函数如下：
  

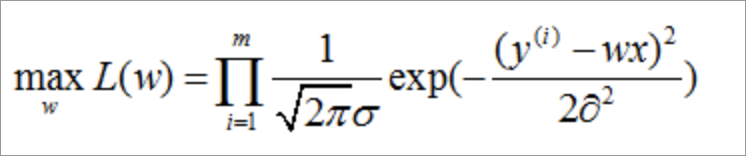
• 通过取对数我们可以发现极大似然估计的目标函数和最小平方误差是一样。在概率模型中，目标函数的极大和极小与极大似然估计是等价的。

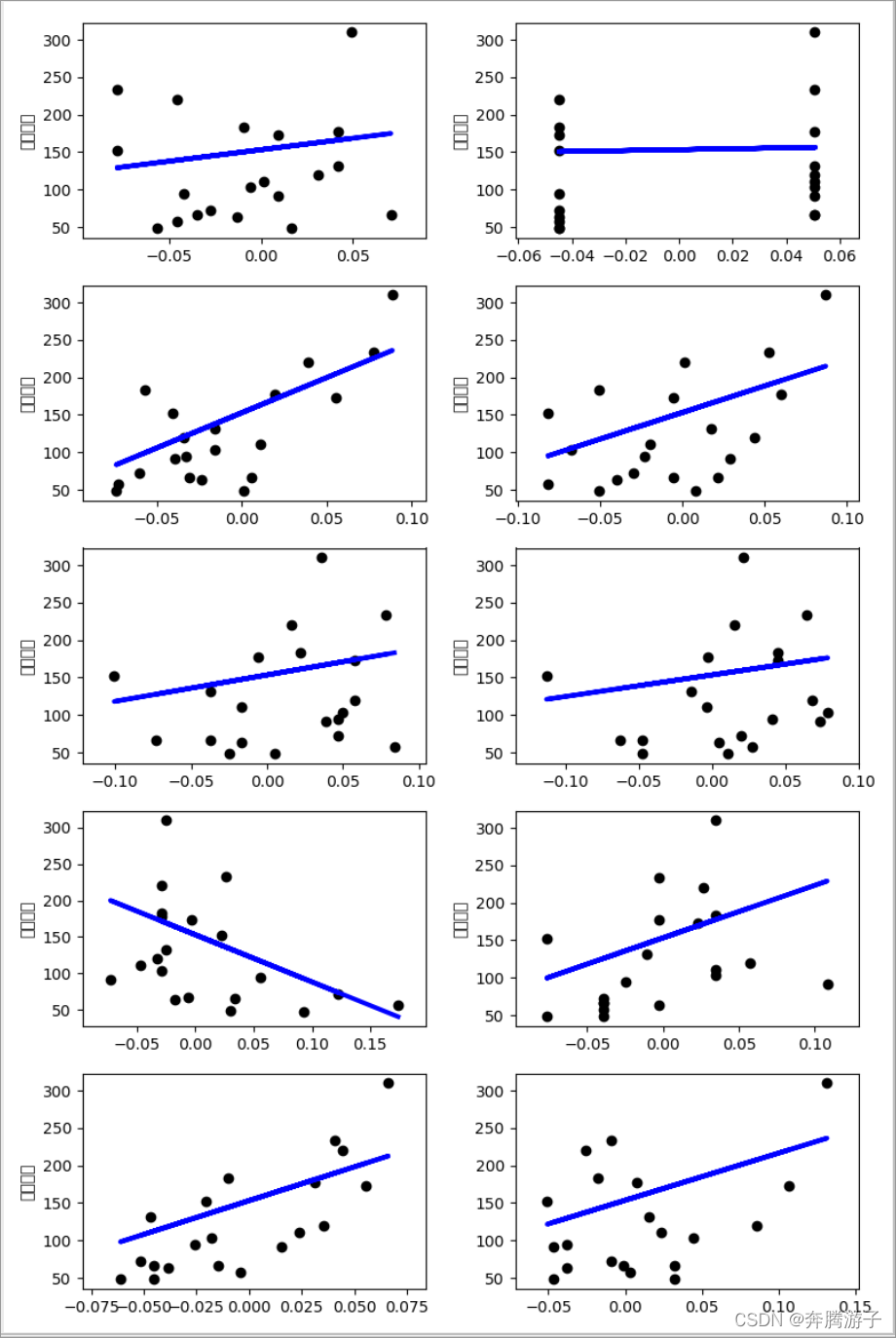
5、实现效果

• 结果如下图：
  

图 1

6、实验步骤

6.1数据集参考http://scikit-learn.org/stable/datasets/。在本次实验中，我们使用sklearn.datasets
包，该包提供了一些小的toy数据集。为了评估数据特征(n_samples,n_features)的影响,可以控制数据的一些统计学特性，产生人工数据。这个包提供一些接口，来获取真实的机器学习社区常用于基准算法的大数据集。数据集已下载并存放于/home/zkpk/experiment/experiment2目录下。

图 2

进入/home/zkpk/pycharm-2017.3.5/bin目录，切换到root用户，输入密码（zkpk）

[zkpk@localhost tgz]$ cd ~/pycharm-2017.3.5/bin
[zkpk@localhost bin]$ su root

图 3

修改hosts文件，在/etc/hosts文件末添加一行0.0.0.0
account.jetbrains.com，注意account前面有一个空格（按I键，添加以下内容后按Esc键，输入:wq，再按Enter键即可保存退出）。修改完成后使用exit命令退出root权限。

[root@localhost bin]# vi /etc/hosts
0.0.0.0 account.jetbrains.com

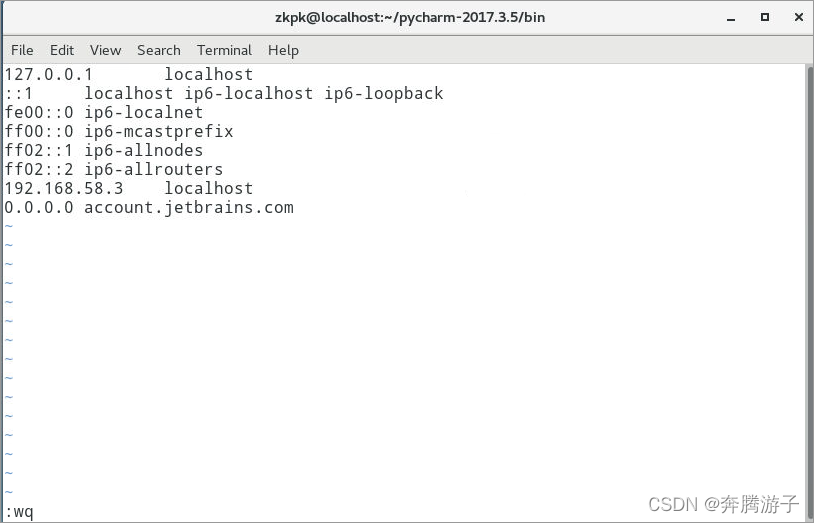
6.2在/home/zkpk/pycharm-2017.3.5/bin目录下，使用./pycharm.sh命令打开Pycharm,
点击open打开工程LR，在工程下创建lr_diabetes.py并设置Python Interpreter。

图 3

图 4  图 5  图 6

6.3Import相关工具包。

import numpy as np
from sklearn import datasets
from sklearn import linear_model
import matplotlib.pyplot as plt

图 7

6.4获取数据集

diabetes = datasets.load_diabetes()
# 查看第一列年龄的数据
print(diabetes.data[0])
# 求证： 每一列的数值的平方和为1
print(np.sum(diabetes.data[:, 0] ** 2))
# 求年龄列
# 糖尿病进展的数据
print(diabetes.target)
# 数值介于   25到346之间

图 8

6.5切分训练集与测试集

x_train = diabetes.data[:-20]
y_train = diabetes.target[:-20]
x_test = diabetes.data[-20:]
y_test = diabetes.target[-20:]

图 9

6.6创建线性回归模型，用训练集训练模型

# 创建线性回归
linreg = linear_model.LinearRegression()
# 用训练集训练模型
linreg.fit(x_train, y_train)
# 调用预测模型的coef_属性,求出每种生理数据的回归系数b, 一共10个结果，分别对应10个生理特征.
print(linreg.coef_)

图 10

6.7查看预测值和实际目标值

# 在模型上调用predict()函数，传入测试集，得到预测值，
print(linreg.predict(x_test))
# 结果:array([ 197.61846908,  155.43979328,  172.88665147,  111.53537279,
#      164.80054784,  131.06954875,  259.12237761,  100.47935157,
#      117.0601052 ,  124.30503555,  218.36632793,   61.19831284,
#      132.25046751,  120.3332925 ,   52.54458691,  194.03798088,
#      102.57139702,  123.56604987,  211.0346317 ,   52.60335674])


# 查看实际目标值
print(y_test)
# 结果：array([ 233.,   91.,  111.,  152.,  120.,   67.,  310.,   94.,  183.,
#         66.,  173.,   72.,   49.,   64.,   48.,  178.,  104.,  132.,
#        220.,   57.])
linreg.score(x_test, y_test)

图 11

6.8对每个特征值绘制一个线性回归图

plt.figure(figsize=(8, 12))
# 循环10个特征h
for f in range(0, 10):
    # 取出测试集中第f特征列的值, 这样取出来的数组变成一维的了，
    xi_test = x_test[:, f]
    # 取出训练集中第f特征列的值
    xi_train = x_train[:, f]

    # 将一维数组转为二维的
    xi_test = xi_test[:, np.newaxis]
    xi_train = xi_train[:, np.newaxis]

    plt.ylabel(u'病情数值')
    linreg.fit(xi_train, y_train)  # 根据第f特征列进行训练
    y = linreg.predict(xi_test)  # 根据上面训练的模型进行预测,得到预测结果y

    # 加入子图
    plt.subplot(5, 2, f + 1)  # 5表示10个图分为5行, 2表示每行2个图, f+1表示图的编号，可以使用这个编号控制这个图
    # 绘制点   代表测试集的数据分布情况
    plt.scatter(xi_test, y_test, color='k')
    # 绘制线
    plt.plot(xi_test, y, color='b', linewidth=3)

plt.savefig('python_糖尿病数据集_预测病情_线性回归_最小平方回归.png')
plt.show()

图 12

6.9右键点击‘run ‘lr_diabetes’运行程序。

图 13

6.10个特征的线性回归图绘制结果如下图：

图 14

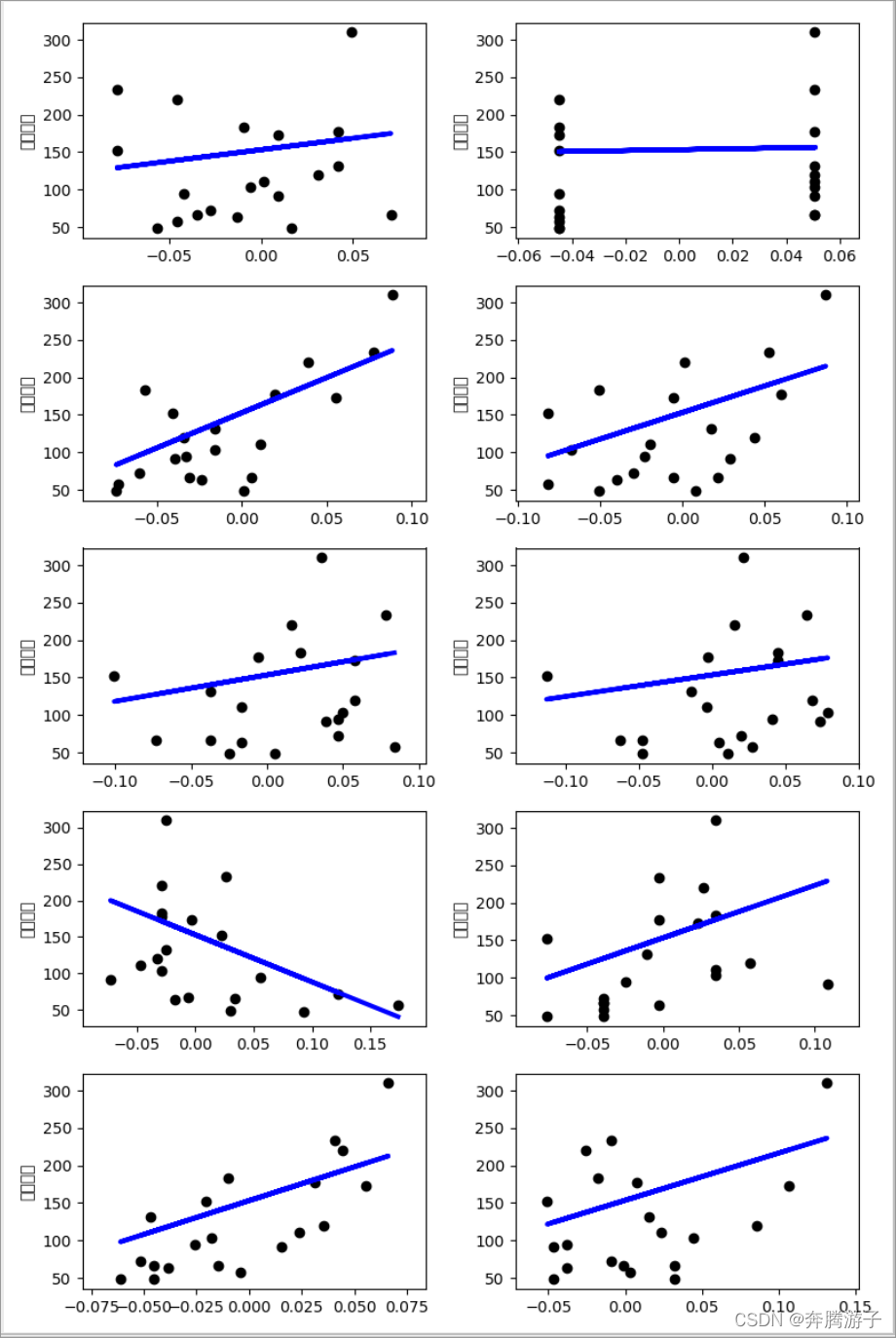
7、参考答案

• 代码清单LR. lr_diabetes.py

图 15  图 16

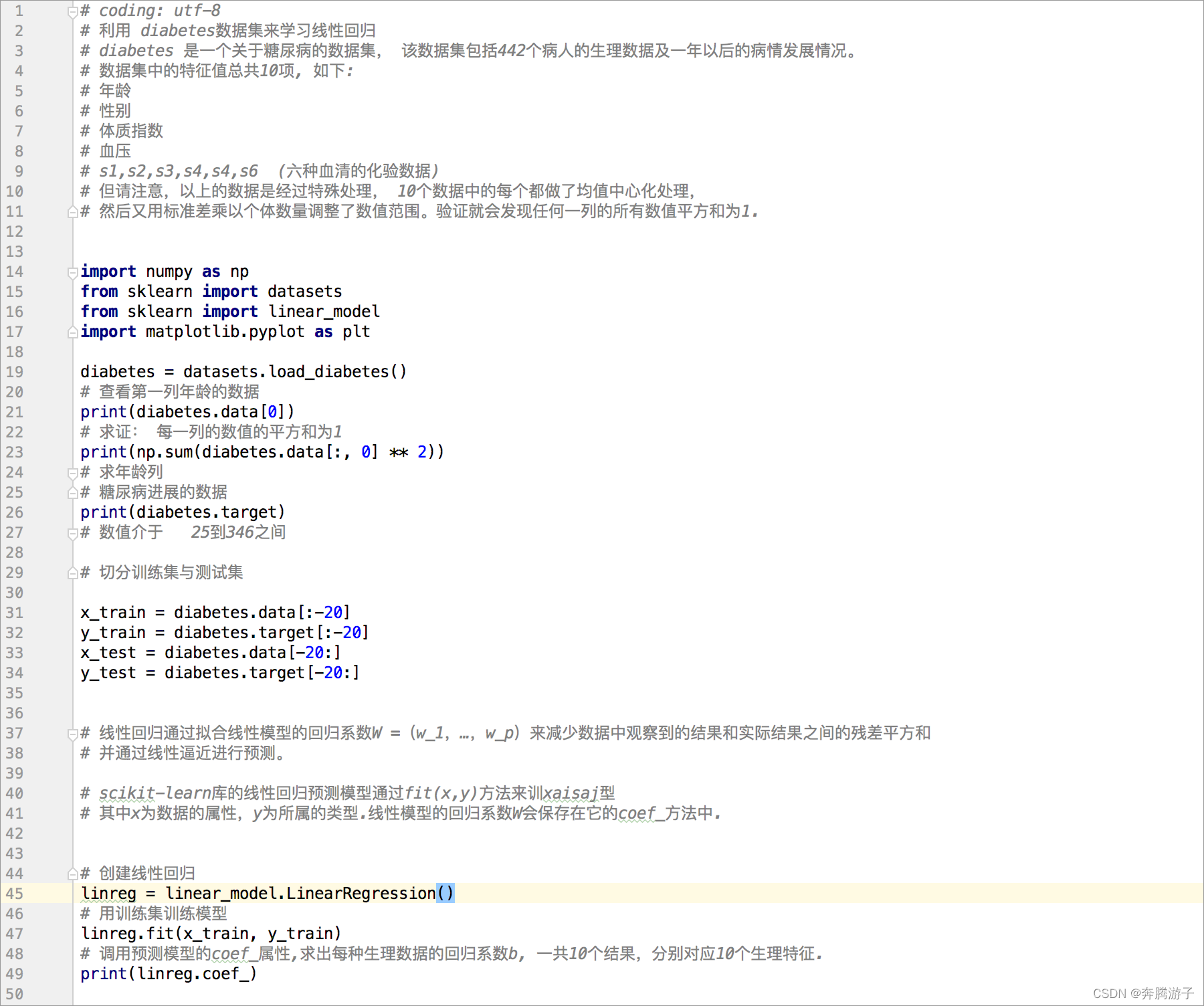
8、总结

完成本实验可掌握线性回归的原理以及一元线性回归的实现，并且学会使用SciKit
learn实现回归算法，以及使用SKlearn的强大数据库。