我们初高中学过波可以发生衍射,但是当时并没有讲原理,而是把衍射当波的特性。这几天偶然看到了有人讲量子的波动性,我就又想要了解清楚为啥波会衍射。为此查了一些资料,可以用惠更斯原理解释水波的衍射现象
从波源发出的波经过同一传播时间到达的各点所组成的面,叫做波面(或波前)(以水波这个二维平面波为例,就是那些涟漪,也就是一圈圈的波纹,同一圈的水(分子)构成的弧面或者弧线,就是波面了).荷兰物理学家惠更斯经过长期研究,于1690年提出了一条关于波的传播的重要原理,叫做惠更斯原理,这一原理是:波面上的各点可以看做是新的波源,叫做子波源.从这些子波源发出的子波所形成的包面(或包迹),就是下一时刻的新的波面.
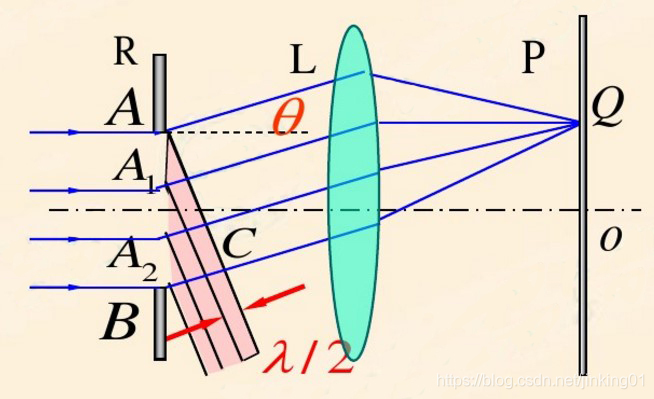
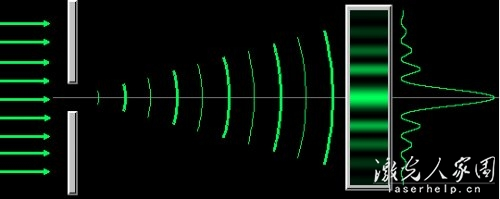
用惠更斯原理很容易说明水波通过障碍物的缝时的衍射现象.设波阵面为直线形的水波,到达障碍物的缝时,缝上各点成为新的子波源.以这些子波源为中心作半径为vt(v为波速)的半圆面,再作与半圆面相切的包面,这个包面就是波通过缝后在时刻t的波面.从图中可以看出,直线形水波通过缝后,除与缝的宽度相等部分的波面仍为直线外,在缝的边缘处,波面的相当大的一部分发生了弯曲,传播到了障碍物的后面,这就是衍射现象.
当缝的大小(或障碍物的大小)跟波长相差不多时就发生明显的衍射现象.如果缝很宽,其宽度远大于波长,则波通过缝后基本上是沿直线传播的,衍射现象就很不明显了.
用惠更斯原理虽然能定性地解释衍射现象,但不能对衍射现象作出定量的分析.19世纪初法国物理学家菲涅耳补充了惠更斯原理,他认为任一时刻的波面并不是简单地由子波的包迹形成的,而是它们互相干涉的结果.经过这样补充的惠更斯-菲涅耳原理,能够确切地解释波的衍射现象.





















 1510
1510

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








