J - 食物链 POJ - 1182

最新推荐文章于 2025-05-23 08:55:07 发布

jikelk

最新推荐文章于 2025-05-23 08:55:07 发布

阅读量399

点赞数 2

分类专栏： c++ 文章标签：算法图论 c++

本文链接：https://blog.youkuaiyun.com/jikelk/article/details/128267066

版权

c++ 专栏收录该内容

85 篇文章

订阅专栏

思路：

首先我们要理清楚三种动物之间的关系，那么可以用A到B的距离为1代表为A吃B，

那么就有下图的关系

那么我们用d=1表示吃，d=2表示被吃，d=3表示是同类

对于另一张图也是符合的

然后我们去找每个点和他的根节点的关系

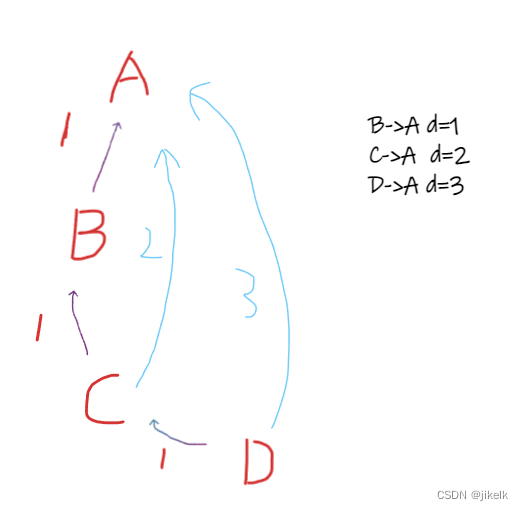
那么对于每个点和根节点的关系，就是它的d对应的关系（如C->A，d=2，那么C被A吃）

然后我们去推导任意两个点的关系（通过根节点）

B到根节点的d是1，C到根节点的d是2，那么C和B的关系是2-1=1，即C吃B;

如果是D和B的关系也一样：B到根节点的d是1，D到根节点的关系是3，那么关系是3-1=2，于是D（A）被B吃。

我们可以发现，X动物到Y动物到根节点的关系相减如果%3是1的话，就是X吃Y，如果%3为2的话，就是X被Y吃，如果%3为0的话，那么就是同类的关系。

那么对于D=1的情况

先找到x和y的头节点tx和ty。

如果tx不等于ty（即不在一个集合中），那么就不存在错误的可能，就把他们两个加入到一起中，

（p[tx]=ty）并且要满足 $(d[x]+d[tx])%3=d[y]%3$ ，那么 $d[tx]=(d[y]-d[x]+3)%3$

如果tx==ty，那么就说明这两个动物已经存在了一种关系，就判断一下两个动物到根节点的值的差%3是不是0就可以了

如果D=2

一样也是先找到x和y的头节点tx,ty

如果tx不等于ty（即不在一个集合中），那么就不存在错误的可能，就把他们两个加入到一起中，

（p[tx]=ty）并且要满足 $(d[x]+d[tx]-d[y])%3=1$ ,那么 $d[tx]=(d[y]-d[x]-1+3)%3$

如果tx==ty，那么就说明这两个动物已经存在了一种关系，就判断一下两个动物到根节点的值的差%3是不是1就可以了（图画的有点丑咳咳）

对于find函数：

因为是要找到他的根节点，并且要在找根节点的途中去更新他到根节点的距离

那么可以通过调用递归函数先算出根节点，然后通过根节点的d去更新后面的d。

if (p[x] != x)

{

int t = find(p[x]);

d[x] += d[p[x]];

d[x] %= 3;

p[x] = t;

}

return p[x];

代码：

/**
 *　　┏┓　　　┏┓+ +
 *　┏┛┻━━━┛┻┓ + +
 *　┃　　　　　　　┃
 *　┃　　　━　　　┃ ++ + + +
 *  ████━████+
 *  ◥██◤　◥██◤ +
 *　┃　　　┻　　　┃
 *　┃　　　　　　　┃ + +
 *　┗━┓　　　┏━┛
 *　　　┃　　　┃ + + + +Code is far away from 　
 *　　　┃　　　┃ + bug with the animal protecting
 *　　　┃　 　 ┗━━━┓ 神兽保佑,代码无bug　
 *　　　┃ 　	　　　 ┣┓
 *　　  ┃ 　　　　　 　┏┛
 *　    ┗┓┓┏━┳┓┏┛ + + + +
 *　　　　┃┫┫　┃┫┫
 *　　　　┗┻┛　┗┻┛+ + + +
 */

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
#define sc_int(x) scanf("%d", &x)
#define sc_ll(x) scanf("%lld", &x)
#define pr_ll(x) printf("%lld", x)
#define pr_ll_n(x) printf("%lld\n", x)
#define pr_int_n(x) printf("%d\n", x)
#define ll long long
using namespace std;

const int N = 1000000 + 100;
int n, m, h;
int p[N], d[N];

int find(int x)
{
	if (p[x] != x)
	{
		int t = find(p[x]);
		d[x] += d[p[x]];
		d[x] %= 3;
		p[x] = t;
	}
	return p[x];
}

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		p[i] = i;

	int res = 0;
	while (m--)
	{
		int x, y;
		sc_int(h),sc_int(x),sc_int(y);
		if (x > n || x < 1 || y > n || y < 1 || (x == y&&h==2))
		{
			res++;
			continue;
		}
		int hx = find(x), hy = find(y);
		if (h == 1)
		{
			if (hx == hy && ((d[x] - d[y] + 3) % 3))
				res++; // 根节点相同并且到根节点的距离不一样
			else if (hx != hy)
			{
				p[hx] = hy;
				d[hx] = (d[y] - d[x] + 3) % 3;
			}
		}
		else
		{
			if (hx == hy && (d[x] - d[y] + 3) % 3 != 1)
				res++;
			else if (hx != hy)
			{
				p[hx] = hy;
				d[hx] = (d[y] - d[x] + 1 + 3) % 3;
			}
		}
	}
	cout << res << endl;

	return 0;
}

ending：咳咳，因为自己是个蒻蒻，所以写题解肯定是没有其他大佬写的好，就当是分享自己的思路了？希望有所帮助吧~