nyist 第二次招新赛 I 董学姐与朱学姐的爱恨情仇

董学姐与朱学姐的爱恨情仇。 - NYOJ

 

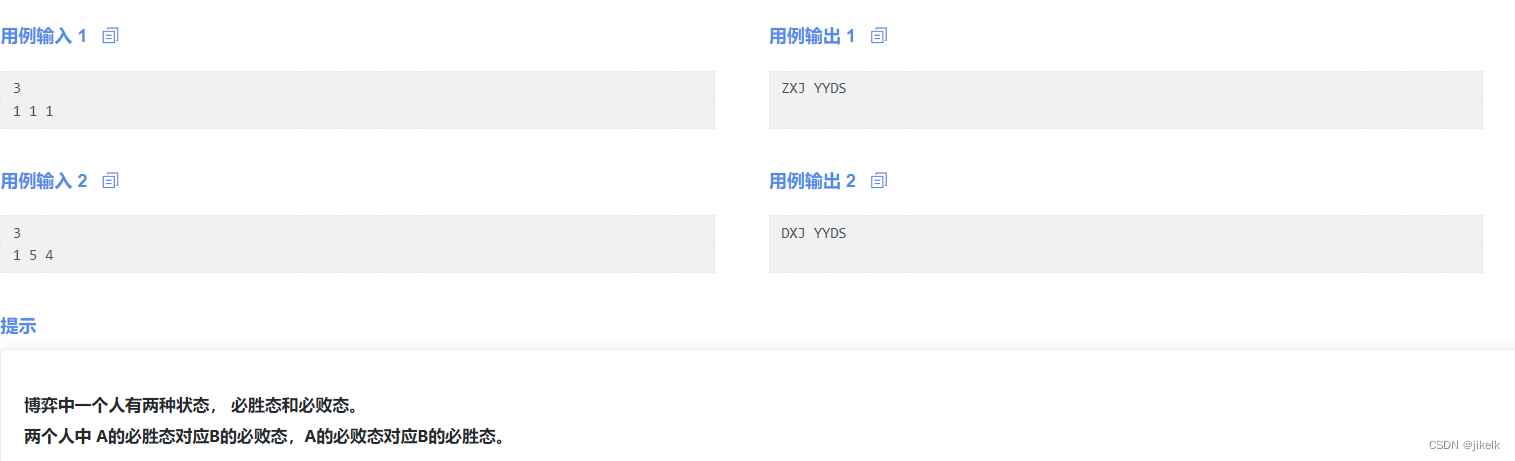
 思路：  首先我们可以假定朱学姐一定是赢的，那么我们要保证朱学姐一定是第一个拿到最后一堆的，那么我们就考虑在前n个石头之后朱学姐能不能继续保持先手。

首先，如果每个石头堆里面都大于等于2，那么朱学姐一定可以通过拿一堆的数-1来控制朱学姐的先手从而使朱学姐win！

那么再分析有1的情况

那么对于第一个数为1的情况，那么一定会造成先手的强制转换：如果不是1，

那么可以分情况讨论（因为为1的话一定会造成先手的强制转换）

假设此时朱学姐先手：

如果是 4 1 ，那么此时朱学姐全拿，董学姐拿第二堆，最后朱学姐还是先手。

如果是 4 1 1 ，那么朱学姐可以拿3个，后面董学姐拿第一堆的剩下一个，然后朱学姐拿第二堆，董学姐拿第三堆，最后朱学姐还是先手。

那么我们可以发现，对于第一个数不是1，第二个数是一的情况，我们可以通过操作（因为要优）使先手不改变。那么规律就找好了。

/**
*　　┏┓　　　┏┓+ +
*　┏┛┻━━━┛┻┓ + +
*　┃　　　　　　　┃
*　┃　　　━　　　┃ ++ + + +
*  ████━████+
*  ◥██◤　◥██◤ +
*　┃　　　┻　　　┃
*　┃　　　　　　　┃ + +
*　┗━┓　　　┏━┛
*　　　┃　　　┃ + + + +Code is far away from 　
*　　　┃　　　┃ + bug with the animal protecting
*　　　┃　 　 ┗━━━┓ 神兽保佑,代码无bug　
*　　　┃ 　	　　　 ┣┓
*　　  ┃ 　　　　　 　┏┛
*　    ┗┓┓┏━┳┓┏┛ + + + +
*　　　　┃┫┫　┃┫┫
*　　　　┗┻┛　┗┻┛+ + + +
*/

#include<cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include<vector>
#include<queue>
#include<map>
#define sc_int(x) scanf("%d", &x)
#define sc_ll(x) scanf("%lld", &x)
#define pr_ll(x) printf("%lld", x)
#define pr_ll_n(x) printf("%lld\n", x)
#define pr_int_n(x) printf("%d\n", x)
#define ll long long 
using namespace std;

const int N=1000000+100;
int n ,m,h;
ll s[N];



int main()
{
	int t;
	sc_int(t);
	bool flag=0;
	for(int i =1;i<=t;i++)
	{
		sc_int(s[i]);
		if(s[i]==1)flag=1;
	}
	if(!flag)cout<<"ZXJ YYDS\n";
	else {
		int first=1;//1代表朱，0代表董
		for(int i =1;i<=t-1;i++)
		{
			if(s[i]==1){
				first=1-first;
			}
			else while(s[i+1]==1&&i+1<=t-1)
			i++;
		}
		if(first)
		cout<<"ZXJ YYDS\n";
		else 
		cout<<"DXJ YYDS\n";
	}
	return 0;
}