今天我们学做一下NC文章的小提琴图,有小提琴图,也有散点,其实看过之前系列文章的人如果能够联想,可以想到这个的结合。只不过这篇文章的图有个特点是散点分布和小提琴图形状一致,在画散点的时候利用geom_quasirandom 代替geom_jitter即可。

image.png
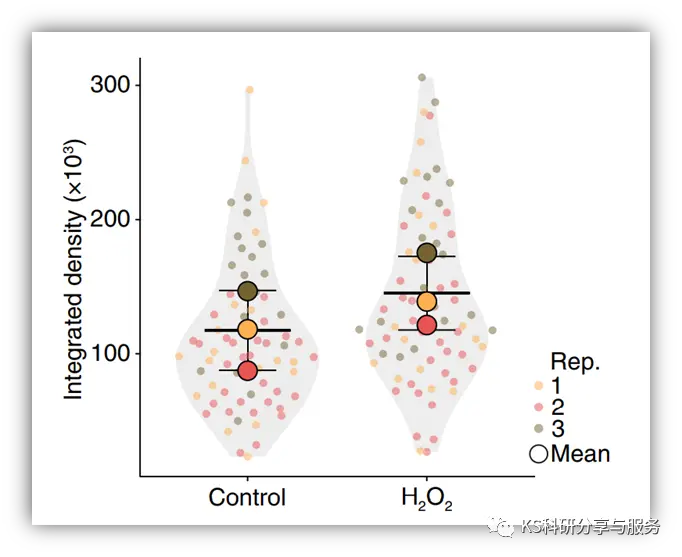
image.png
原文提供了原始作图数据,可去官网下载。
示例数据和注释代码已上传群文件,免费获取可加群!
作图:
读入数据
setwd("D:/KS项目/复现NC")
A <- read.csv("Fig3f.csv", header = T)
A$Integrated.density <- 0.001*A$Integrated.density
library(ggplot2)
library(ggbeeswarm)
library(ggpubr)
A$Biological.replicate <- as.factor(A$Biological.replicate)
计算平均值、sd等:
library(dplyr)
B <- A %>%
group_by(Treatment) %>%
mutate(upper = quantile(Integrated.density, 0.75),
lower = quantile(Integrated.density, 0.25),
mean = mean(Integrated.density),
median = median(Integrated.density),
sd = sd(Integrated.density))
ggplot作图:
ggplot(A,aes(x=Treatment,y=Integrated.density))+
geom_violin(width =0.8,fill='#EDEDED',color='#EDEDED')+
geom_quasirandom(aes(color=Biological.replicate),width = 0.4,size=2.5)+
scale_color_manual(name = 'Rep.',
values = c('#FFD7A8','#F2A9A9','#BAB099'),
labels = c('1','2','3'))+
theme_classic()+
labs(x=" ",
y=expression('Integrated density (x'~10^3~')'))+
theme(axis.title.y = element_text(colour = 'black',size = 16),
axis.text = element_text(colour = 'black',size = 14),
axis.line = element_line(size = 1),
legend.title = element_text(size = 14),
legend.text = element_text(size = 14))+
guides(color=guide_legend(override.aes = list(size=4)))+
geom_errorbar(data=B, aes(ymin = mean-sd,
ymax = mean+sd),width = 0.2,size=0.5)+
stat_summary(fun = "mean",
geom = "crossbar",
mapping = aes(ymin=..y..,ymax=..y..),
width=0.4,
size=0.3)+
stat_summary(aes(fill=Biological.replicate), geom="point",
fun = mean, shape=21, size=6,stroke=1.3)+
scale_fill_manual(values = c('#FFAF51','#E65454','#756233'))+
geom_signif(data=A,
aes(xmin=1, xmax=2, annotations="0.3008367",
y_position=310),
textsize = 5,tip_length = c(0, 0),
manual=TRUE, size = 0.5)+
guides(fill=guide_legend(title = 'Mean'))
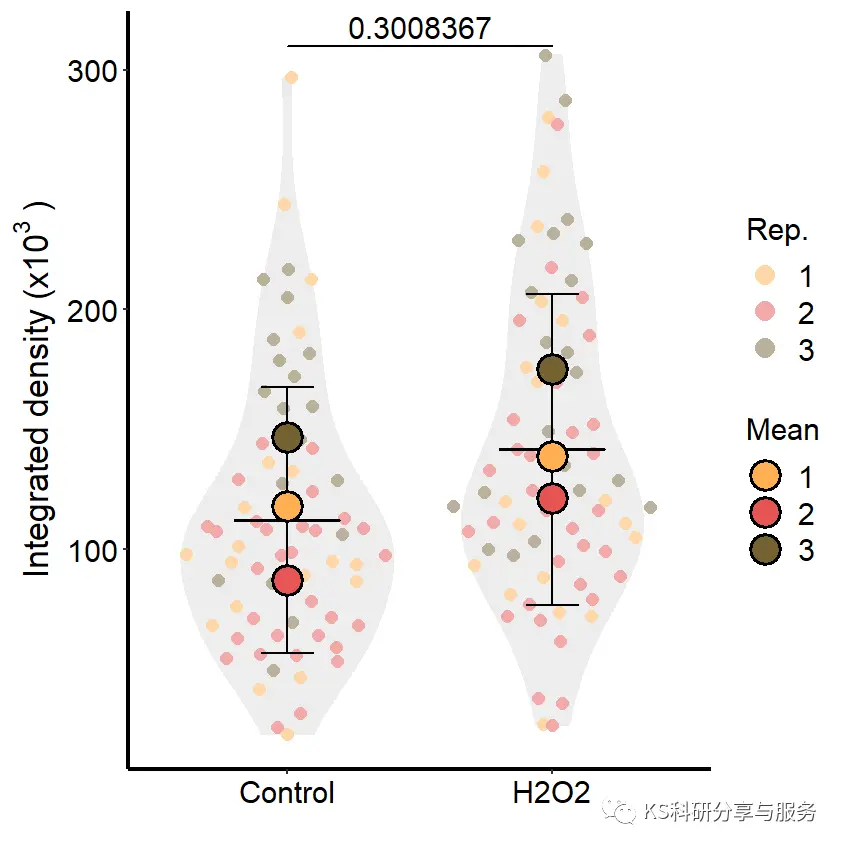
image.png
结果基本是一致的,不同之处在于误差线,我是按照mean±sd,和原文有出入。其次Mean的图例,这里没有修改,不知有啥好办法,原文只有一个圈,其实用annotate函数可以加上。
更多精彩请关注我的公众号《KS科研分享与服务》
AI大模型学习福利
作为一名热心肠的互联网老兵,我决定把宝贵的AI知识分享给大家。 至于能学习到多少就看你的学习毅力和能力了 。我已将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。
一、全套AGI大模型学习路线
AI大模型时代的学习之旅:从基础到前沿,掌握人工智能的核心技能!

因篇幅有限,仅展示部分资料,需要点击文章最下方名片即可前往获取
二、640套AI大模型报告合集
这套包含640份报告的合集,涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师,还是对AI大模型感兴趣的爱好者,这套报告合集都将为您提供宝贵的信息和启示。

因篇幅有限,仅展示部分资料,需要点击文章最下方名片即可前往获
三、AI大模型经典PDF籍
随着人工智能技术的飞速发展,AI大模型已经成为了当今科技领域的一大热点。这些大型预训练模型,如GPT-3、BERT、XLNet等,以其强大的语言理解和生成能力,正在改变我们对人工智能的认识。 那以下这些PDF籍就是非常不错的学习资源。

因篇幅有限,仅展示部分资料,需要点击文章最下方名片即可前往获
四、AI大模型商业化落地方案

因篇幅有限,仅展示部分资料,需要点击文章最下方名片即可前往获
作为普通人,入局大模型时代需要持续学习和实践,不断提高自己的技能和认知水平,同时也需要有责任感和伦理意识,为人工智能的健康发展贡献力量





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








