向量数据库超硬核升级！2 种度量空间，1 个算法全搞定！

本文链接：https://blog.youkuaiyun.com/jike007gt/article/details/148434980

向量检索算法，作为 AI 时代基础设施 —— 向量数据库的核心组件，已被广泛应用于各类由 AI 模型驱动的搜索场景中，例如推荐系统召回、搜索引擎召回、以图搜图、语音检索、人脸识别与匹配、RAG（Retrieval-Augmented Generation）等。

然而，深入了解相关研究进展后我们会发现，当前面向最小欧式距离（Minimal Euclidean distance）检索和面向最大内积（Maximum Inner Product）检索的算法之间，存在一条难以跨越的技术鸿沟。这种割裂，正是许多朋友向我吐槽 “向量检索门槛太高” 的根本原因之一。

大多数使用向量数据库的用户，其实并不关心生成向量的 AI 模型是如何训练的，也不太在意该选择什么样的模型架构或向量度量方式 —— 他们只想知道一件事：到底该用哪种算法、哪种度量方式，效果最好？

但当用户去查阅资料或请教研究者时，得到的回答往往是：“这个模型适合用欧式距离”、“那个模型用最大内积效果更好”，甚至进一步细分到图类算法、量化算法、哈希算法…… 算法种类五花八门，度量方式也各有差异，面对动辄上亿级的数据量，用户自然难免感到无从下手：总不能让我一个个算法都试一遍吧？

01 欧式距离量身定制索引

幸运的是，我们在持续的研究探索中，逐渐找到了弥合欧式度量和内积度量鸿沟的 “粘合剂”。

在前不久针对我们 VLDB2025 的新工作 PSP 的介绍中，我们从理论上证明了：一个为欧式距离量身定制的 “索引”（用来存储向量数据的一种数据结构），也可以用非常小的改动，来适应最大内积检索这个目标，但这显然不是针对内积最优化的选择。

我们追求的目标就是，在 “欧式” 到 “内积” 的悬崖间，架起一座桥。

02 方法论

要实现这个目标，难度不小。在设计一种兼容式的向量检索算法之前，我们首先要对齐不同度量空间下，数据结构的拓扑逻辑：我们希望能用一种统一的数据结构实现存储，并且用统一的算法逻辑进行向量检索。总不能像 “瑞士军刀” 一样，切肉的时候取小刀，剪纸的时候切换剪刀，这就成了一个 “工具库”，而不是一个浑然一体的万能钥匙。

从这个角度出发，我们的算法选型定在了图结构索引上，主要有这几个原因：

1）基于图的算法检索速度快，目前在大规模工业应用有得到验证。

2）“图” 的结构易扩展，可以兼容不同的 “选边逻辑”，支持不同的检索模式。

写到这，熟悉这个领域的朋友可能已经猜到我们想干嘛了。没错！我们要构建异构图索引！

03 新的选边策略和 Dominators

以往的图索引算法，从这个角度说，都可以定义为 “同构图”。我们都知道，图的数学表示可以写作 G=(V, E)，V 是点的集合，E 是边的集合。同构图呢，就是在 E 这个集合里只有一种类型的边。而异构图呢，则是可以包含任意多种类型的边。

以往在最小欧式距离检索比较出名的算法，例如 HNSW，NSG，SSG 等，本质上都属于同构图，也就是说 E 里面只有 “为了欧式度量设计” 的边。在最大内积检索领域，基于图的算法的发展速度一直落后于欧式度量的原因，就是没有一个为 “内积度量” 量身定制的选边算法。

我们回顾 HNSW，NSG 的成功，主要归功于下面这个选边算法：

简单理解，这个选边逻辑就是把图结构中所有三角形中的最长边给 “删除” 掉。由此，图类的算法可以为每个点只连接接近 O (log N) 数量的邻居，就可以实现接近 O (log N) 级别的检索速度！

同样地，我们发现，针对最大内积检索而言，并不是所有边都能贡献效率。我们也成功找到了一种稀疏、高效的选边算法来服务于内积检索。在介绍这个选边策略之前，我们先介绍一下在内积度量下，我们发现一种特殊的几何结构：dominator 和它的 “统治领域”（dominating region）。

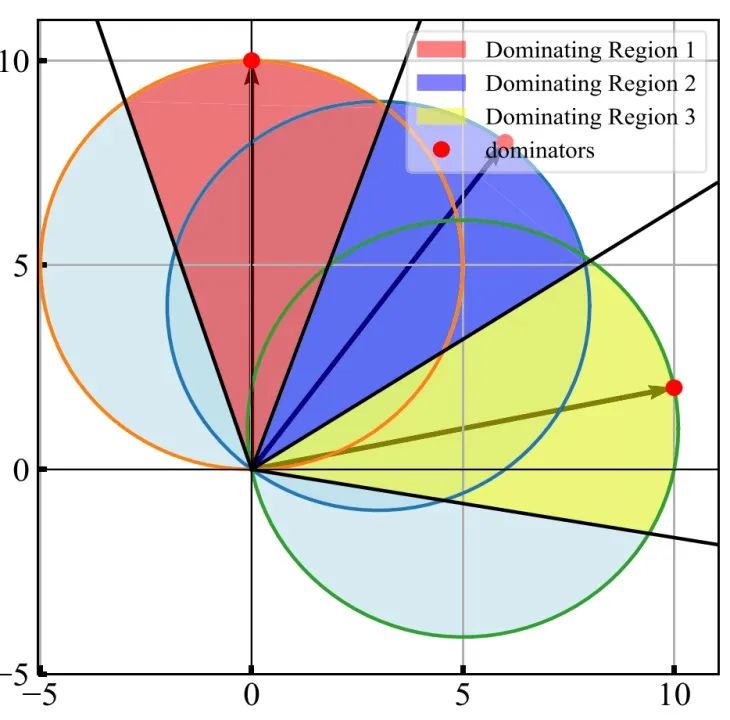
以上图为例，在任意分布的向量集合 D 中，存在这样的一些点 p（图中的三个红点），它们有一片自己的 “统治区域”。在统治区域中的任意向量 q（q 可以不属于 D），能够使得内积 < p,q > 最大化的点，只有 p 自己。换句话说，这些 q 的最大内积邻居，就只有 “统治” 它们的这个唯一的 p。那么，这些 p 就被命名为 dominator，而它们自己对应的统治区就被叫做 p 的 dominating region。比如图中三个红点对应了红黄蓝三个锥状的统治区。我们证明，在一个有限的向量集合 D 上，dominator 集合 P 是 D 的一个子集，P 所决定的所有 “圆锥形” 统治区，构成了 D 所在向量空间的一个有限切分。

了解这个 dominator 的概念有什么意义呢？试想，如果我们能够以低成本的方式标记出一个数据集的所有 dominator，那么，我们就已经拿到内积检索的 “参考答案” 了！这是因为对于任意一个 query 向量 q，只要能知道它落在哪个 dominator 的统治区，就能立刻得到内积检索的解！

于是，我们设计了如下的低成本的 dominator 筛选方案，并将它们都和图中与之最近的点连上边，于是就会得到一个 “条条大路通罗马” 的 dominator 图，命名为 NDG（Naive Dominator Graph）。

当然，类似 NSG 的写作思路，NDG 其实是一个理想最优的图索引，其 O (N^2 log N) 的构建复杂度是难以实用的。为此我们也提出了一种近似方案，在 O (N log K) 的时间内完成索引构建（K << N）。

有 dominator 也就一定有非 dominator，这里我们也给出了一个简单的图例来展示 dominator 王国里，不同点的不同角色关系：

神奇的是，我们发现，有的 dominator “驻扎” 在自己的统治区（self-dominator），有的则呆在别人的统治区，没有统治区的，就是 “平民”—— 非 dominator 了。我们通过统计分析的方式，给出了一个数据集中 self-dominator 比例的估计方式：

04 异构图的构建和检索

到这里，我们已经对齐了欧式度量和内积度量的颗粒度了：

1）欧式选边策略（NSG）和内积选边策略（NDG），保证了两类度量下的图的稀疏性，利于高效存储。

2）O (N log K) 的构建索引速度，保证两类边的筛选过程可在上亿级别数据上高效扩展。

I have an NSG, I have an NDG, Boom! MAG (Metric Amphibious Graph)!

没错！接下来的内容就非常直给，MAG 的本质，就是两大度量空间下优势算法的有机结合。

1）在欧式空间，我们选择 NSG 作为基础结构的原因在于它速度快于 HNSW，且内存占用比 HNSW 少 50% 以上。

2）在内积空间，我们构建 NDG 作为 MAG 图最终边集合的候选池，补足 NSG 在内积检索下非最优的问题。

我们通过大量的实验，发现了以下的现象：

1）NSG 选出来的 “欧式边” 更关注 “邻域”，缺少长距离的连接能；NDG 选出来的 “dominator 边” 关注大跨度的、从任意点到 dominator 的连接，往往是长距离连接。两者形成互补。

2）不同 AI 模型产出的向量数据分布大相径庭。通过调节图结构中 “欧式边” 和 “内积边” 的比例，可以找到最优性能配置。

3）在不同数据分布上，用不同度量进行配合检索也有意想不到的效果！

①一般情况下，先进性欧式最小距离搜索，再进行最大内积搜索是最优顺序。

②适合内积检索的数据，先进行较少步最小欧式搜索，再进行最大内积搜索到最后，可以达到更好性能。

③适合欧式检索的数据，进行比较多的欧式搜索，最后记不切换最大内积或者不切换，可以提升性能。

05 MAG 使用指南

通过前文的观察，我们可以理解 MAG 的真正用法：当不确定应该用什么度量的时候，可以用以下的探测方式：

1）构建好充足的 NSG 和 NDG 的边作为候选，存在 disk 上。

2）收集一批 query 作为探测集。

3）选择一个 (欧式边：内积边) 的比例，确定一个最大总边数，逐渐改变边的比例，把对应的边加载到内存，进行参数扫描。

4）选择一个 (欧式步数：内积步数）的比例，确定一个最大总迭代搜索步数，逐渐改变步数的比例，进行参数扫描。

5）观测到性能先上升后下降，可以记录下最优的参数配置。

因为构建索引是最复杂的，上述步骤省略了重复构建索引的过程，只是在小规模的 query 集合上进行参数搜索，速度是很快的，比如在 10000 个 query 上，针对 1 千万的 base 进行检索，一次可能只需要几秒。进行细粒度的参数扫描，一般也就只需要几分钟就可以完成。

有的读者可能会问，那有没有一眼就可以看出来这个数据更适合哪种趋向的检索呢？当然也有办法，我们通过大量实验给各位用户老爷找到两个简单的统计度量指标。

一个是模长变异系数（Coefficient of Variation Over Norm）。我们先采样计算一定数量的 base 向量的 norm，然后计算 norm 的变异系数 CV = std (norm) /mean (norm)，也就是模长的方差除以均值。CV 高的数据适合偏向内积的搜索，可以从高比例内积边作为起始进行参数调优或者直接选择参数。反之 CV 低的数据适合欧式。

另一个则是聚类指数 DBI（Davies-Bouldin Index）。DBI 定义如下：