线性回归算法

本文内容资源来自 Andrew Ng 在 Coursera上的 Machine Learning 课程，在此向 Andrew Ng 致敬。

摘要
本报告是在coursera学习斯坦福大学机器学习第一二周课程的总结与认识。主要讲述了回归问题，回归属于有监督学习中的一种方法。该方法的核心思想是从连续型统计数据中得到数学模型，然后将该数学模型用于预测或者分类。该方法处理的数据可以是多维的。
下面会介绍单变量线性回归和多变量线性回归。

单变量线性回归（linear regression with one variable）

---

某个目标量可能由一个或多个变量决定，单变量线性回归就是我们仅考虑一个变量与目标量的关系。例如，我们可以仅考虑房子的面积X与房价y的关系，如下图。

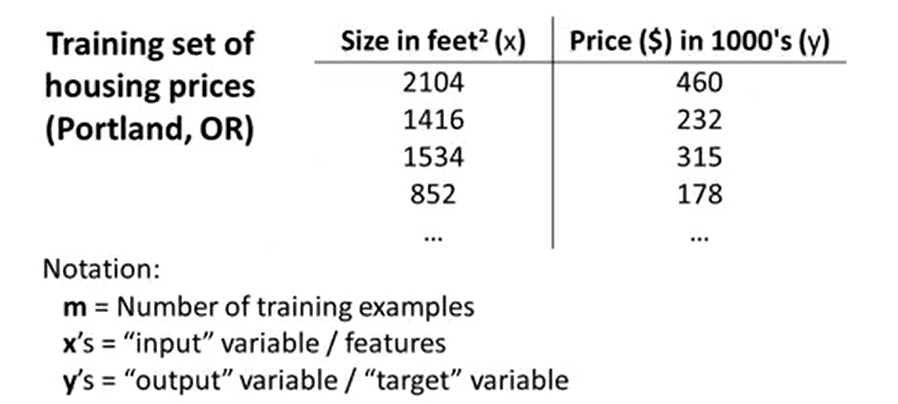
通常将已有的可利用的数据成为dataSet or trainingSet。
我们将用来描述这个回归问题的标记如下：

• m 代表训练集中实例的数量

• x 代表特征/输入变量

• y 代表目标变量/输出变量

• h 代表学习算法的解决方案或函数，也称为假设(hypothesis)

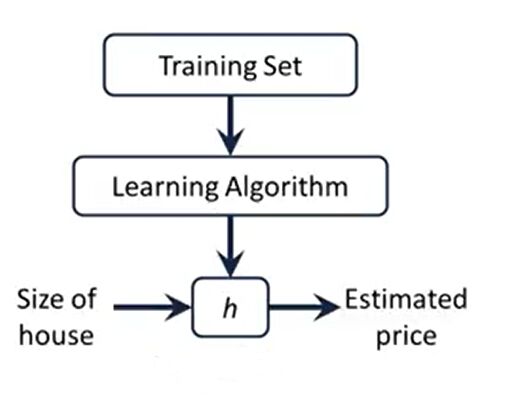
那么，对于房价h，如何表达h？
一种可能的表达方式：hθ(x)=θ0+θ1x ，其中θ0 和θ1为模型参数。
选用此表达方式是由于易入手，这里假设房价与房屋面积呈线性关系。
由于只有一个特征，这样的问题被称为单变量线性回归问题

代价函数（cost function）

---

我们有了假设函数，接下来要做的就是如何选择不同的参数θ0 和θ1。如何来使它来更好的拟合数据呢？我们的想法是hθ(x) 应该最接近 y 值，即问题转化成了一个mininize(hθ(x) -y) 的问题，因此引入一个代价函数Cost Function，也被称作平方误差函数。函数定义如下，每个训练样本 hθ(x)-y 的平方和，再求平均。再乘1/2是为了接下来的计算上的方便。

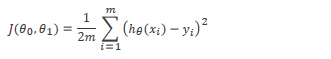
我们想要做的就是关于θ0 和θ1对函数J(θ0 ，θ1)求最小值。即找到使得J(θ0 ，θ1)最小值的时候，θ0 和θ1的值。

梯度下降

---

了解梯度下降前，我们了解一下J(θ0 ，θ1) 的函数图像。
当θ0 为0时，随着的变化θ1 将会得到下图的效果。θ1取1的时候 J 为最小值 。

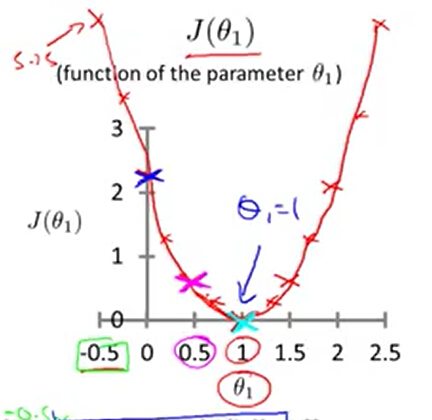
当θ0 和θ1都有值时。

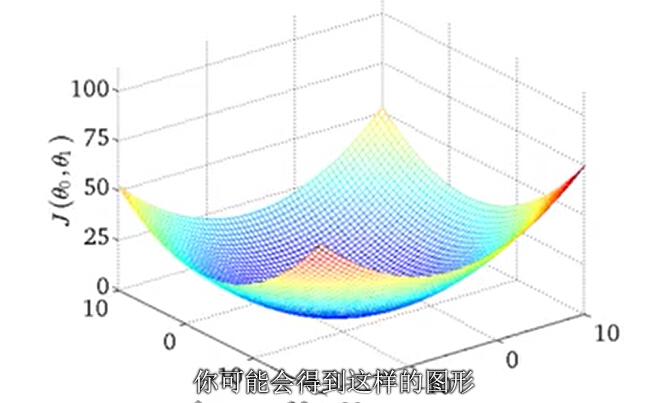
好了，回到我们之前问题描述，我们有一个代价函数J(θ0 ，θ1)，想通过一个算法来使用得 J 最小化。
那么梯度下降的思想就是：
开始给定一个（θ0 ，θ1）初始值，我们想通过不断的改变θ0 ，θ1的值，每次改都使得 J 减少。最终J 减少到最小。

下面通过图来看看梯度下降是如何工作的。
首先想象一下，对θ0 ，θ1赋以某个初始值（一般可以初始化为0）。假设初始化后，J 对应是下图的标红的这个点。
我们想象这是一座山，你站在山上的这个点上。在梯度下降中，我们要做的是看看周围，并问自己我想要通过小碎步下山，朝哪个方向能最快下山？并朝着这个方向前行。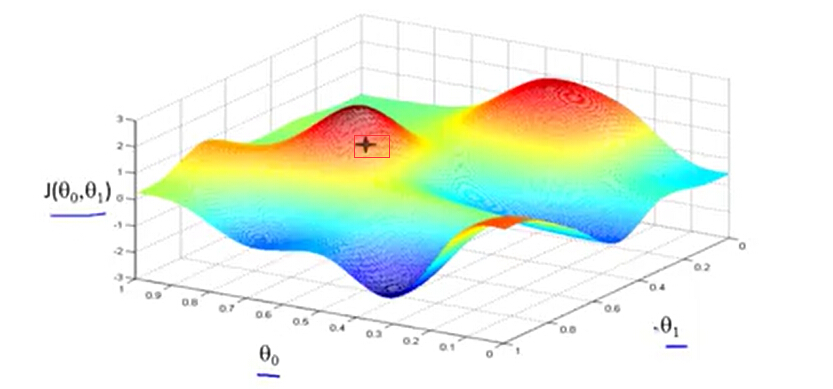
每走一步都需要调整最快的那个方向。最终你走出了这么一条轨迹。最终走到一个局部最优解——山脚下。当然如果你是站在另一个点，你可以会走出另一条轨迹。


上面是通过图直观的感受，那么事实上在这走一步的方向，其实就是梯度的负方向。梯度其实就是J的导数，对于一个线性函数，也就是线的斜率。

如果把每一步的长度定义为学习速率。那么每走一步的这个动作，其实就是 θ0 ，θ1 都朝梯度的负方向进行更新。控制着更新的幅度。

实际上，在线性回归中，代价函数J都是凸函数，可以找到全局最优解

下图是数学定义：即按照一定的学习速率，不断重复更新θ0 ，θ1 直到 J 局部收敛到最小值

其实这个算法被称为批量梯度下降算法（batch gradient descent）：即在每一次更新theta值的时候，都是用了所有的训练样本
其中α是学习率，它决定着沿着能让代价函数下降程度最大的方向向下迈的步子有多大。如果速率太小，则下降的速度比较慢。如果速率过大，会无法收敛到最小值。
α太小，下降速度太慢
α太大，不能收敛，甚至发散
所以如果陷入局部极小，则梯度为0，不会向左右变换，如下：

补充一点，即使alpha值固定了，在梯度下降的过程中步长也会自动逐渐减小，所以我们不需要在函数逼近最小值的时候减小alpha的取值，以防止步长过大可能会跳过最低点。

对线性回归运用梯度下降法

---

关键在于求出代价函数 J 的导数：

则算法改写成：

多变量线性回归（linear regression with multiple variables）

---

（一）多维特征（multiple features）
目前为止，我们探讨了单变量/特征的回归模型，现在我们对房价增加更多的特征，例如房间数楼层等，构成一个含有多个变量的模型，模型中的特征为（x1,x2,x3,…..,xn）

定义：

n = 特征数目

x(i)= 第i个训练样本的所有输入特征，可以认为是一组特征向量

x(i)j = 第i个训练样本第j个特征的值，可以认为是特征向量中的第j个值

对于Hypothesis，不再是单个变量线性回归时的公式：hθ(x)=θ0+θ1x
而是：

$$h_\theta(x)=θ_0+θ_1x_1+θ_2x_2+…+θ_nx_n$$

为了方便，记x0 = 1，则多变量线性回归可以记为：

$$h_θ(x)=θ^Tx$$
其中θ和x都是向量。T表示矩阵转置。

（二）多变量梯度下降（gradient descent for multiple variable）
与单变量线性回归类似，在多变量线性回归中，我们也构建一个代价函数，则这个代价函数是所有建模误差的平方和，即：

$$J(\theta) = J(\theta_0, \theta_1, … ,\theta_n) = \frac{1}{2m}\sum_{i=1}^m{(h_\theta(x^{(i)}) – y^{(i)})^2}$$
我们的目标和单变量线性回归问题中一样，是要找出使代价函数最小的一系列参数：
梯度学习算法如下：

左边为单变量学习方法，右边为多变量学习方法。

（三）特征缩放

1.

下面我们来介绍一些关于梯度下降运算中的实用技巧，首先是特征缩放 (feature scaling) 方法。

如果你有一个机器学习问题，并且这个问题有多个特征。如果你能确保这些特征都处在一个相近的范围（确保不同特征的取值在相近的范围内），这样梯度下降法就能更快地收敛。

具体来说，假如你有一个具有两个特征的问题，其中 x1 是房屋面积大小，它的取值在0到2000之间，x2 是卧室的数量，这个值取值范围在1到5之间。如果你画出代价函数J(θ) 的轮廓图：

那么这个轮廓看起来，应该是如上图左边的样子。

J(θ) 是一个关于参数 θ0 、θ1 和 θ2 的函数，我在此处忽略 θ0 （暂时不考虑 θ0）。并假想一个函数的参数，只有 θ1 和 θ2，但如果变量 x1 的取值范围远远大于 x2 的取值范围的话，那么最终画出来的代价函数 J(θ) 的轮廓图就会呈现出这样一种非常偏斜并且椭圆的形状。2000和5的比例会让这个椭圆更加瘦长。

所以，这是一个又瘦又高的椭圆形轮廓图，正是这些非常高大细长的椭圆形构成了代价函数 J(θ)，如果你用这个代价函数来进行梯度下降的话，你要得到梯度值最终可能需要花很长一段时间才能得到。并且可能会来回波动，然后会经过很长时间，最终才收敛到全局最小值。

事实上，你可以想像如果这些轮廓再被放大一些的话，如上图最左边的那样（如果你画的再夸张一些，把它画的更细更长），那么可能情况会更糟糕。梯度下降的过程可能更加缓慢，需要花更长的时间，反复来回振荡，最终才找到一条正确通往全局最小值的路。
在这样的情况下一种有效的方法是进行特征缩放(feature scaling)。

2.

举例来说，把特征 x 定义为房子的面积大小除以2000，并且把 x2 定义为卧室的数量除以5。如此一来，表示代价函数 J(θ)的轮廓图的形状偏移就会没那么严重，也许看起来会更圆一些。

如果你用这样的代价函数，来进行梯度下降的话，那么梯度下降算法就会找到一条更快捷的路径通向全局最小，而不是像刚才那样，沿着一条让人摸不着头脑的路径、一条复杂得多的轨迹来找到全局最小值。

因此，通过特征缩放，通过“消耗掉”这些值的范围（在这个例子中，我们最终得到的两个特征 x1 和 x2 都在 0 和 1 之间），你得到的梯度下降算法就会更快地收敛。

更一般地，我们执行特征缩放，将特征的取值约束到-1 到 +1 的范围内（注意：特征 x0 是总是等于1，已经在这个范围内）。但对其他的特征，我们可能需要通过除以不同的数来让它们处于同一范围内。-1 和 +1 这两个数字并不是太重要。

所以，你所认可的范围可以大于或者小于 -1 到 +1 的范围，但是也别太大或者太小到不可以接受的范围。通常不同的人有不同的经验，但是我们一般是这么考虑的：如果一个特征是在 -3 到 +3 的范围内，那么你应该认为这个范围是可以接受的。但如果这个范围大于了 -3 到 +3 的范围，我们可能就要开始注意了。如果它的取值在 -1/3 到 +1/3 的话，我们觉得也还不错，可以接受，或者是 0 到 1/3 或 -1/3 到 0 这些典型的范围，我们都认为是可以接受的。但如果特征的范围取得很小的话，你就要开始考虑进行特征缩放了。

总的来说，不用过于担心你的特征是否在完全相同的范围或区间内，只要他们足够接近的话，梯度下降法就会正常地工作。

3.

除了在特征缩放中，将特征除以最大值以外，有时我们也会进行一个称为均值归一化的工作(mean normalization)
规律是，你可以用如下的公式：

$$x_i \leftarrow \frac{x_i – \mu_i} {S_i}$$
来替换相对较大/小的特征。
其中，Si可以是特征的取值范围（最大值-最小值），也可以是标准差(standard deviation)。

（四）学习率（learning rate）
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

具体地说，如果代价函数 J(θ) 随迭代步数的变化曲线是上图左上角的这个样子，J(θ) 实际上在不断上升，那么这就很明确的表示梯度下降算法没有正常工作。

而这样的曲线图，通常意味着你应该使用较小的学习率 α。

同样的 有时你可能看到上图左下角这种形状的 J(θ) 曲线，它先下降，然后上升，接着又下降，然后又上升，如此往复。

而解决这种情况的方法，通常同样是选择较小 α 值。

我们并不打算证明这一点，但对于我们讨论的线性回归，可以很容易从数学上证明，只要学习率足够小，那么每次迭代之后，代价函数 J(θ)都会下降，因此如果代价函数没有下降，那么可以认为是学习速率过大造成的。此时，你就应该尝试一个较小的学习率。
当然，你也不希望学习速率太小。因为如果这样，那么梯度下降算法可能收敛得很慢。

总结一下：

如果学习率 α 太小，你会遇到收敛速度慢的问题，而如果学习率 α 太大，代价函数 J(θ) 可能不会在每次迭代都下降，甚至可能不收敛，在某些情况下，如果学习率 α 过大，也可能出现收敛缓慢的问题。但更常见的情况是，你会发现代价函数 J(θ)，并不会在每次迭代之后都下降。

而为了调试所有这些情况，绘制J(θ)随迭代步数变化的曲线，通常可以帮助你弄清楚到底发生了什么。

具体来说，当我们运行梯度下降算法时，通常会尝试一系列α值，如：

…,0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1,…

然后对于这些不同的 α 值，绘制 J(θ)随迭代步数变化的曲线，然后选择看上去使得 J(θ)快速下降的一个 α 值。

所以，在为梯度下降算法选择合适的学习率时，可以大致按3的倍数来取值一系列α值，直到我们找到一个值它不能再小了，同时找到另一个值，它不能再大了。然后我尽量挑选，其中最大的那个 α 值，或者一个比最大值略小一些的合理的值。当我们做了以上工作时，通常就可以得到一个不错的学习 速率值。

多项式回归（polynomial regression）**

---

线性回归并不适合所有数据，有时我们需要曲线来适应我们的数据，比如一个二次方模型

$$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2$$
或者一个三次方模型：$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3$

通常我们需要先观察数据然后再决定准备尝试怎样的模型。
另外，我们可以令：

$x_2=x_2^{2}$

$x_3=x_3^{3}$

从而将模型转化为线性回归模型。注意：如果采用多项式回归模型，在运行梯度下降算法，特征缩放非常有必要。

除了转而建立一个三次模型以外，你也许有其他的选择特征的方法，如下：

正规方程（normal equation）

---

之前，我们一直都在使用梯度下降算法，但是对于某些线性回归问题，正规方程式更好的解决方案。

正规方程通过求解以下的方程：

假设我们的训练特征矩阵为X（包含了X0=1）并且我们的训练集结果为向量 y ，则利用正规方程解出向量 :

$$\theta=(X^T \times X)^{-1}\times X^T\times y$$
标注：T表示矩阵X的转置，-1 表示矩阵X的逆

我们使用房价预测问题的数据：

数据包括四个特征（不包括X0），我们加入X0=1，这时候我们使用正规方程方法来求解：

在Matlab/Octave中，正规方程写作：pinv(X’ * X)*X’*y

这里有一个需要注意的地方，有些不可逆的矩阵（通常是因为特征之间并不独立，比如同时包含英尺为单位的尺寸和米为单位的尺寸这两个特征，也有可能是特征数量大于训练集的数量，比如有2000个特征但是只有1000个训练集），正规方程方法是不能够使用的。
那么我们现在有两个机器学习的算法了，一个是梯度下降，一个是正规方程，两个方法比较如下：

在最后，有一点需要注意，并不是所有的X’ * X都可求，存在其不可逆的i情况。这被称作标准化等式不可逆性。此时我们只能进行特征删除，剔除掉一些冗余的特征，再求解。

---

以上就是针对多变量的线性回归，可以看出思想和单变量的差不多，唯一不同的就是要多计算几个值。为了方面，在这里引入了向量的表现形式，同时在计算的时候也应该采用矢量化计算加快计算速度。