机器学习：训练与测试

训练与测试

通过机器学习的可行性分析，我们得到了一些东西。首先根据NFL定理，机器学习可能行不通，随后根据统计学的相关知识，机器学习似乎又是可行的。但是这个似乎的可行性又有一点限制：M必须是有限的。M代表的含义是hypothesis的个数。那么当M是无限的时候机器学习还能进行下去吗？接下来的几篇笔记会对这个问题进行分析。

1.回顾

首先来看基于统计学得到的机器学习的流程图，

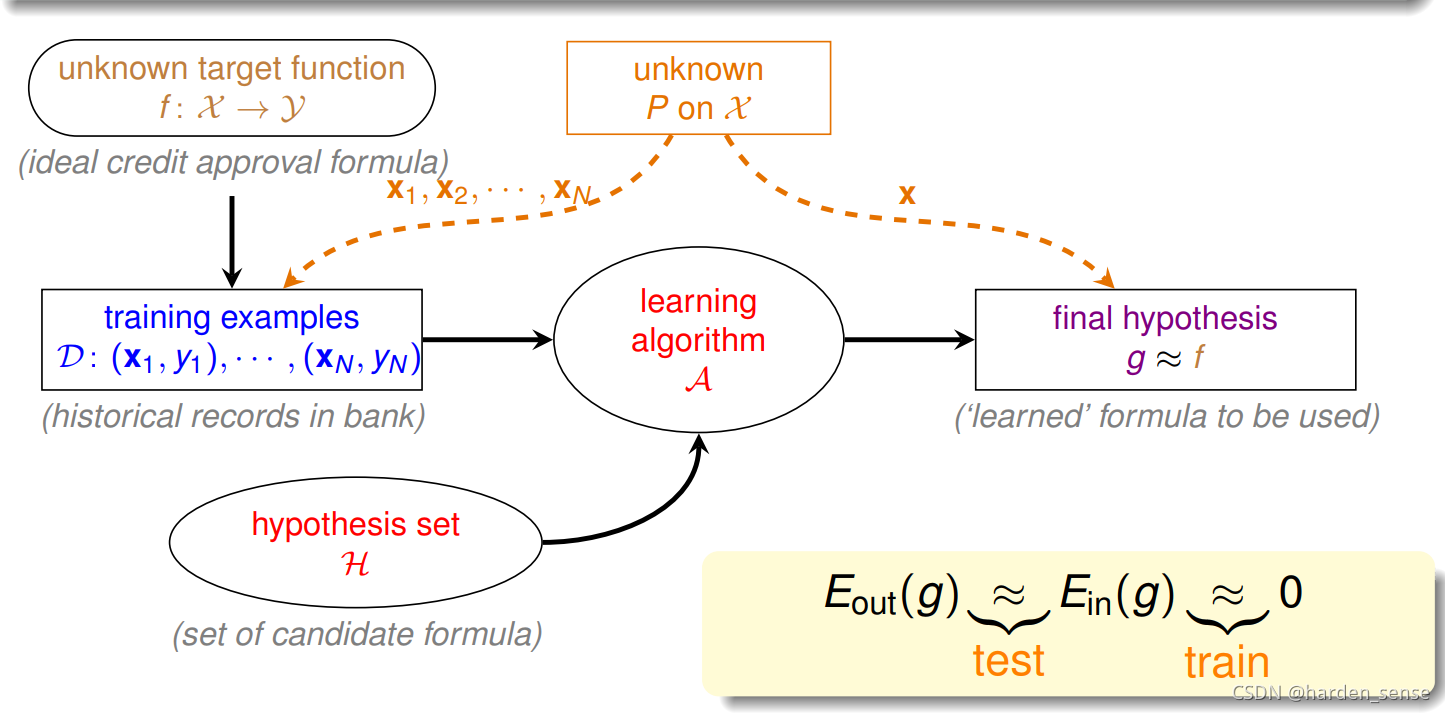
该图中的训练样本D和测试样本都来自同一分布的数据集，这是机器能够学习的前提。训练样本D应该足够的大，M应该是有限的。只有这样根据霍夫定不等式，才能保证出现BAD sample的概率足够的小，演算法可以在M中自由的选择g。保证选出的g $\approx f$。也就是$E_{in}(h)\approx 0$，并且$E_{in}(h)\approx E_{out}(h)$。

总之机器学习的两个核心问题是：

• $E_{in}(h)\approx 0$或者说就是$E_{in}(h)$要足够的小
• $E_{in}(h)\approx E_{out}(h)$。

通过机器学习的可行性分析我们得出，当M是有限的时候，机器学习才能进行下去，那么M和上面两个问题有什么联系呢？

• 假如M是一个比较小的数值。我们可以很容易的满足第二个核心问题，也就是出现的BAD sample的概率很小，我们可以自由的选则g。确保$E_{in}(h)\approx E_{out}(h)$。但是，由于M很小我们能选择的东西并不多，可能会使$E_{in}(h)$的值过大，不能满足第一个要求。
• 那么我们假使M足够的大，能够选择的东西比较多。很容易满足第一个要求，我们可以把$E_{in}(h)$做的足够的小。但是随着M的增大BAD sample出现的概率就会增大，第二个问题就不能满足。

由此看来M的值既不能过大，也不能过小，如果M无限大，那么是不是就意味着，机器不能进行学习了呢？列如PLA中，可供选择的直线有无数条，但是PLA仍然可以进行学习。这又是什么原因呢？如果我们能将无限大的M限定在一个范围内，问题似乎就解决了。

2.把线分类

根据霍夫定不等式：$$P[\mid E_{in}(h)-E_{out}(h)\mid >ϵ]\le 2Mexp(-2{ϵ}^{2}N)$$
其中M表示hypotheses中可供选择函数的个数。每个hypothesis下的BAD events $B_m$级联的形式满足下列不等式：

当M无限大时，右边的不等式值将会很大，也就是说BAD events很大，$E_{in}(g)$与$E_{out}(g)$不会非常的接近。但是BAD events $B_m$实际上扩大了上界。这种假设的做法，忽略了各个hypothesis之间的交集。这是最坏的情况，实际上他们之间会有交集如下图所示，真实的M并没有那么大。

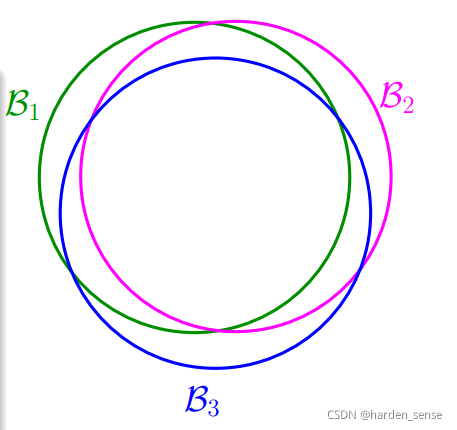
也就是说union bound被估计过高了（over­estimating）。所以，我们的目的是找出不同BAD events之间的重叠部分，也就是将无数个hypothesis分成有限个类别。那么该如何对M进行分类呢？我们看下面的一些列子：

在平面上将点用直线分开，就像PLA做的事情一样。首先假如平面上只有一个点，我们的分法只有两种。要么将这个点分为+1，要么就是-1

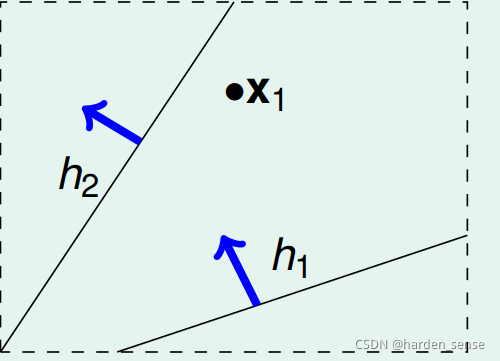
虽然M有无限多，但是在这个列子中，真实有效的M只有两类，我们记为$M_h$。

如果平面上有两个点$x_1,x_2$，那么可能的分法有四种

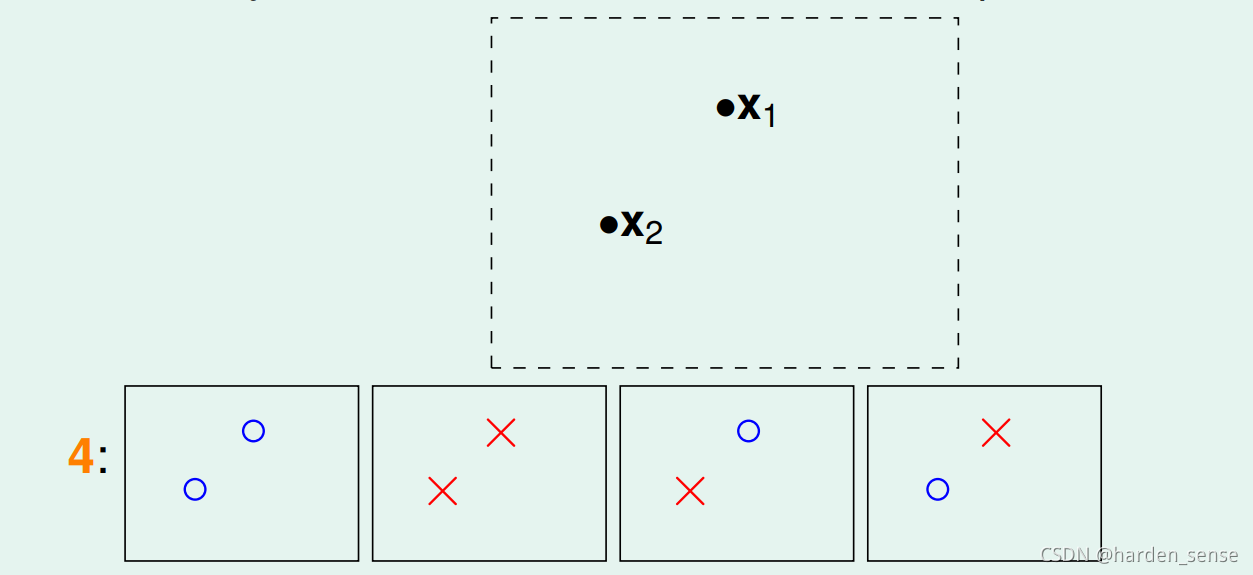
同样的道理三个点共有八种分法：

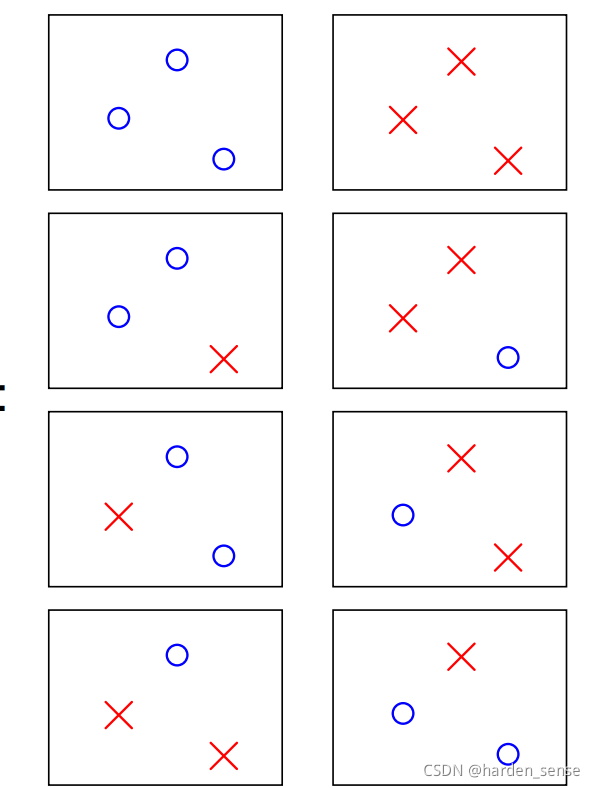
但是三个点的时候，有一些情况是不能用直线进行划分的：

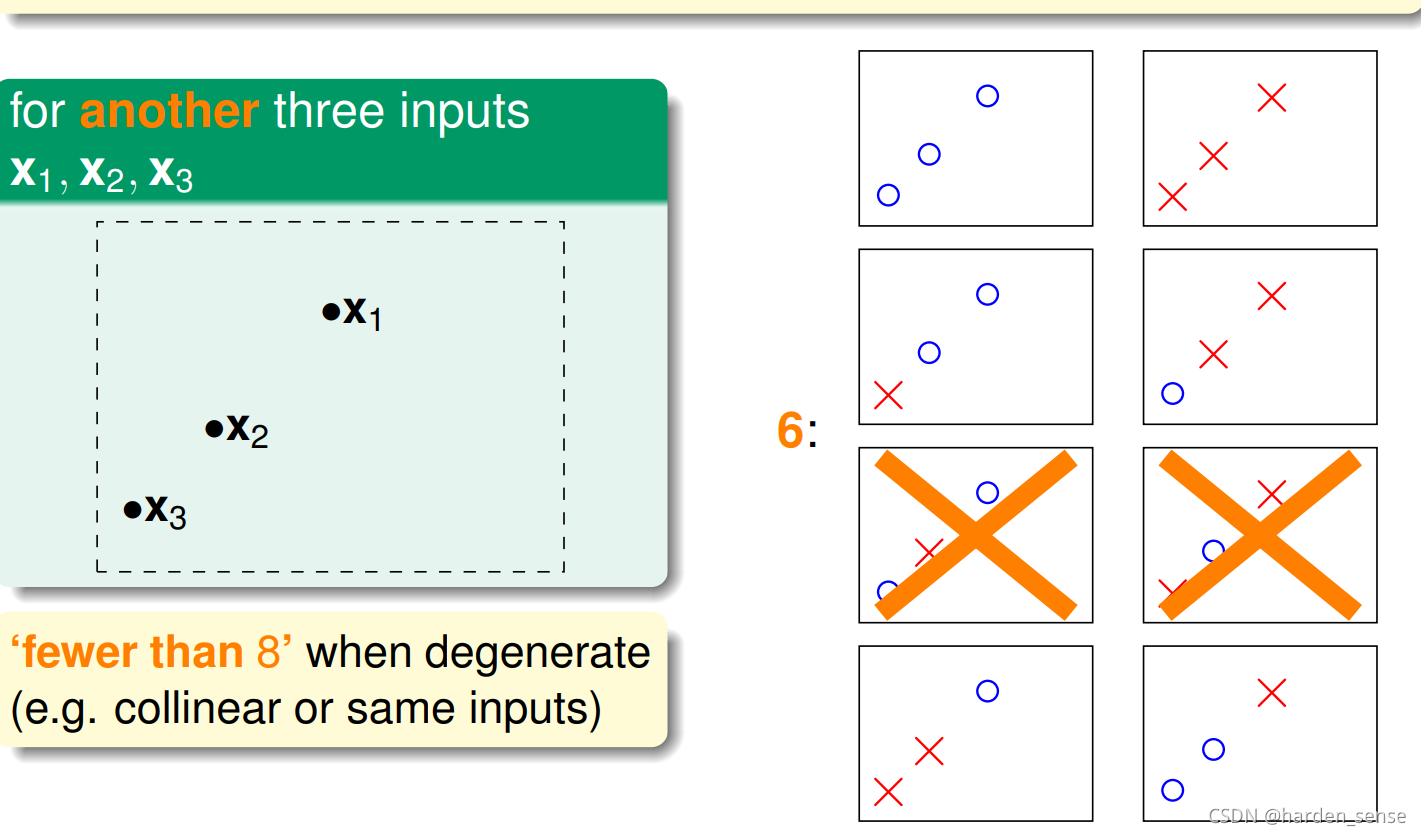
接着往下看，四个点时的情况：

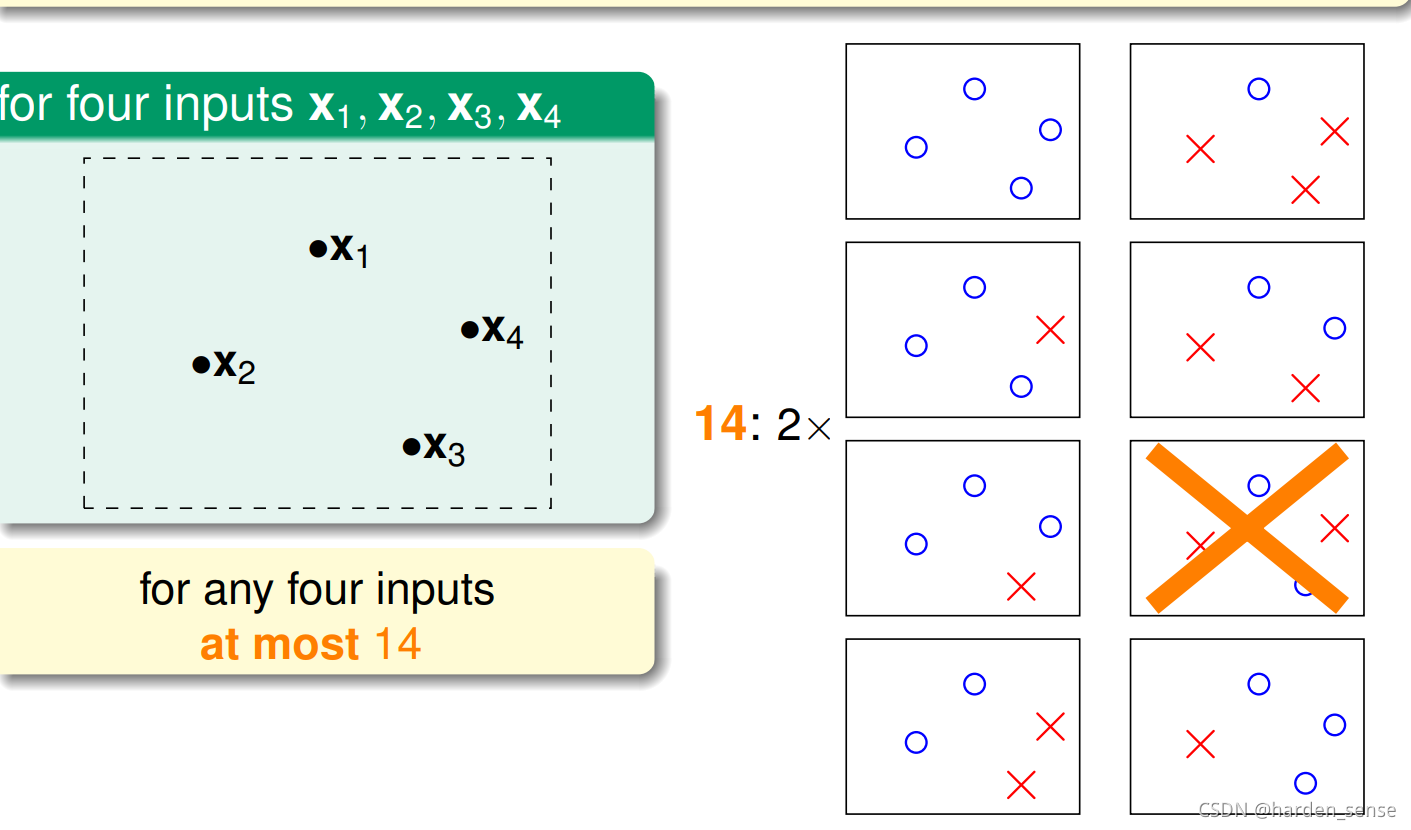
不管输入空间是什么样子的。总会有两种情况，无法用直线进行划分。也就是说找不到一条直线，能将四个点组成的16种情况全部分开。

通过上面的分析我们得出，平面上线的种类是有限的。1点最多两种线，2个点最多四种线。3个点最多八种线，4个点最多14种线（<$2^4$）。不管怎么说平面上线的种类<<$2^N$,其中N为样本点的个数。所以我们可以对霍夫定不等式进行一个改写：$$P[\mid E_{in}(h)-E_{out}(h)\mid >ϵ]\le 2\ast effect(N)exp(-2{ϵ}^{2}N)$$
effect(N)：N个样本点中，直线的种类。

在这种情况下，即使M是无限的，effect（N）<$2^N$，不等式的右边也会趋近于0，机器学习就是可能的。

3.Hypotheses中有效线的种类

接下来先介绍一个新名词：二分类（dichotomy）。dichotomy就是将空间中的点（例如二维平面）用一条直线分成正类（蓝色o）和负类（红色x）。令H是将平面上的点用直线分开的所有hypothesis h的集合，dichotomy H与hypotheses H的关系是：hypotheses H是平面上所有直线的集合，个数可能是无限个，而dichotomy H是平面上能将点完全用直线分开的直线种类，它的上界是 。接下来，我们要做的就是尝试dichotomy代替M。

接下来在看一个新的名词，**成长函数（growth function）**记为$M_H(H)$。成长函数的定义是：对于由N个点组成的不同集合中，某集合对应的dichotomy最大，那么这个dichotomy值就是$M_H(H)$。他的上界为 $2^N$

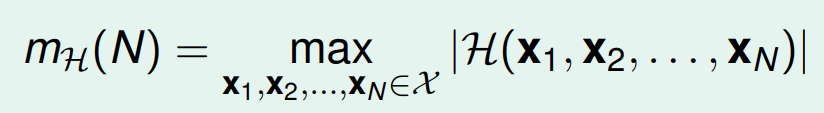
成长函数也就是我们前面所说的线的种类，在二维平面上我们有这样一个关系：

接下来的问题就是如何去计算成长函数。先看一种简单的情况一维的Positive Rays：

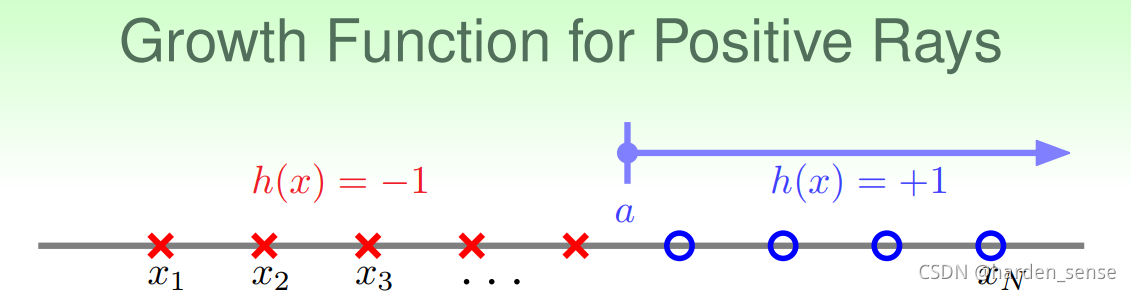
N个点，只能用一个方向的直线进行分割，最大分割方法是N+1。也就是说$M_H(H)=N+1$<<$2^N$,这个结果正是我们需要的。

在看另一种情况，一维的Positive Intervals：

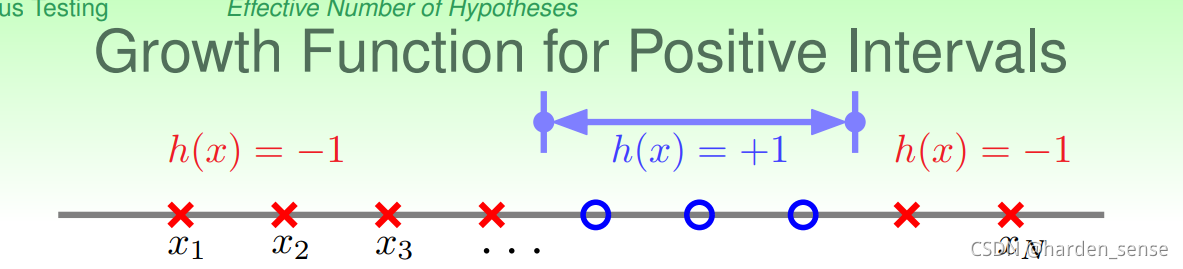
我们可以任选一条线段，将样本分为不同的两个部分，总共可能的结果为：$\frac{1}{2}{N}^2+\frac{1}{2}N+1$,也即$M_H(H)=$$\frac{1}{2}{N}^2+\frac{1}{2}N+1$<<$2^N$,这个结果也是我们希望看到的。

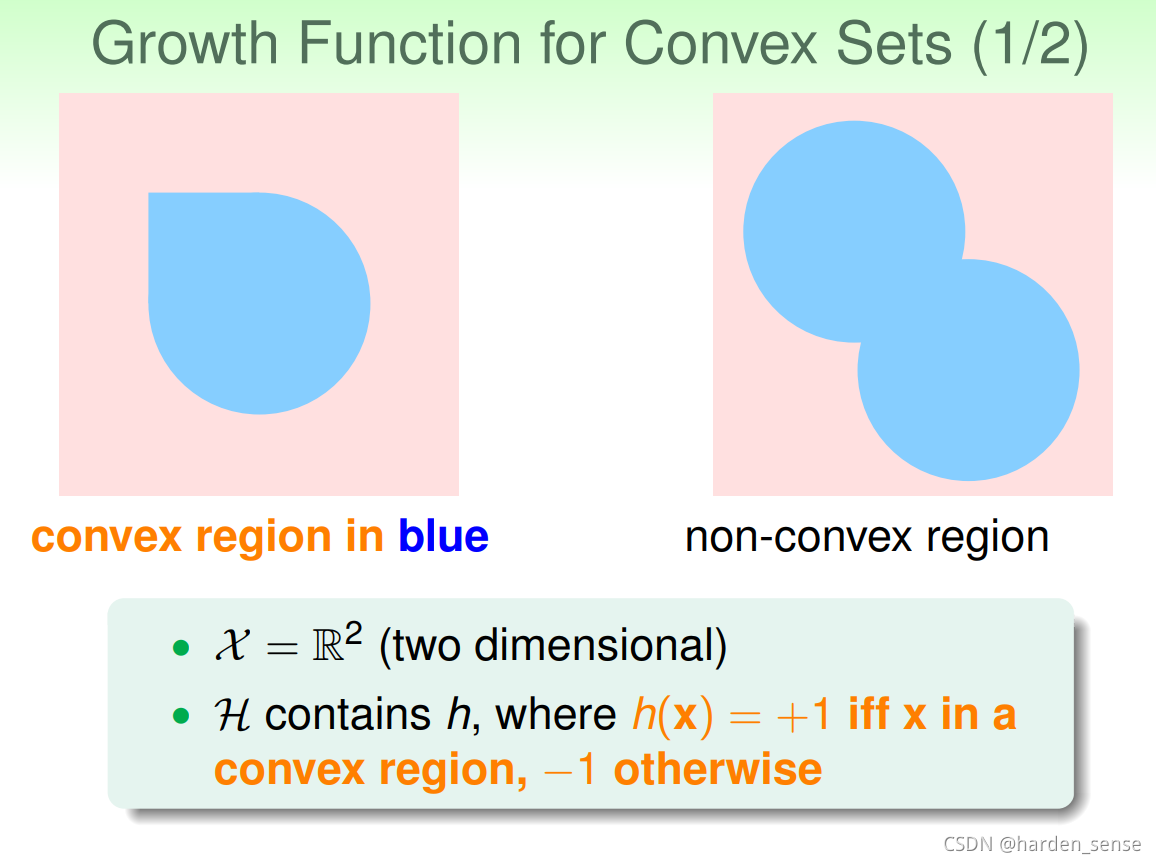
再来看个列子，假设在二维空间里，如果hypothesis对应得是凸多边形构成的曲线，或者类圆得图形。那么他的成长函数是多少呢？我们不做推导，他的结果是$2^N$

4.Break Point

我们截止目前为止了解了四种成长函数：

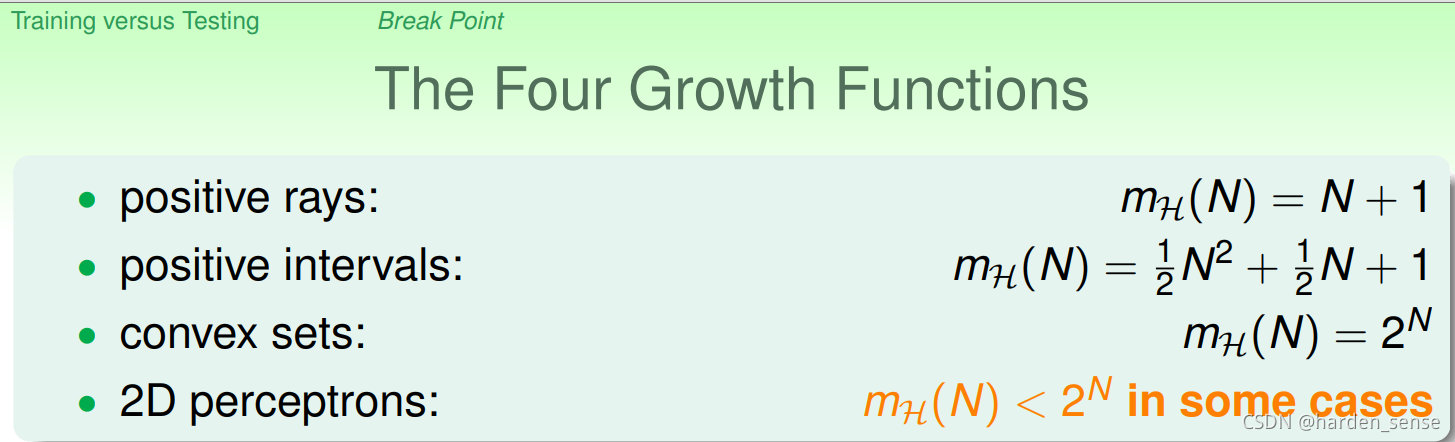
我们介绍成长函数的目的就是希望用成长函数代替霍夫定不等式中的M，如果成长函数是polynomial（多项式），那么完全可以用成长函数来代替M，而对于convex sets他的成长函数的增长是无限的，并不能保证机器学习的可能性。那么，对于2D perceptrons，它的成长函数究竟是polynomial的还是exponential的呢？

对于2D perceptrons我们分析了四个点，前三个点都是满足$2^N$的增长，一直到第四个点，就无法在做出16个分类了。我们把这第四个点称为2D perceptrons
的break point（5，6，7，8等等）都是break point。有k个点，如果k大于break point时，它的成长函数一定小于2的k次方。

根据break point的定义，当$M_M(H)\ne$ $2^k$时，最小的就是break point。我们来看之前得到的四种成长函数。

通过观察我们可以发现，成长函数和break point之间有某种关系。对于convex sets，没有break point，它的成长函数是2的N次方；对于positive rays，break point k=2，它的成长函数是O(N)；对于positive intervals，break point k=3，它的成长函数是$O(N^2)$。基于这种发现，我们可以推论2D perception$M_H(H)=O(2^{K-1})$,如果成立的话，我们就可以用$M_H(H)$来代替M，机器就能够学到一些东西了。

5.结论

只要存在break point，那么其成长函数就满足多项式的增长，推导过程比较麻烦，不详细看了。总之机器学习是可能的。