彻底计数排序和基数排序

随机化快速排序、堆排序、归并排序、插入排序都是比较模型的排序，最好的情况下时间复杂度是O(nlgn)，那有没有比nlgn更快的呢？答案是有的，利用空间换时间，那就是计数排序和基数排序。

计数排序

参考：计数排序
Java实现：

import java.util.Arrays;

public class CountingSort {
    public static void main(String[] args) {
        int[] a = {4, 1, 3, 4, 3};
        int max = 0;
        for (int i = 0; i < a.length; i++) {
            if (max < a[i]) {
                max = a[i];
            }
        }
        System.out.println(max);
        int[] result = new int[a.length];
        countSorting(a, result, max);
        System.out.println(Arrays.toString(result));
    }

    private static void countSorting(int[] a, int[] result, int max) {
        int[] position = new int[max + 1];
        int n = a.length;

        // 统计数组a中每个元素的个数, position数组的下标其实就是a数组对应元素的值, 类似一个hash表
        // 是0就表示这个元素不存在
        for (int i = 0; i < n; i++) {
            position[a[i]]++;
        }

        // 将position数组的前一项和后一项相加
        // position的下标是i, position[i]就表示在数组a中, 小于等于i的元素个数
        // position[i] = n, n就是元素i在 有序result数组中的位置
        for (int i = 1; i < position.length; i++) {
            position[i] = position[i] + position[i - 1];
        }

        // 根据position中保存位置信息, 将a中的元素放入result中, 同时position数组中的值减1
        // 从而result就是一个有序的数组了
        for (int i = n - 1; i >= 0; i--) {
            int sortPos = position[a[i]] - 1;
            result[sortPos] = a[i];
            position[a[i]]--;
        }
    }
}

计数排序图示：

稳定的排序算法会保证相同元素的相对位置，计数排序是稳定的排序算法。

假设position.length = k, 时间复杂度就是几个for循环次数之和，总共是k + 2n，加上初始化position数组的复杂度k就是2(k+n)，忽略常数，时间复杂度就是O(k+n)。当这个k很大时，辅助空间position会占用很多内存，可能会出现使用率不高的情况，所以计数排序的空间复杂度还可以进一步的优化。下边的基数排序在内存空间的使用率上会更有优势。

基数排序

参考:
基数排序与桶排序，计数排序【详解】
排序算法系列：基数排序
这两篇文章写得很好，我只是代码的搬运工。

基数，以10进制为例，就是0-9的数，对每一个数进行拆分就是个位、十位、百位等。看图示：

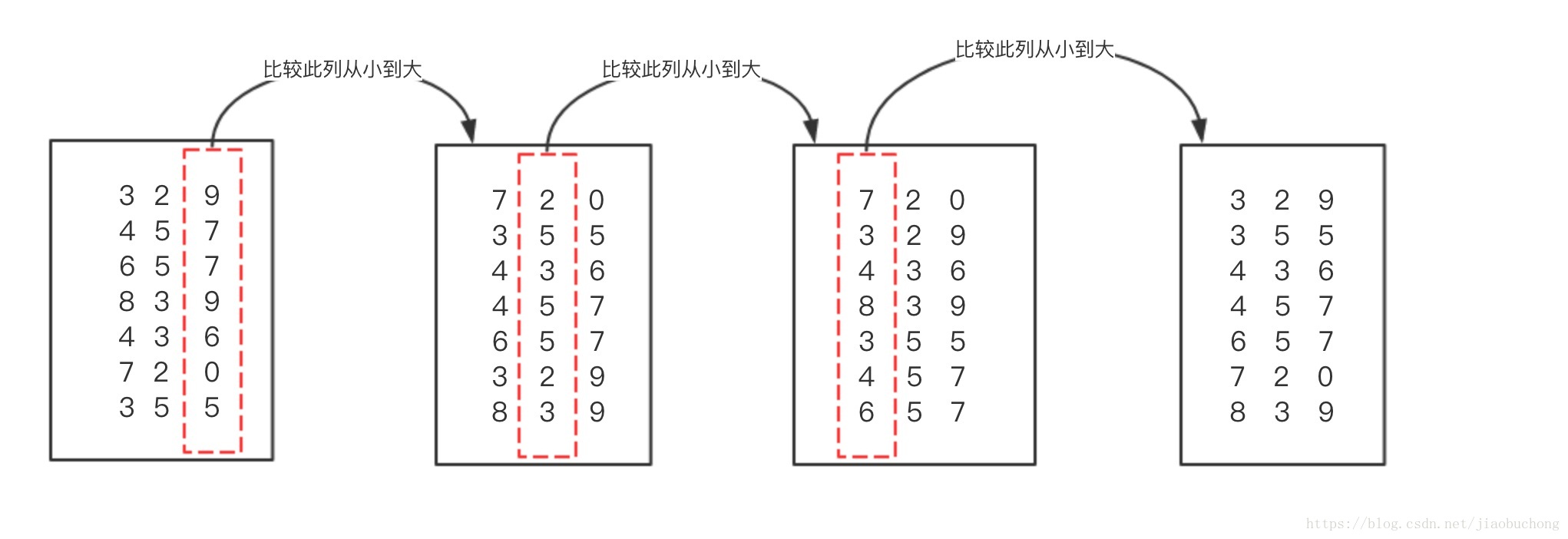
Java代码实现：

import java.util.Arrays;

public class RadixSort {

    public void radixSort(int[] a) {
        if (a == null || a.length < 1) {
            return;
        }
        int maxVal = 0;
        int arraySize = a.length;
        for (int i = 0; i < arraySize; i++) {
            if (a[i] > maxVal) {
                maxVal = a[i];
            }
        }

        int digitPosition = 1;
        // 对应上边 计数排序 时的result数组
        int[] bucket = new int[a.length];

        while (maxVal / digitPosition > 0) {
            // 下面走的计数排序
            int[] position = new int[10];
            for (int i = 0; i < arraySize; i++) {
                position[a[i] / digitPosition % 10]++;
            }
            for (int i = 1; i < position.length; i++) {
                position[i] = position[i] + position[i - 1];
            }
            for (int i = arraySize - 1; i >= 0; i--) {
//                bucket[--position[a[i] / digitPosition % 10]] = a[i];
                int target = a[i] / digitPosition % 10;
                int sortPos = position[target] - 1;
                bucket[sortPos] = a[i];
                position[target]--;
            }

            for (int i = 0; i < arraySize; i++) {
                a[i] = bucket[i];
            }
            digitPosition = digitPosition * 10;
        }
    }

    public static void main(String[] args) {
        int[] a = {329, 457, 657, 839, 436, 720, 355};
        RadixSort radixSort = new RadixSort();
        radixSort.radixSort(a);
        System.out.println(Arrays.toString(a));
    }
}

计数排序的时间复杂度是O(k+n)，如果待排序数组中最大的数字位数为d，那基数排序的时间复杂度就是O(d*(k+n))。

空间申请就是bucket数组和position数组，相比计数排序，空间的节省都在position数组，为固定的长度10，虽然节省了空间，但运行时间比计数排序会多些，要进行多轮次的计数排序。