字符串字典序

字符串字典序

设字母集为$\sum$（通常为小写字母），${\sum }^{\ast }$ 为表示包含所有有限长度的字符串的集合，该字符串是由字母表$\sum$中字符组成的，而字典序是定义在${\sum }^{\ast }$上的一个偏序关系。

设两个字符串为$a$与$b$，则两个字符串的大小关系为：

1. 令$i=1$。
2. 若 i ≤ min ⁡ { ∣ a ∣ , ∣ b ∣ } i \leq \min\{|a|,|b|\} i≤min{∣a∣,∣b∣}比较$a[i]$和$b[i]$之间的关系，若$a[i]<b[i]$，那么$a$的字典序小于$b$，若$a[i]>b[i]$，那么$a$的字典序大于$b$，若$a[i]=b[i]$那么令$i+1$，继续比较。
3. 若 i > min ⁡ { ∣ a ∣ , ∣ b ∣ } i > \min\{|a|,|b|\} i>min{∣a∣,∣b∣}，若$|a|<|b|$，那么$a$的字典序小于$b$，若$|a|>|b|$，那么$a$的字典序大于$b$，若$|a|=|b|$那么两个字符串的字典序相同。

例题

字符串拼接问题

ABC 225F

给定$N$个字符串，从中选取$J$个字符串，拼接顺序自定，求字典序最小的拼接结果字符串。

首先列举$4$个错误的做法：

第一种：

直接对$S_i$按照字典序进行排序，然后取出前$J$个字符串拼接在一起。

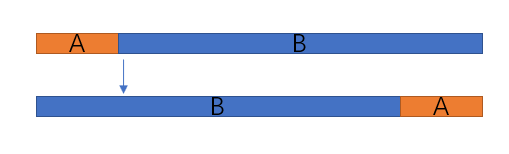
假设，$J=2$，$A$是$B$的一个前缀，并且$|A|<|B|$，这样按照第一种排序得到的下图最上面的字符串，而下面的字符串可能更优，考虑下图箭头处的比较位置，若在箭头处下面的字符串的字典序小于上面的字符串，那么下面的字符串才是最优解，因此第一种不可行。

例如：

2 2
b
ba

第二种：

定义排序规则：若下标$i$和$j$满足$S_i+S_j<S_j+S_i$，那么$S_i$应该排列在$S_j$的前面，那么取出前$J$个拼接即可。

考虑下述样例：

2 1
b
ba

由于第一种的错误性间接导致了第二种错误。

第三种：

定义排序规则：若下标$i$和$j$满足$S_i+S_j<S_j+S_i$，那么$S_i$应该排列在$S_j$的前面，那么取出前$J$个拼接即可。

然后进行DP，设$dp[i][j]$是前$i$个字符串里挑选$j$个字符串的最小字典序结果串，有以下状态转移方程：

$$dp[i][j]=\min (dp[i-1][j],dp[i-1][j-1]+S_i)$$

转移方程中$dp[i-1][j-1]+S_i$，并不一定是最小的以$S_i$结尾的字典序，如图：

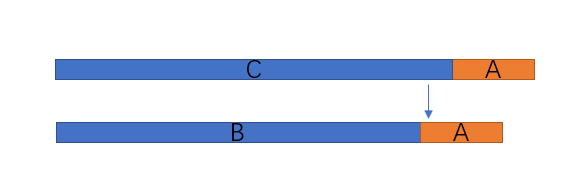
$B$是$C$的一个前缀，如果按照上述DP方程转移，得到的是下面的答案，但是如果考虑箭头比较的位置，那么上面的字符串的更优。

考虑下面的样例：

3 2
baa
ba
b

第四种：

定义排序规则：若下标$i$和$j$满足$S_i+S_j<S_j+S_i$，那么$S_i$应该排列在$S_j$的前面，那么取出前$J$个拼接即可。

然后进行DP，设$dp[i][j]$是前$i$个字符串里挑选$j$个字符串的最小字典序结果串，有以下状态转移方程：

$$dp[i][j]=\min (dp[i-1][j],\underset{k<i}{\min }dp[k][j-1]+S_i)$$

由第三种推广可知，由前$k$个组成的最小字典序拼接$S_i$不一定是最小的字典序，其本质原因出现在字符串前缀的问题上。

正确做法：

定义排序规则：若下标$i$和$j$满足$S_i+S_j<S_j+S_i$，那么$S_i$应该排列在$S_j$的前面，那么取出前$J$个拼接即可。

可以保证，答案就是在排序好的序列中，挑选出$J$个字符串，然后按照相对位置拼接，可以保证任意$J$个字符串按照这样拼接的顺序是最小的。

然后考虑如何挑选出这$J$个字符串。

考虑逆向DP，即：

$$dp[i][j]=\min (dp[i+1][j],S_i+dp[i+1][j-1])$$

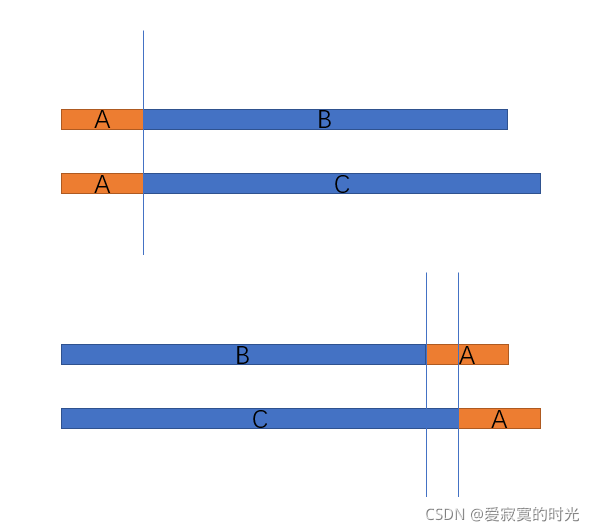
为什么比上面的方程对，考虑下图：

前两个是从后往前DP，$A$即为$S_i$，说明两个字典序的影响完全来自于后面的字符串。

后两个为从前往后DP，此时两个字典序的影响还受$A$字符串的影响，不完全来自于前面的字符串，因此前面字符串的字典序最小不一定是最优拼接答案。