《算法笔记》读书记录DAY_15

最新推荐文章于 2025-12-03 13:56:23 发布

原创最新推荐文章于 2025-12-03 13:56:23 发布 · 105 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构

算法学习专栏收录该内容

63 篇文章

订阅专栏

本文详细介绍了三种计算组合数的方法：递推公式、基于质因子分解的定义式计算以及Lucas定理的应用。适合不同规模数据和素数条件下的组合数求解，包括递推法的适用范围m≤n≤1000，定义式法处理m≤n≤10^6，以及Lucas定理处理大数情况p≤10^18。

CHAPTER_5 数学问题入门

5.8.3组合数的计算（2）

本节我们讨论组合数的第二个问题：如何计算 $C_{n}^{m}%p$ 。下面给出3种方法，它们有各自适合的数据范围，需要根据具体情况使用。一般来说，方法一足够满足需要。

方法一：通过递推公式计算

这种方法方法基于第一个问题中的递推方法。该方法可以很好的支持m<=n<=1000的情况，并且对p的大小和素性没有其他限制。属于很实用的方法。代码如下：

const int maxn = 1001;
int record[maxn][maxn] = { 0 };

int cal(int n, int m, int p) {
    if (record[n][m]) {
        return record[n][m];
    }
    if (n == m || m == 0) {
        record[n][m] == 1;
        return record[n][m];
    }
    else {
        record[n][m] = (cal(n - 1, m) + cal(n - 1, m - 1)) % p;
        return record[n][m];
    }
}

方法二：根据定义式计算

这种方法思路很简单。如果我们能把 $C_{n}^{m}$ 做质因子分解为 $C_{n}^{m}%p=p_{1}^{c1}\times p_{2}^{c2}\times ...\times p_{3}^{c3}%p$ 。我们就可以用4.5.3快速幂的算法计算每一个 $p_{i}^{ci}%p$ ，把各自的结果相乘最后模p。

那么我们怎样质因子分解 $C_{n}^{m}$ 呢？考虑 $C_{m}^{n}=\frac{n!}{m!(n-m)!}$ ，我们可以用5.8.1的算法分别计算n!中含质因子p的个数x、m!中含质因子p的个数y、(n-m)中含质因子p的个数z。最后 $C_{n}^{m}$ 中含质因子p的个数为x-y-z。我们只需枚举1~n中的每个质数，然后计算它们的个数，最后可以将 $C_{n}^{m}$ 分解。

此法可以支持m<=n<=10^6的数据范围，并且对p的大小和素性没有其他限制。代码如下：

//先通过之前介绍过的find_prime()函数打印素数表prime[]

int binary_pow(int a, int b, int p) {        //快速幂 
	if (b == 0)
		return 1;
	else if (b % 2)
		return a * binary_pow(a, b - 1, p) % p;
	else {
		int mul = binary_pow(a, b / 2, p);
		return mul * mul % p;
	}
}


int p_num(int n, int p) {                     //计算n!中质因子p的个数 
	int sum = 0;
	while (n) {
		sum += n / p;
		n /= p;
	}
	return sum;
}


int cal(int n, int m, int p) {                 //根据上述算法计算C(m,n)%p 
	int ans = 1;
	for (int i = 1; prime[i] <= n; i++) {           //prime[]为素数表
		int num = p_num(n, prime[i]) - p_num(m, prime[i]) - p_num(n - m, prime[i]);
		ans *= binary_pow(prime[i], num, p) % p;
	}
	return ans;
}

方法三：Lucas定理

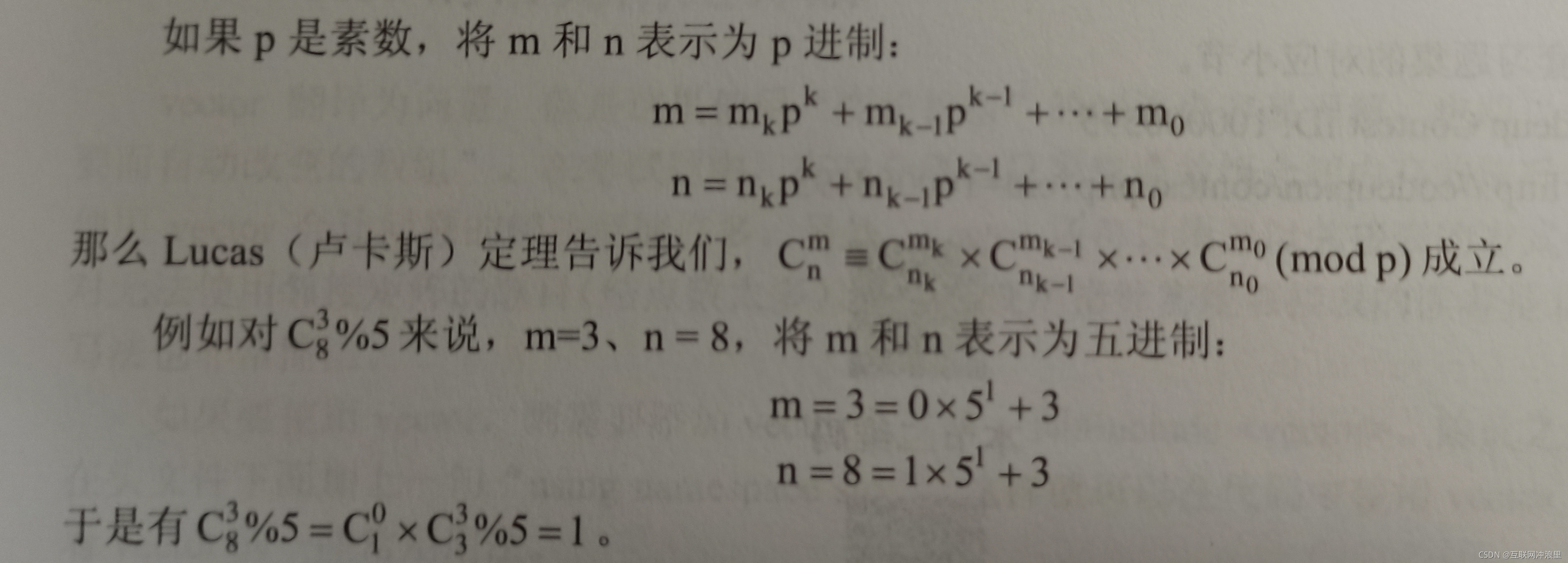
看起来很复杂，那么这个式子意味着什么呢？由于n和m的p进制表示的项数为O(logn)级别。因此Lucas定理意味着将 $C_{n}^{m}%p$ 分解为O(logn)级别个小组和数的乘积的模。

此算法适合处理m<=n<=10^18并且p<=10^18的情况，唯一的要求是p必须为素数。代码如下：

int p;                                            //p为全局变量

int lucas(int n,int m) {
	if(m==0)
		return 1;
	else
		return cal(n%p,m%p)*lucas(n/p,m/p)%p;     //cal()为计算C(n,m)的函数 
}