Go语言数据结构-二叉树

已于 2022-11-04 11:59:33 修改
阅读量949 收藏 2
点赞数 1
CC 4.0 BY-SA版权
分类专栏： Golang 数据结构和算法 文章标签： 数据结构 golang 二叉树
于 2022-10-27 00:32:44 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/jeremy_ke/article/details/127543869
本文主要介绍了二叉树这一数据结构，用Golang语言实现。阐述了二叉树的定义、特点和基本结构，详细讲解了前序、中序、后序和宽度优先遍历的思路及代码。还介绍了搜索、满、完全和平衡二叉树的定义、性质及判断方法，并给出代码实现。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

定义

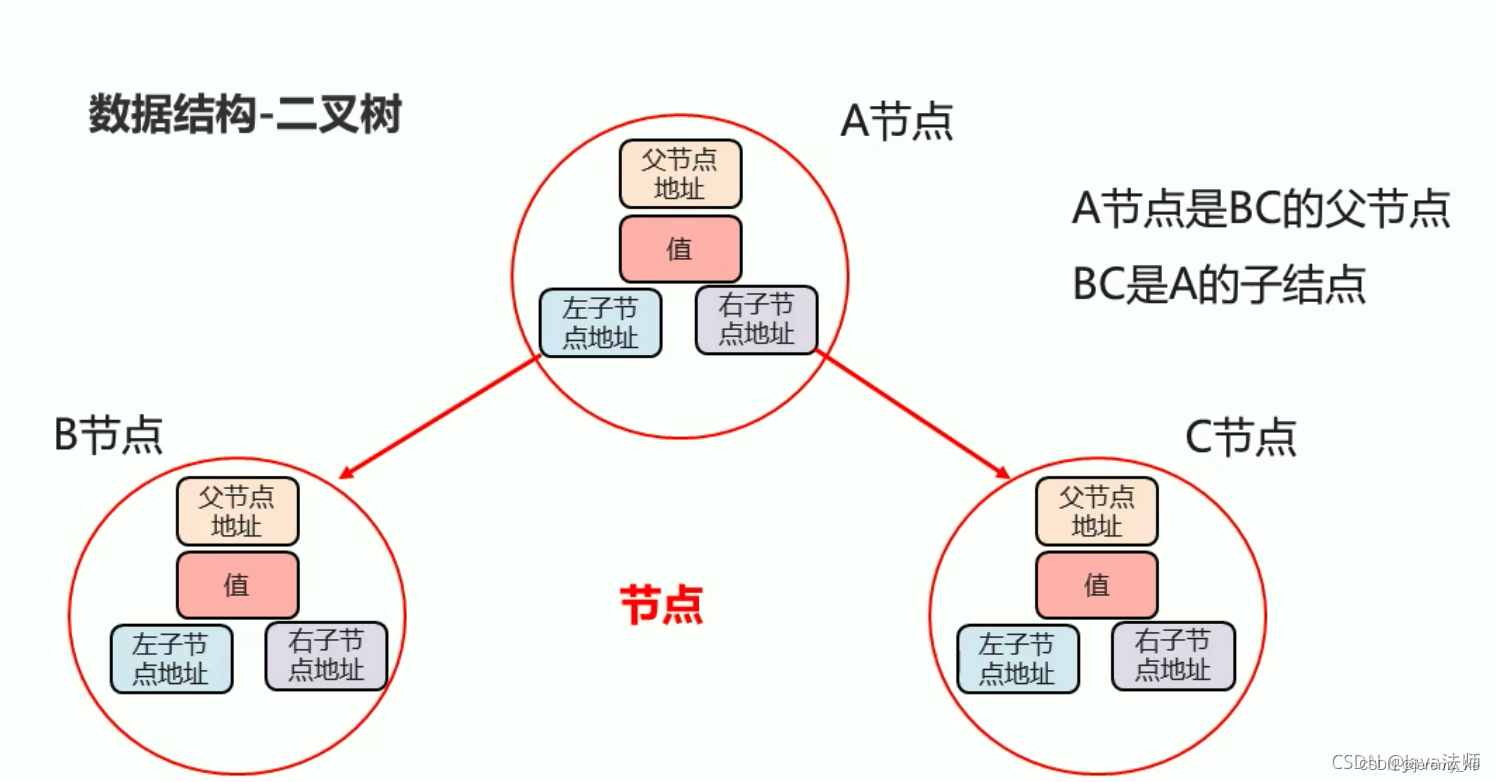
二叉树是一种数据结构，它是由 n(n≥1) 个有限节点组成一个具有层次关系的集合。
根节点：最上面的节点；叶子节点：左右子节点都为nil的节点。
在这里插入图片描述

特点

  • 每个节点有零个或两个子节点；
  • 没有父节点的节点称为根节点；
  • 每一个非根节点有且只有一个父节点；
  • 除了根节点外，每个子节点可以分为多个不相交的子树

基本结构

type Node struct {
	Value int
	Left  *Node
	Right *Node
}

遍历

前序遍历

对每颗子树，均遵循根节点–>左节点–>右节点

递归前序
func preShowTree(head *Node) {
	if head == nil {
		return
	}
	fmt.Println(head.V)//第一次来到节点的时候打印
	showTree(head.Left)
	showTree(head.Right)
}
非递归前序(深度优先遍历)

思路：

  1. 声明一个栈
  2. 从栈中弹出一个节点cur
  3. 打印（处理）cur
  4. 先右后左（如果有），把该节点的子节点压入栈中
  5. 循环执行1->2->3

代码实现：

package main

import (
	"errors"
	"fmt"
)

type Node struct {
	Value int
	Left  *Node
	Right *Node
}

type Stack struct {
	MaxTop int      //栈最大可以存放的数的个数
	Top    int      //表示栈顶的索引id，初始值为-1，最大值为MaxTop-1
	Arr    [7]*Node //数组模拟栈
}

func (s *Stack) Push(pushNode *Node) error {
	if s.Top == s.MaxTop-1 {
		return errors.New("栈满了")
	}

	s.Top++
	s.Arr[s.Top] = pushNode

	return nil
}

func (s *Stack) Pop() (popNode *Node, err error) {
	if s.Top == -1 {
		return nil, errors.New("空栈")
	}
	popNode = s.Arr[s.Top]
	s.Arr[s.Top] = nil
	s.Top--
	return popNode, nil
}

func (s *Stack) List() {
	if s.Top == -1 {
		fmt.Println("空栈")
	}
	for i := 0; i < s.Top+1; i++ {
		fmt.Printf("Arr[%v]=%v\n", i, s.Arr[i])
	}
}

func main() {
	root := &Node{Value: 1}
	left := &Node{Value: 3}
	right := &Node{Value: 4}
	root.Left = left
	root.Right = right
	left1 := &Node{Value: 5}
	right1 := &Node{Value: 6}
	left2 := &Node{Value: 7}
	right2 := &Node{Value: 8}
	left.Left = left1
	left.Right = right1
	right.Left = left2
	right.Right = right2
	showTree(root)
}

func preShowTree(head *Node) {
	if head != nil {
		nodeStack := &Stack{MaxTop: 7, Top: -1}
		nodeStack.Push(head)
		for nodeStack.Top < nodeStack.MaxTop-1 && nodeStack.Top > -1 {
			tmpNode, _ := nodeStack.Pop()
			if tmpNode != nil {
				fmt.Println(tmpNode.Value)
			}
			if tmpNode.Right != nil {
				nodeStack.Push(tmpNode.Right)
			}
			if tmpNode.Left != nil {
				nodeStack.Push(tmpNode.Left)
			}
		}
	}

}

中序遍历

中序:对每颗子树，均遵循左节点–>根节点–>右节点

递归中序
func midShowTree(head *Node) {
	if head == nil {
		return
	}
	showTree(head.Left)
    fmt.Println(head.V)//第二次来到节点的时候打印
	showTree(head.Right)
}
非递归中序

思路：

  1. 申请1个栈
  2. 把每颗子树的整树所有左节点入栈
  3. 依次弹出的过程中，打印该节点，且对该节点的右节点，循环1，2,
  4. 循环执行1->2->3
  5. 打印收集栈中数据

代码实现：

func midShowTree(head *Node) {
	if head != nil {
		nodeStack := &Stack{MaxTop: 7, Top: -1}
		for !nodeStack.IsEmpty() || head != nil {
			if head != nil { //所有左节点压入栈
				nodeStack.Push(head)
				head = head.Left
			} else { //弹出栈的数据，打印节点，且对右子节点循环if的操作
				popNode, _ := nodeStack.Pop()
				fmt.Println(popNode.Value)
				head = popNode.Right
			}
		}
	}
}

后序遍历

后序:对每颗子树，均遵循左节点–>右节点–>根节点

递归后序
func afterShowTree(head *Node) {
	if head == nil {
		return
	}
	showTree(head.Left)
	showTree(head.Right)
    fmt.Println(head.V)//第三次来到节点的时候打印
}
非递归后序

思路：

  1. 申请两个栈（普通栈和收集栈）
  2. 从普通栈中弹出一个节点cur
  3. 把该节点压入收集栈中
  4. 先左后右（如果有），把该节点的子节点压入普通栈中
  5. 循环执行1->2->3
  6. 打印收集栈中数据

代码实现：

func afterShowTree(head *Node) {
	if head != nil {
		nodeStack := &Stack{MaxTop: 7, Top: -1}
		showStack := &Stack{MaxTop: 7, Top: -1}
		nodeStack.Push(head)
		for !nodeStack.IsEmpty() {
			popNode, _ := nodeStack.Pop()
			showStack.Push(popNode) //当前节点压入收集栈
			//左子节点压入普通栈
			if popNode.Left != nil {
				nodeStack.Push(popNode.Left)
			}
			//右子节点压入栈
			if popNode.Right != nil {
				nodeStack.Push(popNode.Right)
			}
		}
		//便利收集栈数据
		showStack.List()
	}
}

宽度优先遍历

思路：

  1. 申请一个队列
  2. 把头结点加入队列
  3. 从队列中弹出一个节点cur，并打印
  4. 先左后右（如果有），把该节点的子节点加入队列
  5. 循环执行2->3

代码实现：

type Queue struct {
	buff    []*Node //队列的的数据存储在数组上
	maxsize int     //队列最大容量
	front   int     //队列头索引，不包括自己（队列头索引值-1）
	rear    int     //队列尾索引
}

//
// Push
// @Description: 压入队列
// @Author: maxwell.ke
// @time 2022-10-25 22:58:58
// @receiver q
// @param n
// @return error
//
func (q *Queue) Push(pushNode *Node) error {
	if q.rear == q.maxsize-1 {
		if q.front == -1 { //头尾都到头了
			return fmt.Errorf("队列已满，PUSH失败")
		} else { ////尾都到头了，头有空，则重置front
			q.front = -1
			q.rear = len(q.buff) - 1
		}
	}
	q.rear++
	q.buff = append(q.buff, pushNode)
	return nil
}

//
// Pop
// @Description: 出队列
// @Author: maxwell.ke
// @time 2022-10-25 23:14:20
// @receiver q
// @return n
// @return err
//
func (q *Queue) Pop() (popNode *Node, err error) {
	if len(q.buff) == 0 {
		return nil, fmt.Errorf("空队列,POP失败")
	}
	popNode = q.buff[0]
	q.buff = q.buff[1:]
	q.front++
	return popNode, nil
}

//
// List
// @Description: 队列遍历
// @Author: maxwell.ke
// @time 2022-10-25 23:13:10
// @receiver q
// @return error
//
func (q *Queue) List() error {
	if len(q.buff) == 0 {
		return fmt.Errorf("空队列")
	}
	for i := 0; i < q.maxsize; i++ {
		if i > q.front && i <= q.rear {
			fmt.Println(q.buff[i-q.front-1].Value)
		} else {
			fmt.Println("nil")
		}
	}
	fmt.Println()
	return nil
}

func wideShowTree(head *Node) {
	nodeQueue := &Queue{buff: make([]*Node, 0, 7), maxsize: 7, front: -1, rear: -1}
	nodeQueue.Push(head)
	for len(nodeQueue.buff) < nodeQueue.maxsize && len(nodeQueue.buff) > 0 {
		cur, _ := nodeQueue.Pop()
		fmt.Println(cur.Value)
		if cur.Left != nil {
			nodeQueue.Push(cur.Left)
		}
		if cur.Right != nil {
			nodeQueue.Push(cur.Right)
		}
	}
}

特殊二叉树

搜索二叉树

定义

每一个子树，左节点比根节点小，右节点比根节点大的二叉树，二叉树的节点无重复值。

判断方法

中序（递归中序或者非递归中序均可）遍历二叉树，如果是升序的即为搜索二叉树。

代码实现（递归中序的方法）：

func isBST(head *Node) bool {
	if head == nil {
		return true
	}
	leftBST := isBST(head.Left)
	if !leftBST {
		return false
	}
	//打印事件改为了比较事件
	if head.Value <= preValue {
		return false
	} else {
		preValue = head.Value
	}

	rightBST := isBST(head.Right)
	return rightBST
}

满二叉树

定义

如果二叉树中除了叶子结点，每个结点的度都为2，则此二叉树称为满二叉树。

性质
  1. 满二叉树中第 i 层的节点数为 2^i - 1 个。
  2. 深度为k的满二叉树必有 2k-1 个节点 ，叶子数为 2k-1。
  3. 满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。
  4. 具有 n 个节点的满二叉树的深度为 log2(n+1)。
判断方法

方法一：根据性质1来判断：

  1. 先求出树的层数i，再统计节点数k
  2. 如果k = 2^i -1，则为满二叉树

方法二：判断左子树为满二叉树且右子树为满二叉树

代码实现：

func isFBT(head *Node) bool {
	if head == nil {
		return true
	}
	leftFBT := isFBT(head.Left)
	if !leftFBT {
		return false
	}
	if (head.Left != nil && head.Right == nil) || (head.Left == nil && head.Right != nil) {
		return false
	}
	rightFBT := isFBT(head.Right)
	return rightFBT
}

完全二叉树

定义

如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

判断方法
  1. 按照宽度优先遍历
  2. 任意一个节点有右子节点无左子节点，则为非完全二叉树
  3. 在条件1不违规的情况下，如果遇到左右子节点不齐全的情况下，后续节点皆为叶子节点，如果后续存在非叶子节点，则为非完全二叉树。

代码实现：

func isCBT(head *Node) bool {
	if head == nil {
		return true
	}
	var (
		leaf = false //是否遇到左右子节点不齐全的情况
		l    *Node
		r    *Node
	)
	nodeQueue := &Queue{buff: make([]*Node, 0, 8), maxsize: 8, front: -1, rear: -1}
	nodeQueue.Push(head)
	for len(nodeQueue.buff) < nodeQueue.maxsize && len(nodeQueue.buff) > 0 {
		popNode, _ := nodeQueue.Pop()
		l = popNode.Left
		r = popNode.Right

		//如果遇到了不双全的节点后，又发现当前节点有子节点 或者 有右节点但无左节点
		if (leaf && (l != nil || r != nil)) || (l == nil && r != nil) {
			return false
		}

		if l != nil {
			nodeQueue.Push(l)
		}
		if r != nil {
			nodeQueue.Push(r)
		}
		if l == nil || r == nil { //左右节点不双全，则后续为叶子节点
			leaf = true
		}
	}
	return true
}

平衡二叉树

定义

对于任何一个子树来说，左树高度和右树高度差不超过1

判断方法

A && B && C
A: 左子树为平衡二叉树
B: 右子树为平衡二叉树
C: abs(左高-右高) <= 1
代码实现：

func isALV(head *Node) bool {
	return process(head).IsBalanced
}

type ReturnType struct {
	IsBalanced bool
	Height     int
}

func process(x *Node) *ReturnType {
	if x == nil {
		return &ReturnType{IsBalanced: true, Height: 0}
	}
	leftData := process(x.Left)
	rightData := process(x.Right)
	height := max(leftData.Height, rightData.Height) + 1 //当前节点的高度
	isBalanced := leftData.IsBalanced && rightData.IsBalanced && math.Abs(float64(leftData.Height-rightData.Height)) <= 1
	return &ReturnType{IsBalanced: isBalanced, Height: height}
}

func max(a, b int) int {
	maxNum := a
	if a < b {
		maxNum = b
	}
	return maxNum
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值