Go语言数据结构-堆

定义

堆是完全二叉树，且根节点比子节点都大的二叉树称为大根堆；反之称为小根堆。
堆的英文是heap；heapSize = 节点个数

基本属性

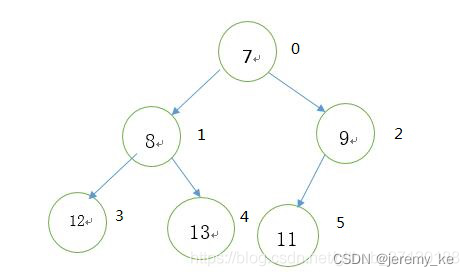
i位置的左子节点是2i+1
i位置的右子节点是2i+2
i位置的父节点是(i-1)/2

应用场景

堆排序

基本结构和操作

尾部添加节点（heapInsert）

问题：
数组接收一个数，使其形成一个新的堆？
思路：

1. heapSize加1，把新数放到堆尾的节点上。
2. 和父节点比较，如果父节点比该数小就交换，以此类推，直至父节点比其大或者没有父节点了。

代码实现：

func heapInsert(arr []int ,index int)  {
    for arr[index] > arr [(index -1) /2] {//比父节点大，就和父节点交换
		swap(arr,index,(index-1)/2)
		index = (index-1)/2
    }
}

func swap(arr []int,a,b int)  {
    arr[a] = arr[a] ^ arr[b]
    arr[b] = arr[a] ^ arr[b]
    arr[a] = arr[a] ^ arr[b]
}

头部取出根节点(heapify)

问题：
如何取出大根堆的头结点？
思路：

1. 取出头节点，把最后一个节点的数放在头结点上，heapSize减1。
2. 然后把头结点的数和两个子节点中最大的数比较，比较大子节点还大就交换位置，以此操作，直至没有子节点或者比子节点都小。这个过程叫做heapify.

代码实现：

func heapify(arr []int, index, heapSize int) {
	left := index*2 + 1
	for left < heapSize {
		//取出2个子节点中最大的节点位置
		biggerChild := left
		if left + 1 <heapSize && arr[left+1]>arr[left]{
			biggerChild = left +1
        }
		//把当前节点的数和子节点较大的数比较
		if arr[biggerChild] < arr[index]{
			biggerChild = index
        }
		if biggerChild == index {
			break
        }
		//交换位置
		swap(arr,biggerChild,index)
		index = biggerChild
		left = index * 2 +1
	}
}

func swap(arr []int,a,b int)  {
	arr[a] = arr[a] ^ arr[b]
	arr[b] = arr[a] ^ arr[b]
	arr[a] = arr[a] ^ arr[b]
}

综合应用

把一个连续区域内，把i位置的节点的数修改后，依然是堆？
思路：i位置数变小了，heapify过程；i位置数变大了，heapInsert过程。依然是堆结构。

代码实现：

func edit(arr []int, index, value int) {
	if index >= len(arr) || index <= 0 {
		return
	}
	heapSize := len(arr)
	if value < arr[index] {
		arr[index] = value
		heapify(arr, index, heapSize)
		return
	}
	if value > arr[index] {
		arr[index] = value
		heapInsert(arr, index)
		return
	}
	return
}

堆排序(heapSort)

思路：

1. 先让整个数组都变成大根堆结构，建立堆的过程:
   1)从上到下的方法，时间复杂度为O(N*logN)
   2)从下到上的方法，时间复杂度为O(N)
2. 把堆的最大值和堆末尾的值交换，然后减少堆的大小之后，再去调整堆
3. 一直周而复始，时间复杂度为O(N*logN) 3，堆的大小减小成0之后，排序完成

代码实现：

func heapSort(arr []int) {
	if len(arr) < 2 {
		return
	}
	//把数组放入一个大根堆里面
	for i := 0; i < len(arr); i++ {
		heapInsert(arr, i)
	}
	heapSize := len(arr)
	//0位置的数和最后位置数交换
	swap(arr, 0, heapSize-1)
	heapSize--
	//再把0位置数heapSize
	for heapSize > 0 {
		heapify(arr, 0, heapSize)
		swap(arr, 0, heapSize-1)
		heapSize--
	}
}