自动驾驶和电动卡车适应公路地形的最佳经济驾驶控制:能量最小化和电池寿命延长
摘要:本文开发了一种模型,通过考虑车辆前方的地形和交通信息来实时规划电动卡车的节能速度轨迹。 在这个实时控制模型中,首先开发了一种新颖的状态空间模型来捕获车辆速度、加速度和充电状态。 然后通过利用问题结构的交替方向乘法器 (ADMM) 来制定和解决能量最小化问题。 进一步采用模型预测控制(MPC)框架来实时处理地形和交通不确定性。 最后对所提出的生态驾驶算法的性能及其对电池退化的影响进行了实证研究。 仿真结果表明,与基准方案相比,采用该方法的能耗降低高达5.05%,电池寿命延长100%以上。
索引术语 — 交替方向法乘子法(ADMM)、自动驾驶和电动卡车、电池寿命延长、能量最小化、重型 (HDT) 卡车、模型预测控制 (MPC)、速度控制。
| 名词 | 解释 |
|---|---|
| HDT | 重型卡车 |
| BE | 电池电动 |
| ICE | 内燃机 |
| EM | 电动机 |
| 变量 | 解释 |
|---|---|
| βairβ_{air}βair | (1/2)ρairAfCD(1/2)ρ_{air} A_fC_D(1/2)ρairAfCD |
| Fiair(t)F_i^{air}(t)Fiair(t) | 空气阻力 =βair∗vi2β_{air}*v_i^2βair∗vi2 |
| Fires=βi(0)F_i^{res} = β_i^{(0)}Fires=βi(0) | 路面摩擦阻力和重力阻力组成的阻力 |
| Fitrack(t)F_i^{track}(t)Fitrack(t) | 电动机产生的驱动力 |
| pi(t)p_i(t)pi(t) | 电功率 |
| β+β^+β+ | 车辆放电效率,β+β^+β+是个(0,1)的值吧 |
| 1/β−1/β^−1/β− | 车辆充电效率,β−β^-β−是个 >1 的值吧 |
| C | 电池标称容量(Ah) |
| U | 假设在常用 SOC 范围内恒定的电池端电压(v) |
| ξ\xiξ | 总容量衰减 |
| QQQ | 充电/放电过程中的安时 (Ah) 电荷, |
| ξ′\xi 'ξ′ | 容量衰减率,单位是电池每充放 1Ah 时衰减的 Ah 数 |
| SOCavgSOC_{avg}SOCavg | 平均 SOC(剩余电量百分比) |
| SOCdevSOC_{dev}SOCdev | SOC 平均值的归一化标准偏差,啥意思? |
| DODDODDOD | 放电深度百分比 |
I. INTRODUCTION
在美国,重型卡车 (HDT) 占所有货运量的 70%,占交通运输部门温室气体 (GHG) 排放量的 20% [1]。 因此,HDT 的脱碳对于发展可持续交通至关重要,而能够实现这一目标的一项技术是电池电动 (BE) HDT [2]、[3]。 近年来重卡电动化发展迅速,据麦肯锡预测,到2030年BE卡车销量将占全球卡车销量的15%[4]。 然而,BE HDT的发展受到目前锂离子电池技术的极大限制,特别是能量密度低和循环寿命短[5]。
解决这一技术瓶颈的一种方法是开发能量密度和循环寿命大幅提高的下一代电池[6],但通常需要数十年的时间,无法满足立即使用的要求。 另一种方法是通过智能能量管理和速度控制策略来减少车辆能耗和电池老化,这要归功于经济驾驶控制技术。 事实上,已经为乘用车 [7]-[10] 和 HDT [11]-[15] 的节能驾驶开发了许多算法。 在[7]中,节能驾驶技术被讨论并表述为一个最优控制问题,其中包括在时间和距离范围内最小化车辆消耗,然后导出最优轨迹的封闭式解。 徐等人。 [8]提出了一种针对联网自动驾驶车辆的交通信号控制和车辆速度优化的协作方法,该方法同时优化了交通信号配时和车辆的速度轨迹。 Zeng和Wang[9]提出了一种车辆在给定路线上行驶且有多个停车标志、红绿灯等的最优速度规划解决方案。 马里科普洛斯等人。 [10]解决了许多自动车辆在进入高速公路减速区之前的速度控制问题。 尽管涉及交通信号、限速等不同的驾驶场景[7]-[10],但出于模型简化的目的,乘用车建模通常忽略了道路地形和空气动力学的影响,这极大地影响了重卡的能耗 其特点是体型大、重[16]。 一些文献通过优化分配驱动功率,为混合动力电动汽车(HEV)开发了电池老化意识能源管理策略[17]-[20],但如何以节能的方式驱动电动汽车(EV),同时最大限度地减少电池老化仍然存在 仍然是一个悬而未决的问题。 事实上,由于长途行驶的需求,电池能量密度低、循环寿命短等缺点随着BE HDT的使用而被大大放大。 因此,BE HDT 最优控制尤其需要考虑电池老化的经济驾驶算法。
HDT 的环保驾驶控制主要集中在内燃机(ICE)驱动的 HDT 上。Hellström 等人。 [11]开发了一种预测巡航控制器,其中使用动态规划(DP)方法来数值求解最优控制问题。 在[11]中,开发了一种预处理算法来缩小DP的搜索空间,从而降低算法复杂度以实现实时操作。 郭和王[12]研究了卡车排的速度规划和跟踪控制问题,提出了卡车排协调的两层分层框架:用于计算途中速度曲线的速度规划层和用于车辆速度的控制层 追踪。 赫尔德等人。 [13] 为城市驾驶中不同速度限制的应用开发了节能驾驶算法,而 Borek 等人。 [14]通过使用基础设施到车辆通信,制定了涉及交通和信号交叉口导航的经济最优控制策略。 传统HDT的速度控制通常涉及档位选择(整数)的优化,同时经常引入DP方法[11]、[12]、[14]、[15]。 与传统HDT相比,BE HDT的速度控制通常涉及非整数优化,从而为引入比DP方法更高效的优化算法提供了机会。 据作者所知,这是第一篇专注于 BE HDT 的最佳生态驾驶控制的文章,考虑了能源消耗和电池老化的影响。
在这项工作中,做出了三项主要贡献。 首先,构建了一种新颖的状态空间模型来捕获车速、加速度和电池充电状态 (SOC) 的依赖性。 基于该模型,进一步制定了涉及道路地形和周围交通的能量最小化优化问题。 然后,考虑地形和交通不确定性,开发了基于乘子交替方向法(ADMM)的模型预测控制(MPC)方法,从而实现高效的实时速度控制。 最后,通过引入面向电动汽车的(电池)老化模型,系统评估了速度控制算法对电池退化的影响,并进一步进行了实证研究,以验证有周围交通和没有周围交通的情况下经济驾驶策略的性能。
本文的其余部分组织如下。 第二节描述了卡车系统动力学的状态空间模型。 第三节定义了能量优化问题并开发了优化和控制算法。 第四部分显示了基于所开发方法的卡车能耗结果,第五部分显示了电池老化评估结果。 最后,第六节总结了本文。
II. STATE-SPACE EQUATION MODELING
在本节中,构建了连接车辆速度、加速度和能量消耗的状态空间模型,其中车辆速度和电池SOC分别是模型状态和输出。 建模过程详细介绍如下。
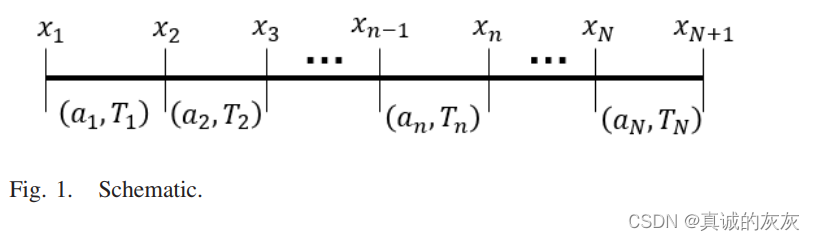
令总行程分为N个等距的单位长度段,段 iii 从 tit_iti 开始。 原理图如图1所示,段变量的定义如表1所示。

状态方程模型的定义:
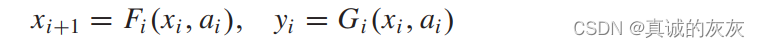
其中 Fi(⋅,⋅)F_i(·,·)Fi(⋅,⋅) 是状态转换,Gi(⋅,⋅)G_i(·,·)Gi(⋅,⋅) 是输出函数。
A. State Transition Function
需要注意的是,为了便于推导,图1中各路段的长度被视为单位长度“1”,但在实证研究(第四节)中将根据实际情况对其进行参数化。 在这种情况下,xi、ai和Tix_i、a_i 和 T_ixi、ai和Ti 的关系为
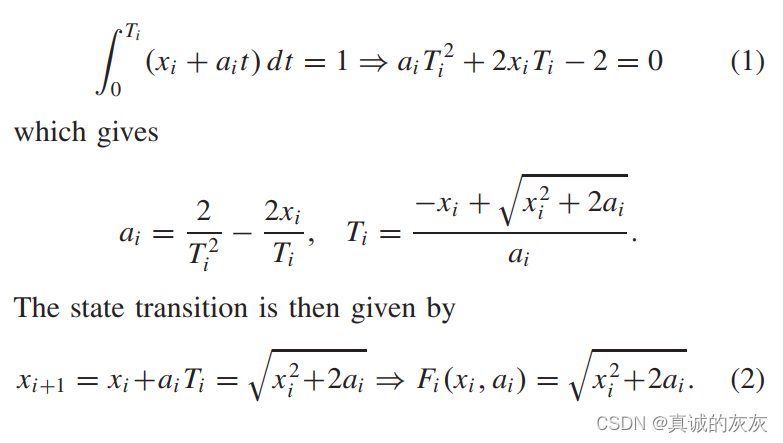
B. Output Function
1)各路段内的SOC变化:SOC表示电池剩余容量与标称容量的比值,因此,各路段内的SOC变化定义为
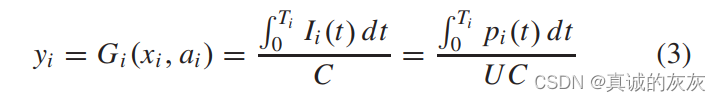
其中 C 代表电池标称容量,U 代表假设在常用 SOC 范围内恒定的电池端电压 [21]
2)车辆纵向动力学:描述车辆纵向动力学的方程为
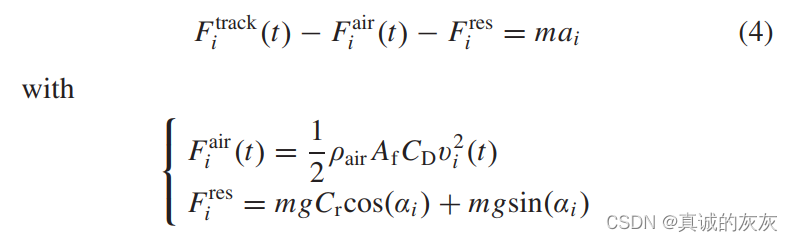
其中 mmm 是车辆质量; Fitrack(t)F_i^{track}(t)Fitrack(t) 是电动机(EM)产生的驱动力; Fiair(t)F_i^{air}(t)Fiair(t) 为空气阻力,ρairρ_{air}ρair 表示空气质量密度,AfA_fAf 表示车辆正面面积,CDC_DCD 表示气动阻力系数; FiresF_i^{res}Fires 为由路面摩擦阻力和重力阻力组成的阻力,CrC_rCr 表示滚动阻力系数,αiα_iαi 表示第 iii 段的坡度。 为了简化推导过程,假设 βair=(1/2)ρairAfCDβ_{air} = (1/2)ρ_{air} A_fC_Dβair=(1/2)ρairAfCD,Fires=βi(0)F_i^{res} = β_i^{(0)}Fires=βi(0),其中 βairβ_{air}βair 与路段条件无关,而 βi(0)β_i^{(0)}βi(0) 取决于每个路段的坡度。
3)输出函数建模:履带力 Fitrack(t)F_i^{track}(t)Fitrack(t) 由电池能量产生。 当电池放电时,pi(t)>0p_i(t) > 0pi(t)>0,电功率根据下式转换为正履带力:
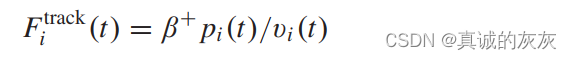
其中 β+β^+β+表示车辆放电效率。
当电池通过动能 pi(t)<0p_i(t) < 0pi(t)<0 充电时,电机产生负驱动力,如下所示
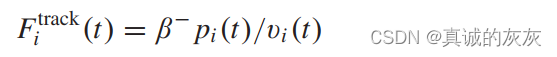
其中 1/β−1/β^−1/β− 表示车辆充电效率。 这里,我们假设所有的制动都可以通过电制动来实现,并且是再生制动; 因此,不包括摩擦制动。 这一假设与实践一致,即最大限度地减少摩擦制动器的使用,以提高能源效率并减少磨损[22]。
那么,电池的瞬时功率输出可表示为
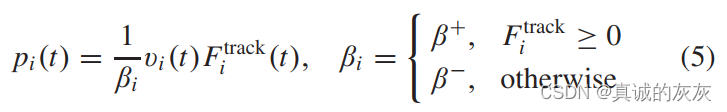
其中βiβ_iβi包括电池充电/放电、交流/直流转换器、电动机和变速箱的效率。 变速箱造成的传动能量损失很小,传动能量效率设定为接近100%的常数[15]。 电磁效率随着电机的扭矩和转速而变化,根据本研究中的电机效率图和车辆速度限制,也可以将其视为常数。 电动机效率的详细简化过程参见附录 A。
注意,由式(4)可以验证驱动力的符号,因此,βiβ_iβi 等于 β+β^+β+ 还是 β−β^−β− 由(xi,ai)(x_i,a_i)(xi,ai)的向量决定,即驱动力可以为正,也可以为负, 在每个路段内从正值变为负值,反之亦然。 这四种情况导致了输出函数的不同建模过程,详见附录B。
一般来说,输出函数可以表示为
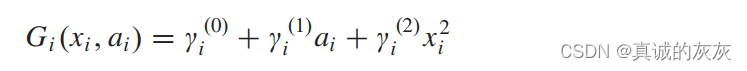
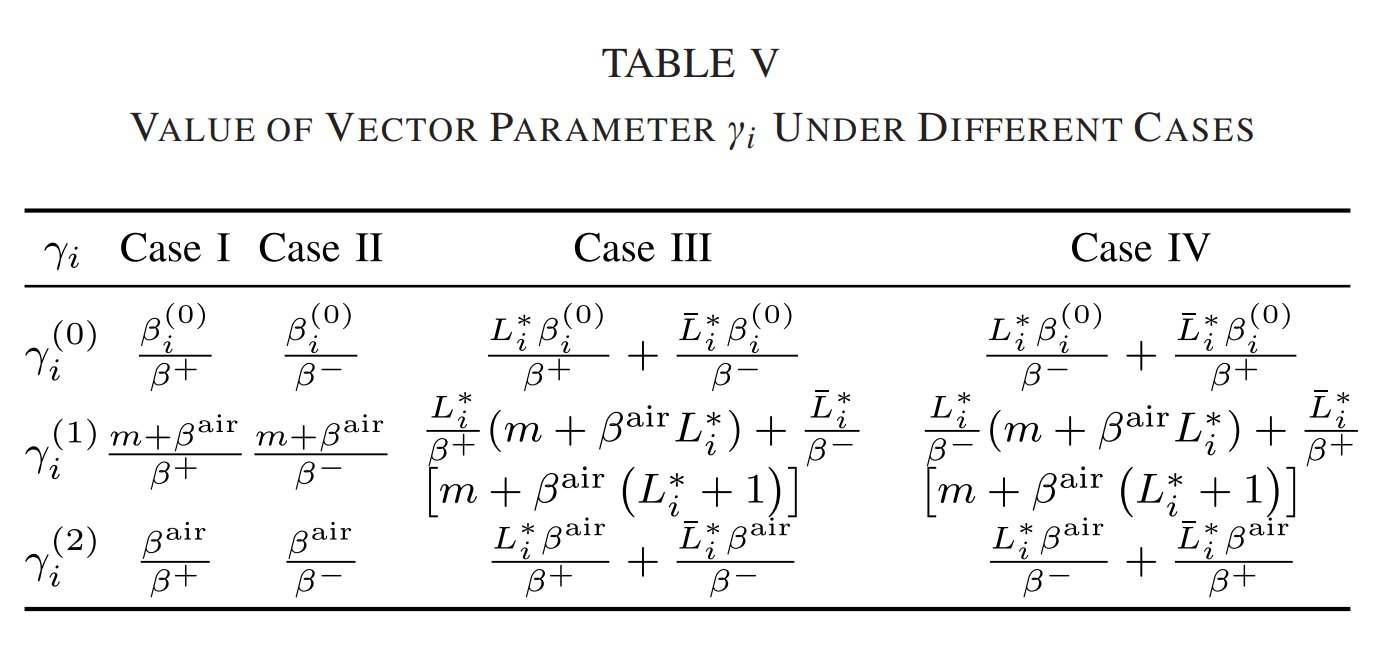
其中向量 γi(xi,ai)\gamma _i(x_i, a_i)γi(xi,ai) 的表达式总结于 表 V(附录 B) 中。

III. FORMULATION AND SOLUTION OF THE ENERGY MINIMIZATION PROBLEM
A. Problem Formulation of Energy Minimization
总能量消耗 (E) 由累积 SOC 变化给出。 在这种情况下,
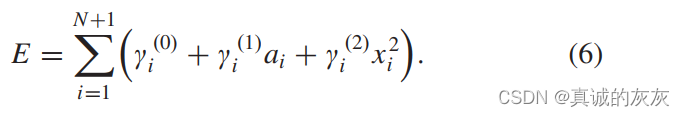
由(1)和(2)有
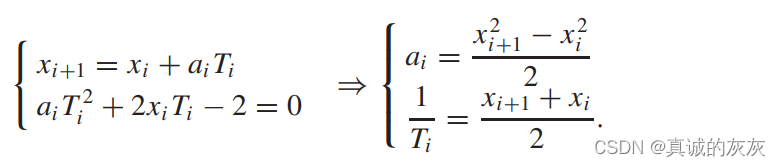
将 aia_iai 代入总能量表达式中,有
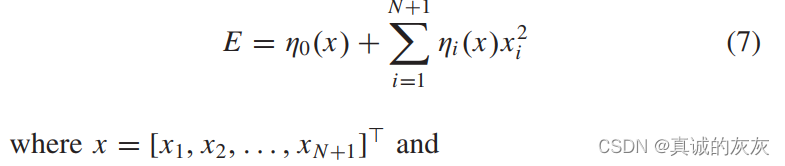
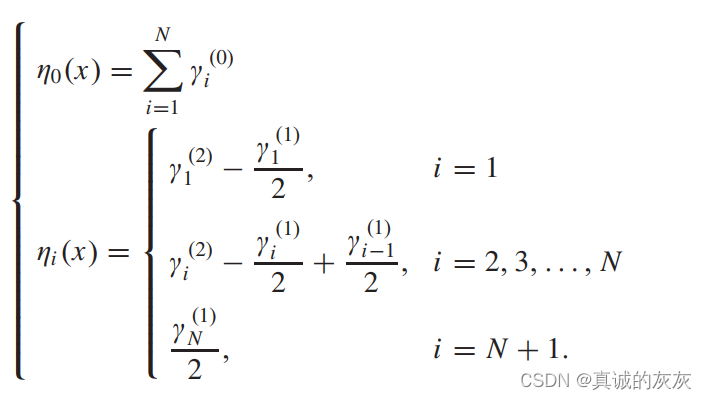
最小能量控制是在总行程时间约束 τ\tauτ 的约束下最小化能量消耗,因此优化问题 PMEP^{ME}PME 表述为
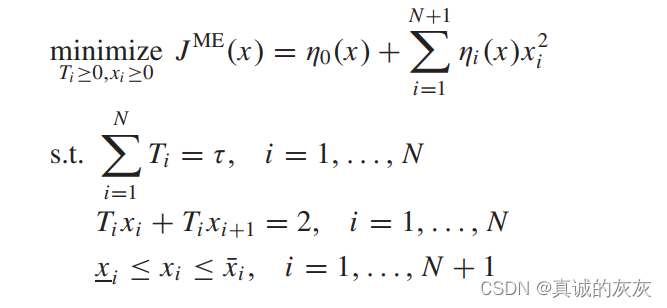
其中 xi‾\underline{x_i}xi 和 xi‾\overline{x_i}xi 分别是速度限制的下限和上限,并且可以通过使速度限制适应周围的交通来轻松引入交通信息。 请注意,PMEP^{ME}PME 涉及两组变量,包括要优化的速度 xxx 和行程时间 TTT。 虽然上面的优化是非凸的,但对于固定 TTT 优化 xxx 可以很容易地解决。 对于固定的 xxx,求解满足约束的 TTT 相当于求解线性方程。 由此,可相应推导出 xxx 和 TTT 交替求解的方法.
备注:第二个约束的解释:(xi+xi+1)2∗Ti=s=1\frac{(x_i+x_{i+1})}{2}*T_i=s=12(xi+xi+1)∗Ti=s=1
B. ADMM-Based Optimal Solution
ADMM 是一种简单但功能强大的算法,非常适合 PMEP^{ME}PME 中描述的分布式优化问题。 它采用分解协调过程的形式,其中协调小型局部子问题的解决方案以找到大型全局问题的解决方案。 ADMM 可以被视为将对偶分解和增广拉格朗日方法的优点结合起来进行约束优化的尝试[23]。
与乘法器方法一样,增广拉格朗日是通过放宽 PMEP^{ME}PME 中的约束而形成的:
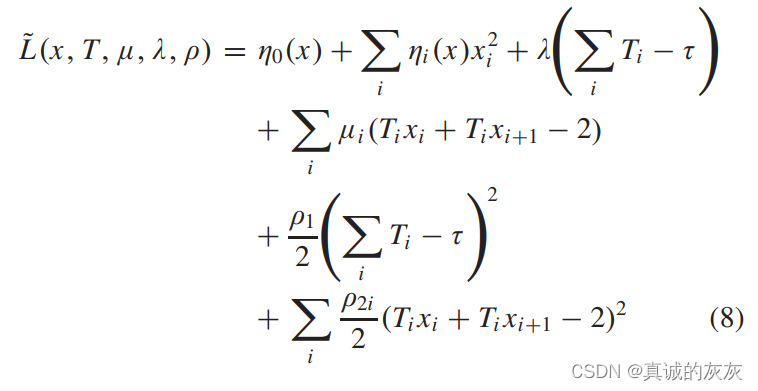
其中 μ=[μ1,μ2,...,μN]Tμ = [μ_1, μ_2, ... , μ_N]^Tμ=[μ1,μ2,...,μN]T 和 λλλ 是与 PMEP^{ME}PME 中的约束相关的拉格朗日乘数,ρ=[ρ1,ρ21,ρ22,⋅⋅⋅,ρ2N]Tρ = [ρ_1, ρ_{21}, ρ_{22,} ···, ρ_{2N}]^Tρ=[ρ1,ρ21,ρ22,⋅⋅⋅,ρ2N]T 是惩罚系数。
最小化关于 (x,T)(x, T)(x,T) 的拉格朗日 (8) 是很重要的。 如果分别求解 x和Tx 和 Tx和T,则难度可以大大降低,从而产生求解 PMEP^{ME}PME 的迭代方法。 特别地,当速度轨迹 xxx 固定时,η0(x)η_0(x)η0(x)和ηi(x)η_i(x)ηi(x)确定。 因此,方程(8)可以表示为 TTT 的二次函数
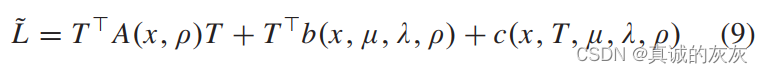
其中,T=[T1,T2,⋅⋅⋅,TN]T,A∈RN×NT = [T_1, T_2, ···, T_N]^T ,A \in R^{N×N}T=[T1,T2,⋅⋅⋅,TN]T,A∈RN×N为二次项的系数矩阵,b∈RNb \in R^Nb∈RN 为一阶项的向量系数,c∈Rc \in Rc∈R 为常数。 最小化关于 TTT 的拉格朗日函数可以以封闭形式求解。 求解 PMEP^{ME}PME 的 ADMM 算法如算法 1 所示。

请注意, (10) 将 x(n)x^{(n)}x(n) 更新为 x(n+1)x^{(n+1)}x(n+1) 的 可以通过标准求解器求解,或者对于大型问题,通过一阶(梯度)更新可能更容易求解。
另请注意,随着速度轨迹 xxx 逐渐变化,驱动力的符号不会突然变化。 路段 iii 内的正驱动力与案例 III(附录 B)一样逐渐变化,最后变成负驱动力。 换句话说,每个路段驱动力的符号变化实际上代表了零驱动力点的移动(参见附录B中的图16)。 驱动力的连续性决定了可行解中能量消耗的连续性。

假设存在可行解 x0x_0x0,并据此确定向量参数 γi(x0)\gamma_i(x_0)γi(x0),则有 limx→x0γi(x)=γi(x0)\textstyle \lim_{x \to x_0}\gamma_i(x) = \gamma_i(x_0)limx→x0γi(x)=γi(x0)。 因为 ηi(x)η_i(x)ηi(x) 由 γi(x)γ_i(x)γi(x) 组成,所以也会有 limx→x0ηi(x)=ηi(x0)\textstyle \lim_{x \to x_0}\eta_i(x) = \eta_i(x_0)limx→x0ηi(x)=ηi(x0)。 由于 x0x_0x0 可以是任意可行解,因此目标函数在 xxx 的可行解中连续,保证了算法的局部收敛。 在我们的模拟中,观察到收敛大约(或平均)在 50-100 次迭代中发生。
C. MPC-Based Vehicle Speed Control
MPC 是一种包含实时操作条件的滑动窗口闭环控制。 为了实现最佳电池电动重载车辆控制,MPC解决了N段开环控制并仅实现第一段的控制[24]。 图2展示了MPC框架的信息流。

基于云的交通信息和态势感知平台将更新的信息发送到车载控制器,包括道路海拔、限速、事故和前方紧急情况。 基于云平台的交通信息和本地传感结果(例如卡车前方汽车的距离),嵌入式 ADMM 算法计算出少量有限路段内的最佳速度和行程时间,例如 N = 30. 卡车运行时仅执行第一段的速度。 请注意,本研究中假设车载控制器所需的准确道路地形和前车速度可用。 道路坡度可以通过融合 GPS 和车辆实时数据以及之前在同一路段上运行的测量值来估计 [25]。 前面的车辆轨迹可以由前面的车辆规划或计算并传达给后面的车辆[7]、[8]、[12]、[13],或者它们可以由后面的车辆本身通过探索过去和现在的测量来计算 机载传感器收集的距离和相对速度[26],[27]。
IV. CASE STUDY
对瑞典南泰利耶市和北雪平市之间的 E4 高速公路的道路数据进行了模拟[11]。 道路坡度和海拔高度如图3所示。

建模的电动卡车是特斯拉半挂车和拖车。 卡车和电池组[2]的规格如表 II 所示。 请注意,卡车有四个独立的电机分别驱动前四个轮,每个电机均由标称电压和容量分别为 800 V 和 312.5 Ah 的电池组供电。
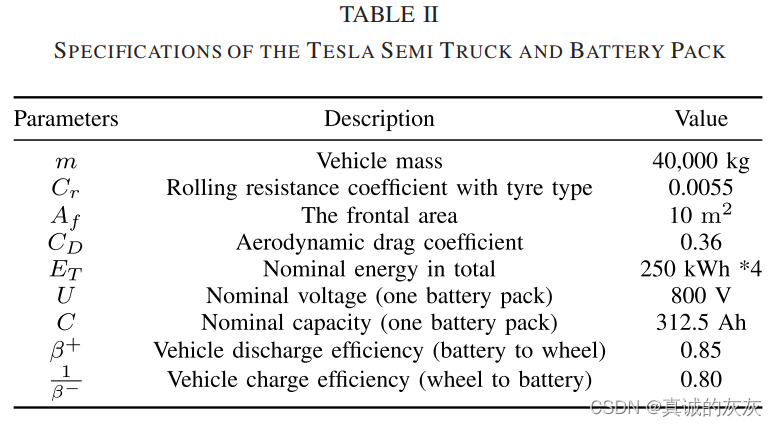
算法参数初始化如下。 每段路段长度l设置为50 m,路段数量N设置为30。每段路段长度设置为50 m,其值可根据实际情况进行调整,经实践证明是可行的。 实践中可行[11],[28]。 因此,预测层位为1500 m。 速度下限设置为 0 公里/小时。 在没有交通的情况下,速度上限设置为欧盟法定最高90公里/小时,速度下限设置为75公里/小时[11],而在有交通的情况下,速度受到周边交通情况的限制。 在MATLAB 2020a环境下进行仿真,基于Macbook Pro,处理器为8核Intel Core i9 @2.4 GHz,内存为32 GB。
A. Optimal Speed Control Without Traffic Involved
在这种情况下,行程时间 τ\tauτ 被设置为等于使用85km/h匀速行驶相同距离的行程时间。
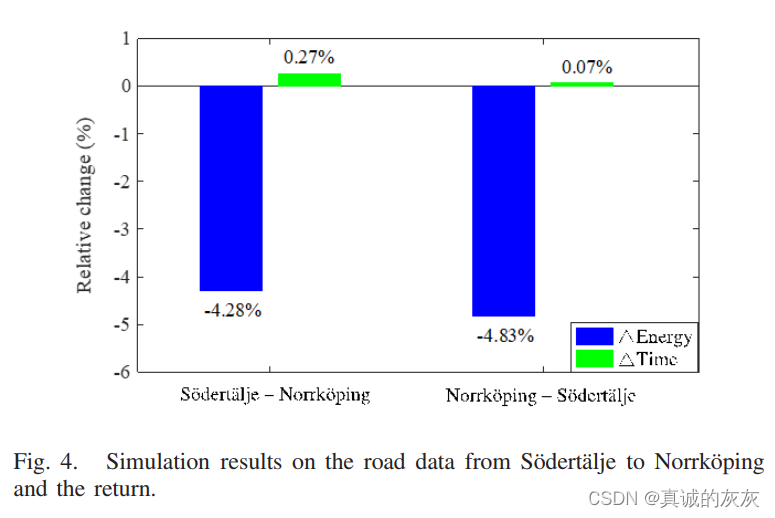
1)总体性能:根据南泰利耶和北雪平之间的道路数据进行了两次仿真,以比较 ADMM 控制器和匀速巡航控制(CC)控制器的性能。 CC速度设置为85 km/h,两个控制器之间的能耗和行程时间的相对变化如图4所示。负值表示ADMM控制器的值低于CC。 结果表明,与 CC 相比,ADMM 控制器从南泰利耶到北雪平节省了 4.28% 的能量,返回时节省了 4.83% 的能量,而这两个控制器之间的跳闸时间在两个方向上彼此相似。
2)性能比较:由于尚未发表关于电动重卡节能驾驶的工作,因此与传统卡车的节能驾驶算法进行了比较[11],其中提出了DP和比例积分控制(PIC) 。 此外,直接引入[11]中的最佳速度轨迹进行性能比较。 根据[11],PIC 是 Scania 提供的标准控制器。 所有可能影响车辆能耗的参数设置与[11]中的相同。 图 5 展示了基于[11,图 11,图 11] 中的道路坡度 ADMM、DP、PIC 和 CC 之间的比较结果。 7和9]。 CC 的速度值设置为与 PI 的行程时间相同。 对于每种道路场景,ADMM 相对于其他方法的能耗和行程时间(SOC 和 T)的相对变化也如图 5 所示。
由于车辆的充放电效率小于1,再生制动只能再生部分消耗的能量。 此外,卡车前进也需要消耗能量来克服各种阻力,这种能量消耗进一步降低了再生制动的效率。 因此,可以通过避免任何不良制动来减少能量消耗。
图5(a)显示重卡基于ADMM保持恒定速度,除了在下坡路段时,卡车先减速,然后加速,最后再次减速至恒定速度。 如图 5(b)所示,基于 ADMM 的下坡能耗接近于零,这表明卡车以最节能的方式向前移动,几乎没有不良制动,而图 5 中观察到了更多的制动事件 (b) 对于所有其他方法,包括 DP、PIC 和 CC。 请注意,传统卡车在上坡时需要降档(减速)以增加驱动力[参见图5(a)中基于DP和PIC的速度轨迹],这导致下坡时不期望的加速和制动[参见DP - 以及图 5(b) 中基于 PIC 的能耗] 以满足跳闸时间要求。 由于采用电机驱动的BE HDT可以在不减速且高速的情况下上坡,因此比传统卡车在下坡时为改善能耗留下了更广阔的改进空间。 这种文献中从未揭示过的现象表明,BE HDT 比 ICE HDT 能以更节能的方式适应道路地形。 在每种情况下,CC 的表现最差,因为它使用了最不理想的制动,因此在下坡时为了保持匀速消耗了最多的能量。 图 5(b)中的能耗结果表明,在相似的跳闸时间下,基于 ADMM 的 BE HDT 的能耗分别比基于 DP 和 PIC 的 ICE HDT 少 1.72% 和 1.78%,以及 1.93%。 比基于 CC 的 BE HDT 能量更少。

图5(c)显示了在具有长下坡路段的道路上的最佳速度轨迹,其中BE HDT在速度上限内制动是不可避免的。 在这种情况下,ADMM 使用较少的制动,因此比其他方法消耗更少的能量 [图 5(d)]。 显然,BE HDT 的驾驶特性与 ICE 驱动的 HDT 有很大不同。 能耗结果表明,在保持相似行程的情况下,基于 ADMM 的 BE HDT 分别比基于 DP 和 PIC 的 ICE HDT 减少了 2.22% 和 2.99% 的能耗,比基于 CC 的 BE HDT 减少了 9.02% 的能耗。 请注意,在这两种情况下,ADMM 比 DP 节省更多能源的原因主要是由于车辆类型不同(例如,BE HDT 与 ICE HDT)。 如果两个控制器都是为 BE HDT 开发的,则预计能耗值会相似。

3)不同速度上限的性能:速度上限设置为90公里/小时,以遵循欧盟法定最高速度限制。 然而,在某些情况下,这个速度限制可能会被打破,如图 5( c ) 中的 ICE HDT 所做的那样。 图6显示了速度上限设置为90、92和95 km/h时的优化结果。 对于车速一般小于速度上限的情况,不同速度约束下的速度轨迹是相似的[图 2]。 [6(a)],导致类似的能量消耗轨迹,从而导致类似的 SOC 减少的相对变化,如图 6(b) 所示。

对于达到每种情况对应的最大速度的情况,其他路段的速度轨迹仍然彼此相似,以减少不必要的制动[图6©]。 虽然速度上限为90公里/小时的能耗比不同速度限制的能耗要小一些,但能耗轨迹仍然相似[图6(d)],表明基于 ADMM 的控制器针对不同速度上限的高性能。

4)车辆参数不确定性下的性能:由于构建车辆能耗模型时电池和电动机模型被简化为恒定效率,因此ADMM控制器针对不确定车辆充电(1/β−1/β^−1/β−)/放电(β+β^+β+)的性能从而评估效率。 假设 1/β−1/β^−1/β− 和 β+β^+β+ 的标准差分别为 0.02 和 0.025。 此外,在此假设下,1/β−1/β^−1/β− 和 β+β^+β+ 的 3σ 基于规则的区间分别为 [0.74, 0.86] 和 [0.775, 0.925],表明放电/充电效率的不确定性超过15%。
基于假设的标准偏差生成十组放电/充电效率。 ADMM 控制器每次都以一种效率集运行并优化速度轨迹。 然后获得了所有十个效率组上相应的能耗相对变化,并且针对不同道路地形的统计数据如图7所示。图7(a)显示SOC值略低于具有不同道路地形的SOC值。 每次比较的精确效率,3σ 变化均在 0.1% 以内。 图7(b)显示了与使用精确效率值的结果类似的比较结果,并且3σ变化均在0.2%以内,这表明ADMM控制器对不确定的车辆参数具有较高的鲁棒性。 ADMM 控制器的鲁棒性验证了第二节中导出的用于速度优化目的的卡车能耗模型的有效性。

5)不同预测范围下的性能:在实践中,预测范围可以根据交通、道路地形、计算要求等而变化。 一般来说,预测范围越长,从未来获得的信息越多,计算负担也越重。 图8给出了基于不同前视视野的控制结果。 H后面的数字表示分段数N。例如,H20表示N为20,因此预测范围为1000m。 在每个预测范围内,将基于 ADMM 的控制器的 SOC 降低与基于 CC 的控制器进行比较,然后推导 SOC 的相对变化并如图 8 所示。图 8 表明,能耗普遍下降 ,而计算时间随着视野的增加而增加。 H30后,SOC(绝对值)的相对变化在图8(a)中略有下降,在图8(b)中缓慢增加。 此外,H30 处的计算时间均小于 1.2 秒,低于本例中实时操作的最大周转时间 2 秒。 因此,在仿真中将段数设置为30是合理的。
请注意,如果未来道路地形或交通不确定,则可以减小预测范围以提高未来信息的预测置信度。 在本研究中,假设提前知道交通和道路地形的确切信息。
B. Optimal Speed Control Under Traffic
如前所述,周围流量可以轻松引入优化 PMEP^{ME}PME。 附录C给出了车辆以安全、节能的方式行驶的详细建模过程,具体来说,速度上限 xi‾\overline{x_i}xi 适应于前车的速度。
1)交通随机建模:需要模拟卡车周围的交通,以实现基于交通的最优速度控制。 这里,指数分布用于生成随机流量。 指数分布是一种标准分布,可以对车辆之间的到达间隔进行建模[29]。 设事件“1”和“0”分别表示是否有前车。 如果使用指数分布来表示事件“1”和“0”之间经过的时间,则流量是马尔可夫过程[30]。 如果连续随机变量 X 具有概率密度函数,则称其具有指数分布
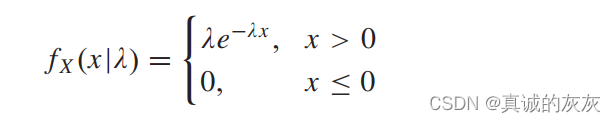
其中 λ>0λ > 0λ>0 称为分布率。 这里,XXX 代表行进距离而不是持续时间,因为在这种情况下距离和持续时间总是可以相互转换的。 用 X1X_1X1 表示有前车的行驶距离,用 X2X_2X2 表示无前车的行驶距离,则这两个分布的平均值为 μ1=1/λ1μ_1=1/λ_1μ1=1/λ1 和μ2=1/λ2μ_2=1/λ_2μ2=1/λ2。 交通状况由 μ1和μ2μ_1和μ_2μ1和μ2 的值决定。 大的 μ1μ_1μ1 和小的 μ2μ_2μ2 表示交通流量大,反之亦然。 μ1和μ2μ_1和μ_2μ1和μ2 可以根据可用的真实交通流数据进行校准。
2)模型初始化:为了定义流量特征,需要初始化一些模型参数。 在本研究中,自动跟随卡车与前车的最小车头时距 hτh_{\tau}hτ 设置为 1.2s,以确保交通安全[31]。 假设与前车的初始距离 did_idi 在[2, 4] s 车头时距范围内均匀分布,前车速度 vpv_pvp 假设在[70, 80] km/h 范围内均匀分布。 交通繁忙的特征为 (μ1=3,μ2=2)(μ_1 = 3 ,μ_2 = 2)(μ1=3,μ2=2)。 轻量交通的特征为(μ1=2,μ2=3)(μ_1 = 2,μ_2 = 3)(μ1=2,μ2=3),正常交通的特征为(μ1=3,μ2=3)(μ_1 = 3,μ_2 = 3)(μ1=3,μ2=3)。 请注意,在这种情况下,行程时间 τ\tauτ 高度依赖于交通状况,因此无法提前确定。
3)涉及交通的速度控制结果:在本节中,我们首先研究了平坦道路(道路坡度= 0)上跟随前车的卡车的能耗结果。 然后,我们进一步研究了卡车在不同坡度道路上跟随前车的能耗。 最后,分别根据交通拥挤和交通稀疏的情况对从南泰利耶到北雪平的卡车能耗结果和返回进行了评估。 在涉及周边交通的场景中,由于无法引入基于DP或PIC的速度轨迹进行比较,因此仅使用基于CC的速度轨迹作为基准。
图9所示为平坦道路上不同前车速度和初始距离的仿真结果。 请注意,CC 速度是根据两个规则获得的:首先,CC 行驶时间与基于 ADMM 的相同,其次,CC 车头时距也设置为 1.2 s。 据观察,在这两种情况下,ADMM 控制器比 CC 节省更多能量,因为 ADMM 控制器在平坦道路上制动较少。 在情况1中,ADMM使用阻力(空气和摩擦)来减速,而CC使用额外的制动,从而消耗更多的能量。 在情况2中,ADMM控制器首先制动一段时间,然后根据阻力完美减速,而CC控制器则制动直至达到所需速度。 图9显示,我们的方法仍然致力于为跟随前车的卡车节省能量,并且随着道路坡度的增加,预计会进一步节省更多的能量。
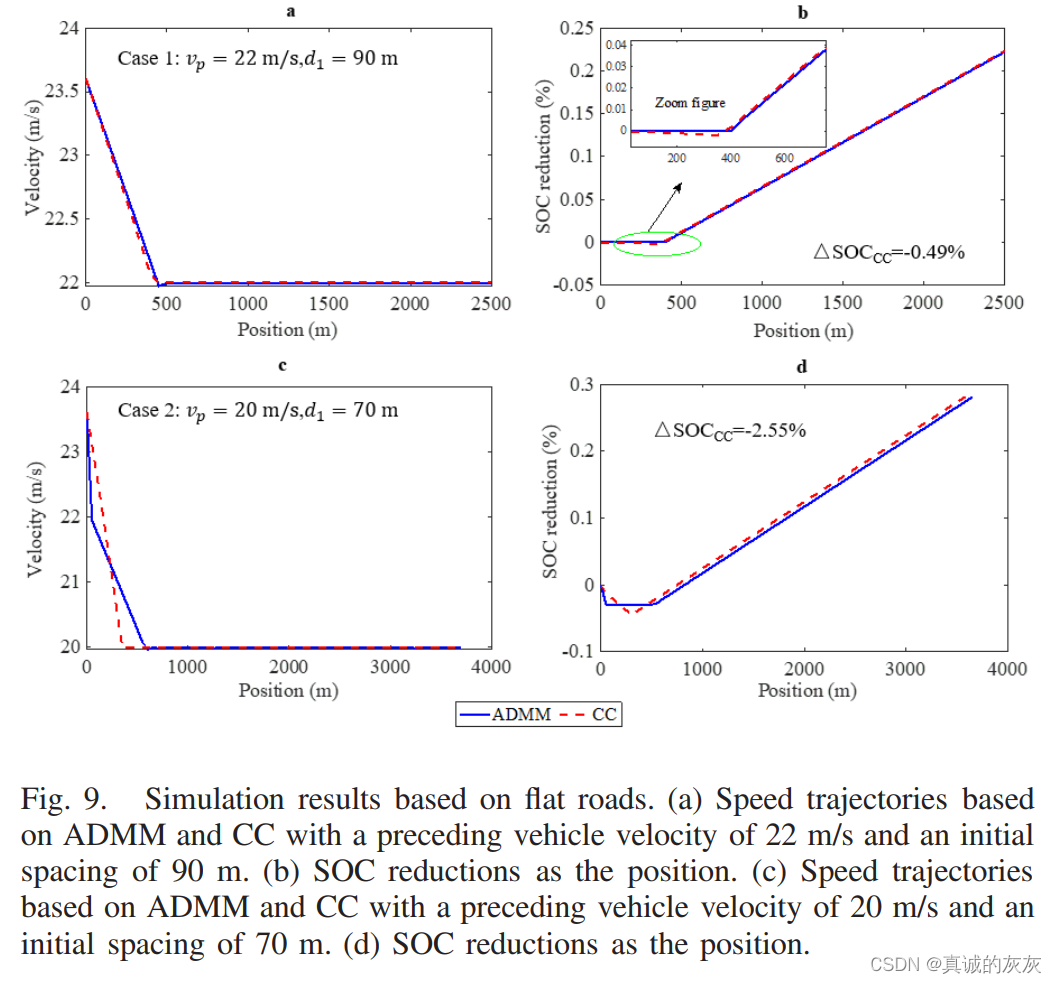
图 10 显示了图 5 中道路坡度的模拟结果。据观察,ADMM 的制动次数仍然更少,并且更节能。 图10(b)和(d)显示,与基于CC的能耗相比,基于ADMM的能耗分别降低了6.07%和19.46%。 这些结果表明,我们的方法在改善卡车在不同坡度的道路上跟随前车的能耗方面仍然表现出色。
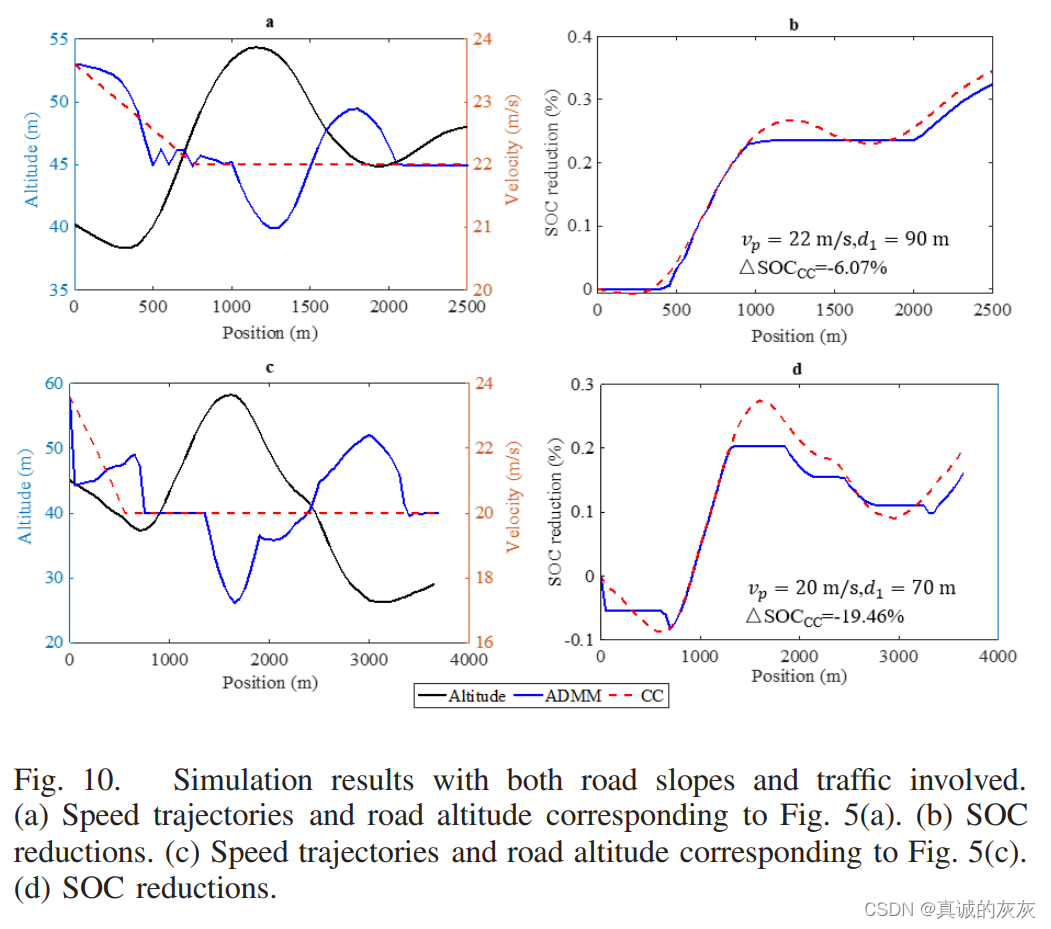
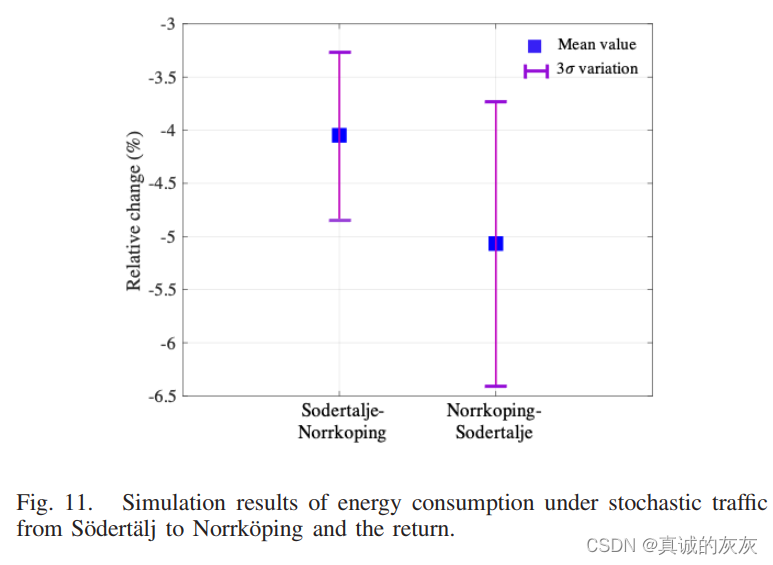
图 11 显示了从 Södertälj 到 Norrköping 以及返回的随机流量下的统计结果。 对于每个方向,随机生成十种交通场景,涵盖交通拥堵(μ1=3和μ2=2)(μ_1 = 3 和 μ_2 = 2)(μ1=3和μ2=2)、交通畅通(μ1=2和μ2=3)(μ_1 = 2 和 μ_2 = 3)(μ1=2和μ2=3)和交通正常(μ1=3和μ2=3)(μ_1 = 3 和 μ_2 = 3)(μ1=3和μ2=3),并实施以验证 ADMM 的性能。
对于每种交通场景,前车随机进出,有前车(标记为“交通”)和无任何前车(标记为“无交通”)的总行驶里程列于表3。 从南泰利到北雪平,场景1-3表示拥堵,场景4-7表示拥堵,场景8-10表示正常拥堵。 对于回程方向,场景1-4为大流量,场景5-7为小流量,场景8-10为正常流量。

在每种交通场景下,计算ADMM和CC之间能耗的相对变化,并通过总结不同交通场景下的仿真结果进一步获得平均值和3σ变化。 据观察,从南雪平到北雪平,ADMM 的能耗比基于 CC 的能耗降低了 4.05%,3σ 区间为 [3.27%, 4.83%],而从北雪平到南雪平,节省的能源高达 5.07%,3σ 区间为 [3.73%, 6.40%]。 这些节能结果表明,我们的方法可以很好地适应不同的交通情况,以实现最低能耗的目的。
V. EVALUATION OF BATTERY AGING UNDER ECO-DRIVING 经济驾驶下电池老化评估
能量最小化只是电池电动重卡经济驾驶控制的问题之一。 驾驶算法对电池健康状况的影响也与此相关。 受限于目前的电池技术,电池寿命普遍比EV寿命短[32],而电池电动重卡由于长途行驶的要求,电池寿命更短。 因此,电池电动重卡中的电池老化不仅需要在线监测,还需要进一步改进。
事实上,近年来针对电池 SOH 估算进行了许多研究,例如 Chen 等人。 [33]开发了一种利用双H无穷大滤波器实时估计电池SOH的有前途的方法,并且通过硬件在环实验验证了高估计精度,而关于管理EV实时操作以延长电池寿命。 这里证明了所提出的方法对电池老化的积极影响。
A. EV Battery Life Model
电池老化包括循环老化和日历老化[34]-[36]。 对于长途电动重卡,一种合适的运营模式是白天运输,晚上充电。 这种操作模式表明卡车电池组将在一天中的大部分时间进行循环。 在这种情况下,只需评估BE HDT电池的循环老化即可。
本文使用的电池循环老化模型是在[36]中开发的。 选择该模型有两个原因。 该模型首先分析了再生制动对电池老化的影响,并将这种影响纳入老化模型中。 其次,模型通过大量模拟电动汽车运行的实验数据进行验证。 恒定温度下的总容量衰减表示为
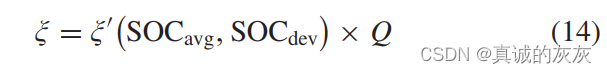
其中,ξ\xiξ 是总容量衰减, QQQ 是充电/放电过程中的安时 (Ah) 电荷, ξ′\xi 'ξ′是容量衰减率,单位是电池每充放 1Ah 时衰减的 Ah 数。 容量衰减率表示为
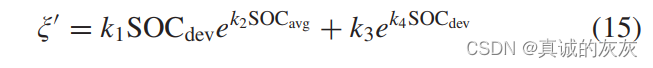
其中 k1–k4k_1–k_4k1–k4 是四个模型拟合参数。 SOCavg=(1/(Qt1−t0))∫Qt0Qt1SOC(Q)dQSOC_{avg} = (1/(Q_{t1−t0})) \int_{Q_{t0}}^{Q_{t1}} SOC(Q) dQSOCavg=(1/(Qt1−t0))∫Qt0Qt1SOC(Q)dQ 表示平均 SOC,Qt0Q_{t0}Qt0 为 t0t_0t0 时刻充放电的电量,Qt1Q_{t1}Qt1 为 t1t_1t1 时刻充放电的电量, Qt1−t0=Qt1−Qt0Q_{t1−t0} = Q_{t1} − Q_{t0}Qt1−t0=Qt1−Qt0。 SOCdev=((1/(Qt1−Qt0))∫Qt0Qt1(SOC(Q)−SOCavg)2dQ)1/2SOC_{dev} = ((1/(Q_{t1} − Q_{t0})) \int_{Q_{t0}}^{Q_{t1}} (SOC(Q) − SOC_{avg})^2 dQ)^{1/2}SOCdev=((1/(Qt1−Qt0))∫Qt0Qt1(SOC(Q)−SOCavg)2dQ)1/2 表示 SOC 平均值的归一化标准偏差。 假设车辆的热管理系统能够将电池组保持在25℃的恒定温度,模型参数 k1–k4k_1–k_4k1–k4 因此在此特定温度下初始化[36]。
SOCavgSOC_{avg}SOCavg和SOCdevSOC_{dev}SOCdev不太明白是什么意思。。。平均SOC是说一次跑长途的平均SOC吗,SOC平均值的归一化标准偏差是什么意思,一次跑长途的SOC的标准差吗???不太明确是一次跑长途还是一段时间的多次跑长途的数据
从容量衰减率上看,平均SOC越大,容量衰减越快,SOC使用的范围越大,容量衰减越快,这个倒是好理解,充满电后使用时剩余的SOC越小对电池伤害越大
启示:尽量减少电池充放电容量到达两个极端,尽量不要充满和尽量不要放完
B. Optimal Speed Control Impact on Battery Aging
1)仿真参数预设:电池老化模型表明,一般情况下,在SOC平均值较低的SOC循环范围内,电池寿命较长。 因此,为了公平比较,每个控制器将结束时的 SOC 而不是初始的 SOC 调整为相同值。 一般来说,长途重卡每个工作日的行驶里程应在500公里以上。 因此,重复从 Södertälj 到 Norrköping 以及返回(约 240 公里长)的道路数据,以生成具有所需行驶距离的道路数据剖面。 假设卡车白天运货,晚上充电。 为了延长电池寿命,慢速充电是首选,因此,模拟中充电速率设置为0.1C。 请注意,预计卡车每个工作日都会使用,因此每年将运行 260 天。 目前,电动汽车电池的退化极限被约定为30%[32]。
2)不涉及交通的电池老化:这里模拟了三种情况,每种情况下,卡车每天行驶预定的距离或电池组达到预定的结束SOC。
案例1:卡车每天行驶800公里,这是特斯拉声称的卡车电池充满电的行驶里程。 对于全新电池组,ADMM 和 CC 基准的电池(放电深度)DOD 在行程结束时分别为 90.86% 和 95.12%,一个电池组的 Ah 充放量分别为 328.8 Ah 和 400.3 Ah 。 据观察,使用 ADMM 进行速度控制后,电池提供的电量减少了 71.5 Ah,占电池标称容量(312.5 Ah)的 22.9%。 由于容量衰减与 Ah 吞吐量成正比(参见电池老化模型),因此与 CC 策略相比,ADMM 控制器预计可将电池老化降低 20% 以上。 这一显着改进表明,与 CC 策略相比,所提出的经济控制算法不仅最大限度地减少了能耗,而且还延长了电池寿命。
电池健康状况的改善来自于所提出的最小能量控制避免了不良制动的事实。 请注意,与避免不良制动的情况相比,每次不良制动时电池释放的再生电量大约是两倍。
在这种情况下,ADMM 和 CC 基准的 SOC 循环范围分别为 [95.74%, 4.88%] 和 [100%, 4.88%]。 电池老化评价结果如表IV所示。 令人惊讶地发现,基于ADMM的电池的一年容量衰减 ξ\xiξ 比CC降低了35.2%。 ADMM 控制器导致电池 DOD 较低,因此 SOCavgSOC_{avg}SOCavg 和 SOCdevSOC_{dev}SOCdev 比 CC 控制器更小。 与使用 CC 相比,这种低电池 DOD 导致使用 ADMM 的容量衰减率 δξ\delta \xiδξ 降低了 15.5%,这解释了为什么 ADMM 降低电池容量衰减的程度远高于上述值 20%。
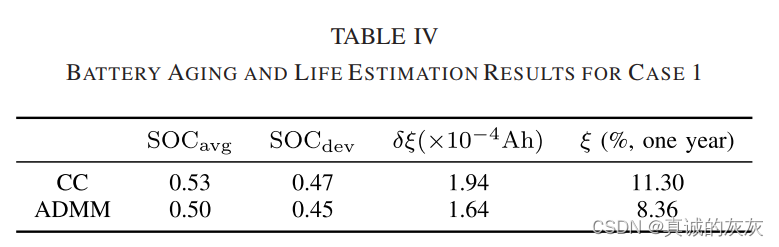
案例2和案例3:一般情况下,电动汽车在电池SOC低于10%~20%时需要充电。 因此,在案例 2 和案例 3 中,CC 的电池终止 SOC 分别设置为 10% 和 20%,这对应于基于 CC 的卡车每天更换新电池的行驶距离为 761 公里和 675 公里。 为了公平比较,基于ADMM的续驶里程被设置为与基于CC的相同值。图12和13分别显示了情况2和3的电池老化结果,其中还给出了相应DOD内基于CC的行驶里程。 据观察,随着电池容量的降低,行驶里程会减少。 在案例 2(图 12)中,基于 CC 和 ADMM 的电池寿命分别为 3.74 年和 7.81 年,表明 ADMM 的寿命延长了 108.8%。 在 CC 的电池寿命终止 (EOL) 时,卡车的续驶里程减少至约 517 公里,相当于与初始续驶里程相比,里程缩水了 32%。
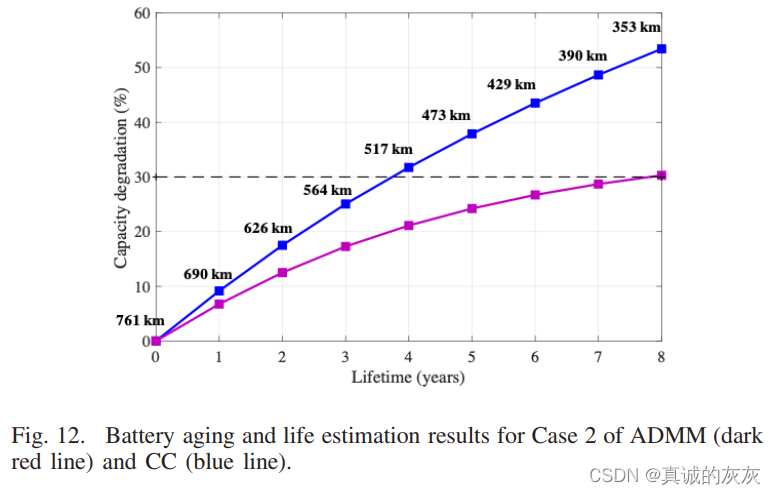
在案例3(图13)中,由于电池DOD比案例2短10%,因此基于CC和ADMM的电池寿命都更长,分别约为6年和10.5年,表明寿命 ADMM 延长 75%。 在这种情况下,续驶里程减少了202公里,相当于续航里程缩水了43%,这表明从电动汽车行驶的角度来看有必要减少电池老化。
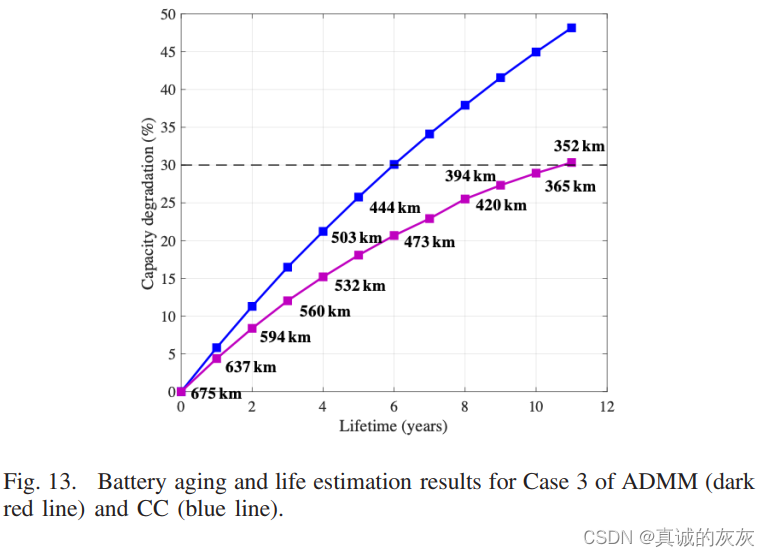
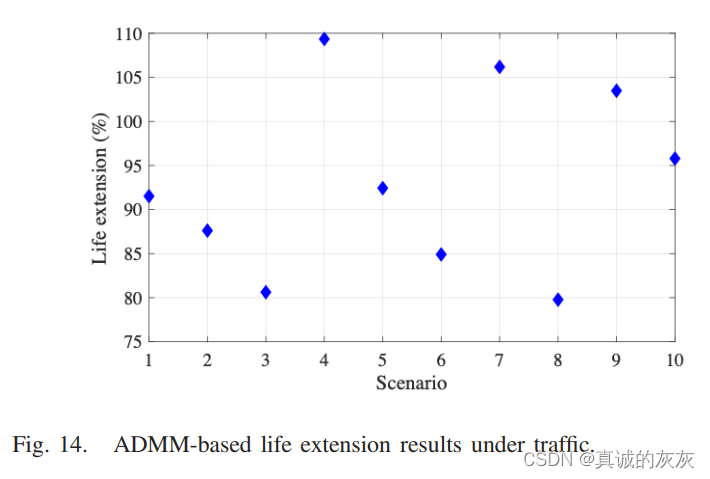
3) 交通状况下的电池老化:在本例中,使用了交通状况下的最佳速度曲线,并且如前所述,生成的从南泰利耶到北雪平和回程的随机交通场景涵盖了拥堵交通、通畅交通和正常交通。 对于每个场景,从南泰利到北雪平以及返程的道路海拔和交通情况都被连接并重复,以生成所需的道路剖面进行模拟,从而形成了总共十种不同交通情况下的模拟情况。 图 14 显示了这 10 种交通场景下基于 ADMM 的寿命延长结果与 CC 的比较,其中基于 CC 的每天结束的SOC 在不同的老化阶段被设置为 15%。 基于ADMM的每日驾驶范围也设置为与基于CC的相同值,以进行公平比较。 据观察,基于 ADMM 的寿命延长范围为 80% 至 110%,平均值高达 93.2%。
VI. CONCLUSION
本文开发了一种以最小能耗和延长电池寿命控制卡车速度的方法。 构建创新的状态空间方程来描述卡车的系统动力学。 卡车运行速度和能耗消耗由状态空间模型获得,其中卡车速度作为状态,电池 SOC 作为输出。 定义了能量最小化问题,引入了一种基于 ADMM 原理的新型优化技术来获得最佳解决方案,并结合 MPC 策略来处理即将到来的道路地形和交通的不确定性,从而实时规划卡车速度。 基于瑞典南泰利市和北雪平市之间的真实高速公路海拔高度验证了所开发方法的性能。
仿真结果表明,所开发的方法能够利用地形条件来改善能源管理,无论是在最大限度地减少电池总放电量还是延长电池寿命方面。 结果表明,ADMM控制在不同场景下比DP控制、PIC和匀速CC消耗更少的能量。 一般来说,ADMM 比 CC 消耗的能量少 4%–5%。 令人惊讶的是,ADMM 通常比 CC 延长电池寿命 1 倍以上。 这些结果表明有必要通过优化卡车速度轨迹来改善电池能耗和老化。 当引入交通流时,电池能量和老化改善值仍然成立,这表明我们的方法也可以用于城市驾驶的电动公交车和乘用电动汽车。
APPENDIX A :EM MODELING 电动机建模
假设电动机在牵引和再生制动模式下具有相似的效率。 电动机功率 PEMP^{EM}PEM 表示为
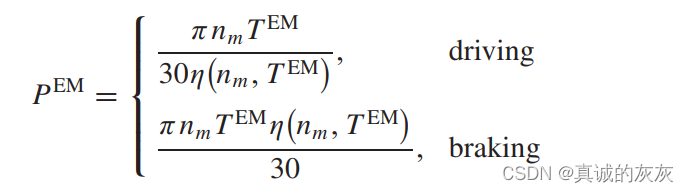
其中 TEMT^{EM}TEM 表示电动机扭矩,nmn_mnm 表示电动机的转速,η(nm,TEM)η(n_m,T^{EM})η(nm,TEM) 表示取决于 nmn_mnm 和 TEMT^{EM}TEM 的电机效率。 Tesla Semi 的电磁效率图如图 15 所示 [37]
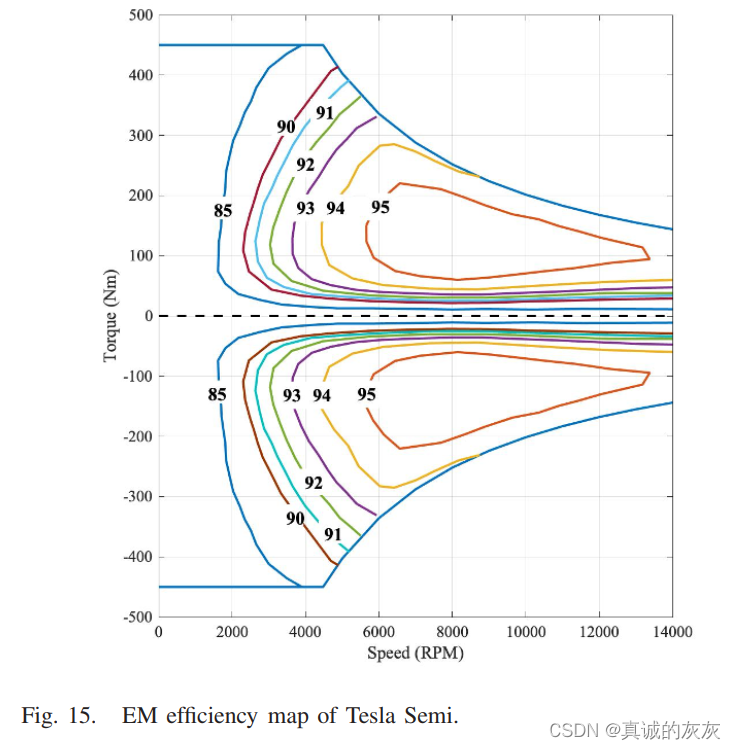
备注:据称 Tesla Semi 与其 Model 3 共享许多部件,包括相同的电机 [38](图 15)。
车辆速度 vvv 和电动机转速 nmn_mnm 由下式联系:

其中 igi_gig 表示齿轮比,rwhlr_{whl}rwhl 表示车轮半径。 请注意,高速公路上的卡车速度限制在 [75, 90] km/h 范围内 [11]。 在这种情况下,在齿轮比为19:1时,电动机的转速范围在[7000, 9000] r/min内[39]。 在此转速范围内,电动机 以高效模式运行,效率约为 94%。 因此,在计算动力系统效率 βiβ_iβi 时,电动机效率也可以被认为是一个常数。
APPENDIX B:OUTPUT FUNCTION MODELING 输出函数建模
这里考虑四种情况。
情况一:在第 i 段内,Fitrack(t)>0F_i^{track}(t) > 0Fitrack(t)>0,即电池始终放电。 注意,由于式(3)中的1/UC是一个常数,为了简洁起见,在下面的推导中将其暂时删除,但在仿真结果中将被重新添加:
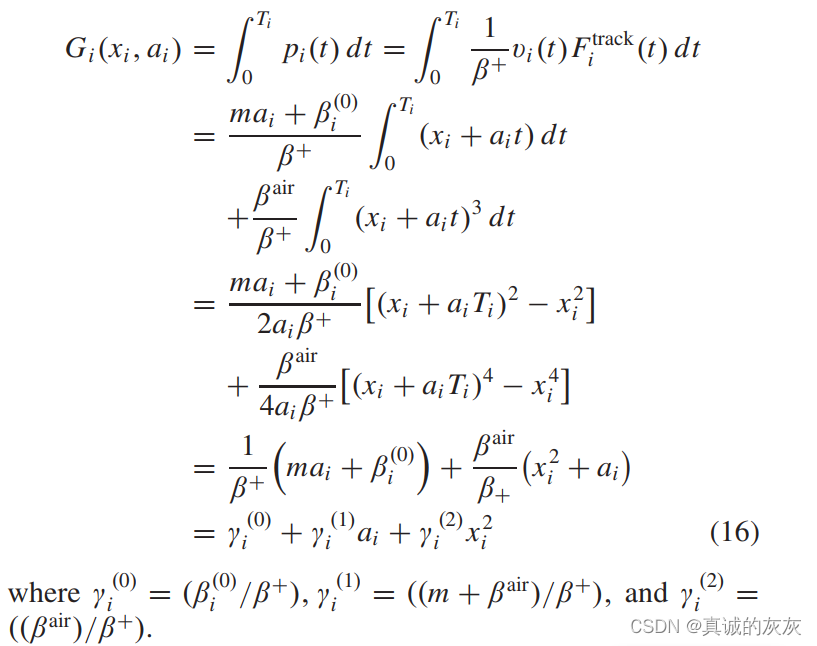
推导备注:s=v0∗t+1/2∗a0∗t2s=v_0*t+1/2*a_0*t^2s=v0∗t+1/2∗a0∗t2,这里令s=1?,所以推出来的(xi+aiTi)2−xi22ai=Tixi+aiTi22=1?\frac{(x_i+a_iT_i)^2-x_i^2}{2a_i}=T_ix_i+\frac{a_iT_i^2}{2}=1?2ai(xi+aiTi)2−xi2=Tixi+2aiTi2=1?
推导备注:(xi+aiTi)2+xi2=2xi2+2ai==>(xi+aiTi)2−xi22ai(x_i+a_iT_i)^2+x_i^2=2x_i^2+2a_i==>\frac{(x_i+a_iT_i)^2-x_i^2}{2a_i}(xi+aiTi)2+xi2=2xi2+2ai==>2ai(xi+aiTi)2−xi2
根据这两个备注就能推出来上面的推导结果
情况二:第 i 段内 Fitrack(t)<0F_i^{track}(t) < 0Fitrack(t)<0,即电池一直在充电。 适用案例 I 的推导。 将 β+ 替换为 β−,有
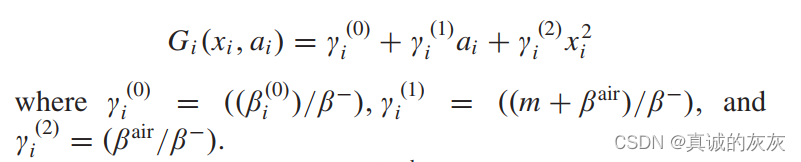
情况三:FitrackF_i^{track}Fitrack 的符号由正变为负,即存在 ti∗t_i^*ti∗ 使得
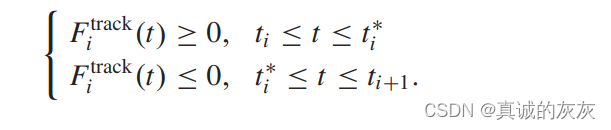
请注意,ti∗t_i^*ti∗ 是 (xi,ai)(x_i, a_i)(xi,ai) 的函数。 这种情况的原理图如图16所示。

输出函数是两个子段的和

遵循下面的状态转移函数(2):
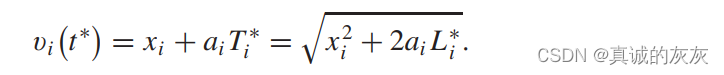
将上式代入(17)式有
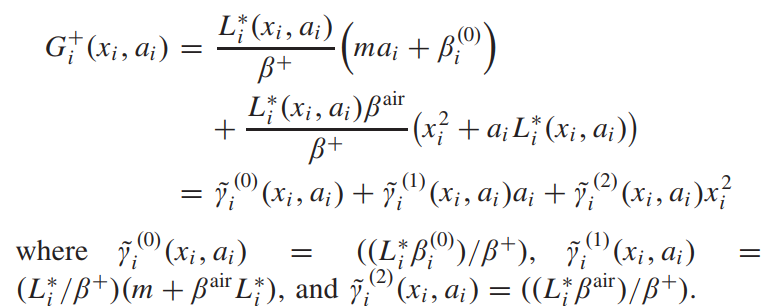
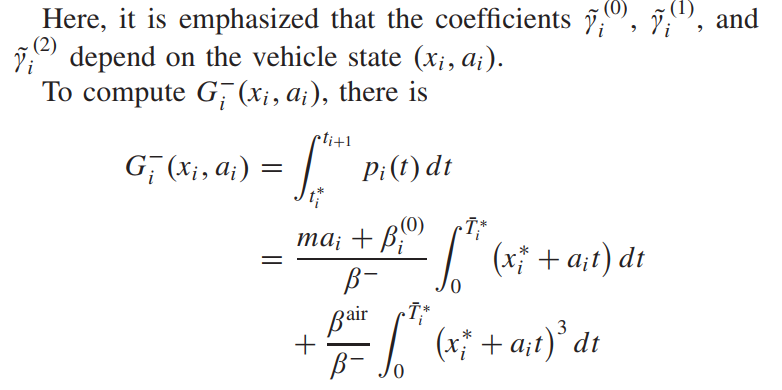
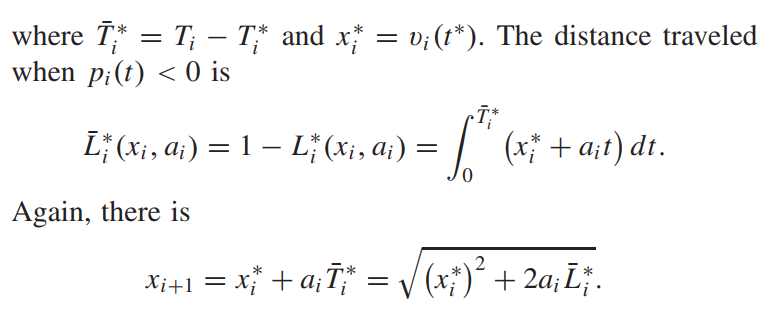
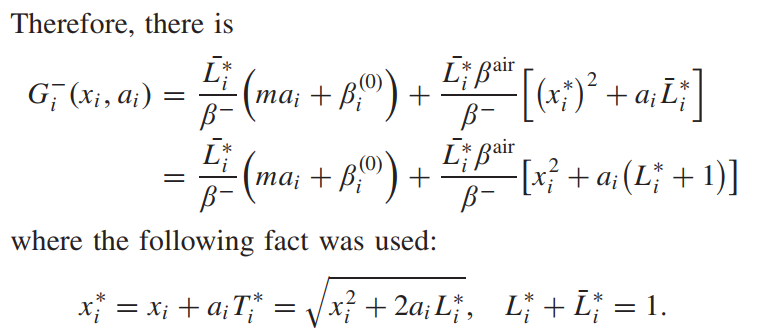
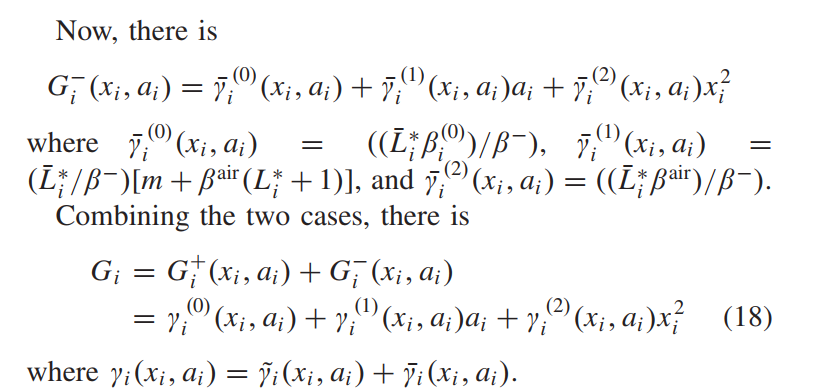
情况四:FitrackF_i^{track}Fitrack 的符号由负变正,即存在 ti∗t_i^*ti∗ 使得
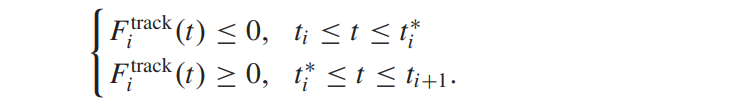
这种情况下的推导与情况 III 中的相同,因此与 (18) 共享相同的 Gi(xi,ai)G_i(x_i, a_i)Gi(xi,ai) 表达式,但 γi(0)、γi(1)和γi(2)γ_i^{(0)}、γ_i^{(1)} 和 γ_i^{(2)}γi(0)、γi(1)和γi(2) 的值不同 )。
因此,第 i 段驱动力的符号由向量 (xi,ai)(x_i,a_i)(xi,ai) 决定,不同情况下向量参数 γiγ_iγi 的表达式如**表V **所示。
APPENDIX C:DERIVATION OF UPPER SPEED LIMIT 速度上限的推导
卡车与前车之间必须始终保持安全车距,以保证行驶安全,即根据前车速度限制卡车在下一段的最大允许速度。 车头时距定义为前车与后车到达指定测试点之间所经过的时间。 让我们用 hτh_τhτ 来表示车头时距,因此有

其中 ddd 是两辆车之间的间距,vfv_fvf 是后面车辆的速度。 为保证卡车通过 i 路段的行驶安全,有
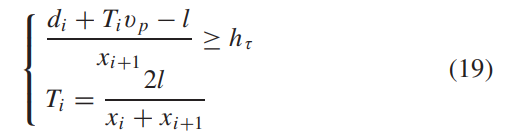
其中,did_idi 是路段 i 起点处与前车的间距,lll 是每个路段的参数化长度,vpv_pvp 是前车的速度,并假设为常数。 根据(19)式,有
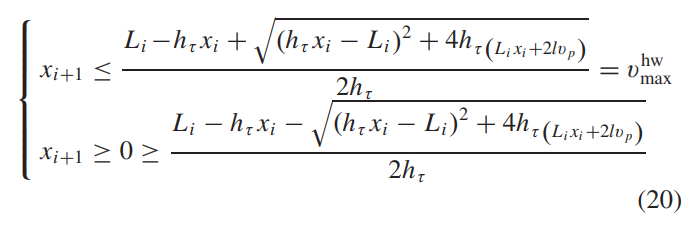
其中 Li=di−l,i=1,2,...,NL_i = d_i − l, i = 1, 2, ...,NLi=di−l,i=1,2,...,N。因此,优化时 xi+1x_{i+1}xi+1 的最大允许值为 xi+1‾=min(vmax,vmaxhw\overline{x_{i+1}} = min(v_{max}, v_{max}^{hw}xi+1=min(vmax,vmaxhw ),其中vmaxv_{max}vmax是欧盟法律上允许的最大速度。
(19)推导备注:di为i时刻两车之间的距离,则第i+1时刻两车的距离di+1=前车的位置−自车的位置=(di+Tivp)−(xi+xi+12∗Ti),由于Ti=2lxi+xi+1,则di+1=di+Tivp−l>=xi+1hτ,则推出di+Tivp−lxi+1>=hτd_i为i时刻两车之间的距离,则第i+1时刻两车的距离d_{i+1}=前车的位置-自车的位置=(d_i+T_iv_p)-(\frac{x_i+x_{i+1}}{2}*T_i),由于T_i=\frac{2l}{x_i+x_{i+1}},则d_{i+1}=d_i+T_iv_p-l>=x_{i+1}h_{\tau},则推出\frac{d_i+T_iv_p-l}{x_{i+1}}>=h_{\tau}di为i时刻两车之间的距离,则第i+1时刻两车的距离di+1=前车的位置−自车的位置=(di+Tivp)−(2xi+xi+1∗Ti),由于Ti=xi+xi+12l,则di+1=di+Tivp−l>=xi+1hτ,则推出xi+1di+Tivp−l>=hτ
(20)推导备注:
di+Tivp−lxi+1>=hτ令Li=di−l,i=1,2,...,NLi+Tivpxi+1>=hτLi+Tivp>=hτxi+1Li+2lxi+xi+1vp>=hτxi+1Lixi+Lixi+1+2lvp>=hτxi+12+hτxixi+1hτxi+12+(hτxi−Li)xi+1−(Lixi+2lvp)<=0 \frac{d_i+T_iv_p-l}{x_{i+1}}>=h_{\tau} \\ 令 L_i = d_i − l, i = 1, 2, ...,N \\ \frac{L_i+T_iv_p}{x_{i+1}}>=h_{\tau} \\ L_i+T_iv_p>=h_{\tau}x_{i+1} \\ L_i+\frac{2l}{x_i+x_{i+1}}v_p>=h_{\tau}x_{i+1} \\ L_ix_i+L_ix_{i+1}+2lv_p>=h_{\tau}x_{i+1}^2+h_{\tau}x_ix_{i+1} \\ h_{\tau}x_{i+1}^2+(h_{\tau}x_i-L_i)x_{i+1}-(L_ix_i+2lv_p)<=0 \\ xi+1di+Tivp−l>=hτ令Li=di−l,i=1,2,...,Nxi+1Li+Tivp>=hτLi+Tivp>=hτxi+1Li+xi+xi+12lvp>=hτxi+1Lixi+Lixi+1+2lvp>=hτxi+12+hτxixi+1hτxi+12+(hτxi−Li)xi+1−(Lixi+2lvp)<=0
通过一元二次方程的求解方法就可以得到该解,通过调整 lll 就可以调整跟随跟车时距的快慢了
ACKNOWLEDGMENT
作者要感谢福特汽车公司的 Hellström 博士分享瑞典南泰利市和诺尔雪平市之间的道路海拔数据,并与 Scania AB 的工程师进行了广泛的讨论。
























 905
905

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








