数据结构与算法-树

一、树的定义

由 n(n>=0)个数据节点组成的集合，有n个元素和n-1条边(Edge)，n>0时，有一个根节点(root)和n-1个子节点(child)。

特性：

可以是空树；

n>1时，其余节点又可分为多个子集，每个子集又是一棵树，位于根节点(父节点(parent))左边的是他的左子树，右边的是它的右子树；

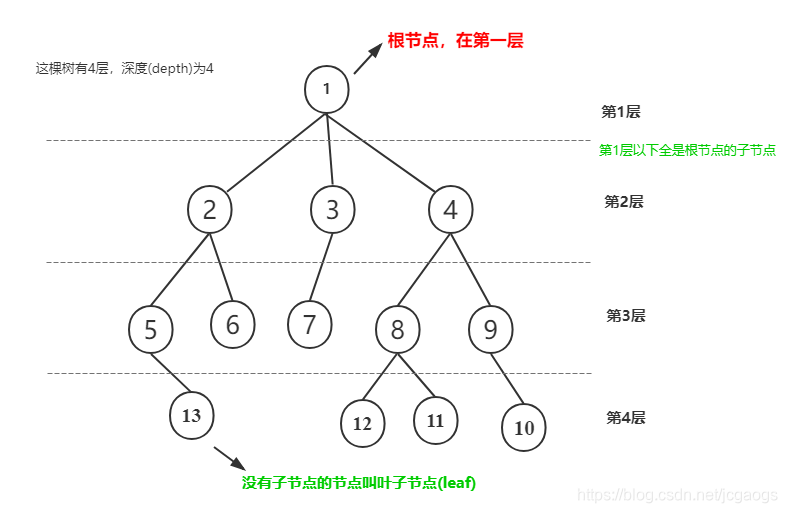
如下图，树的数据可以有多层，这叫树的深度 depth，从根开始是第1层；

没有子节点的节点，被称为叶子节点（leaf）；

二、二叉树

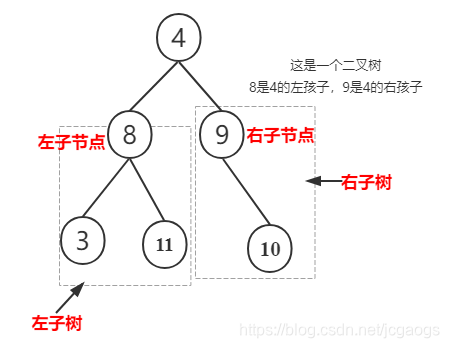
在树的基础上，每个节点的子节点限定不超过2个，也可以是空树

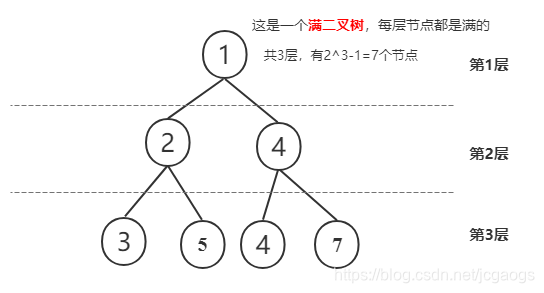
高度为n，并且总共有2^n -1个节点的是 满二叉树，即每个节点都达到最大数，都是满的。

在二叉树中，最底层从最右边起去掉相邻的若干叶子节点，得到的二叉树，就是完全二叉树

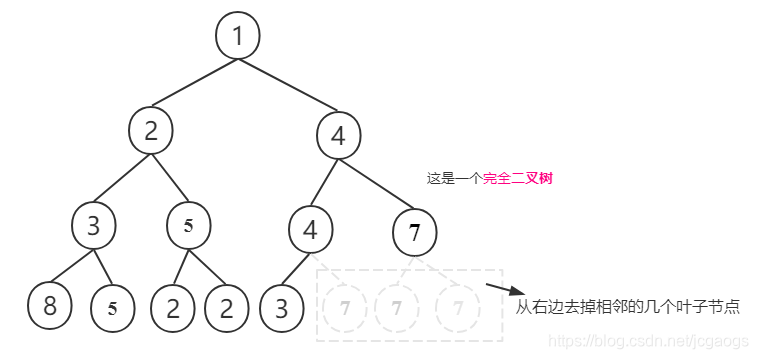
满二叉树必定是完全二叉树，反正完全二叉树不一定是满二叉树。

特性：

1.二叉树的第n层，最多有2^(n-1)个节点,(n从1开始)；

2.深度(depth)为n的二叉树最多有2^n-1个节点；

3.二叉树，如果其叶子节点数为k1个，有2个子节点的节点有k2个，那么一定满足 k1=k2+1；

4.包含n个结点的二叉树的高度至少为log2 (n+1)；

 

---

二叉树的存储结构 

顺序存储和链式存储结构，实际开发中链式用的多。

1.首先，顺序存储：是用一组连续的存储单元存放二叉树的所有结点，依据二叉树的性质，完全二叉树和满二叉树采用顺序存储比较合适，把二叉树节点编号和数组下标对应起来，结点的序号可以唯一地反映出结点之间的逻辑关系，这样能够最大可能地节省存储空间。

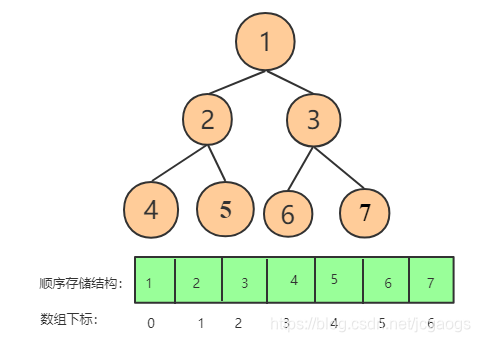
但是一般普通的二叉树，要采用数组结构存储，只能在其空余位置补充null节点，这样才能当做是完全二叉树，这会导致存储空间的浪费：

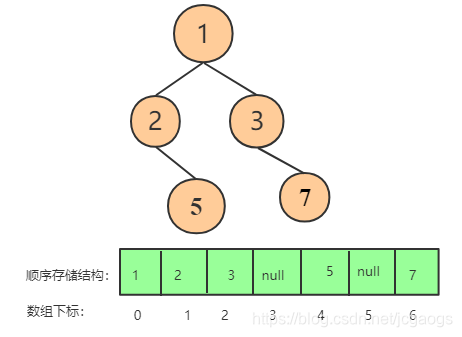
1.因此，推荐使用链式存储：每一个结点包含三个关键属性:指向左子树的指针，节点数据，指向右子树的指针；

根据这个，链式存储结构如下：

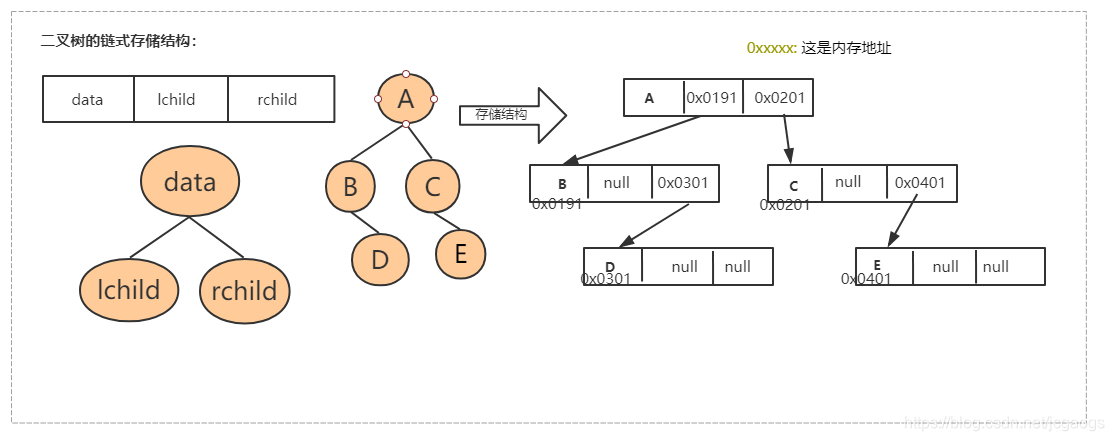
 为了方便访问结点的父节点(parent)，还可以给链表结点增加一个字段parent,用来指向父亲结点。这样每个结点由四个属性组成，结构就变成这样了：

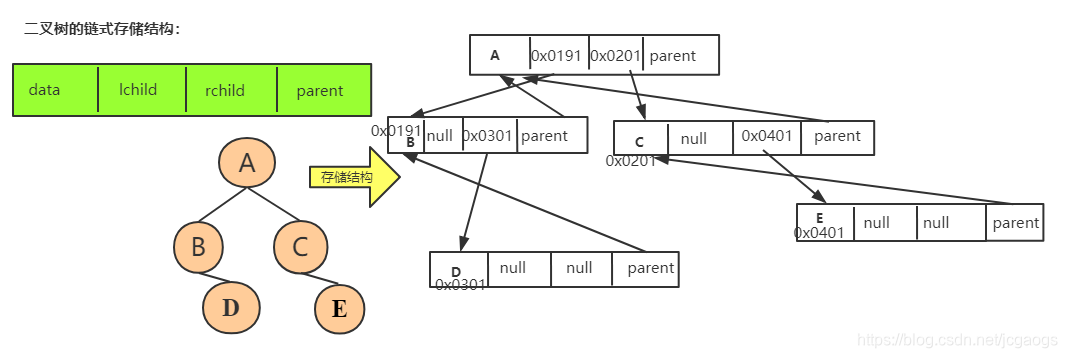
这样的结构表示的二叉树的链式存储结构，称为三叉链表。

---

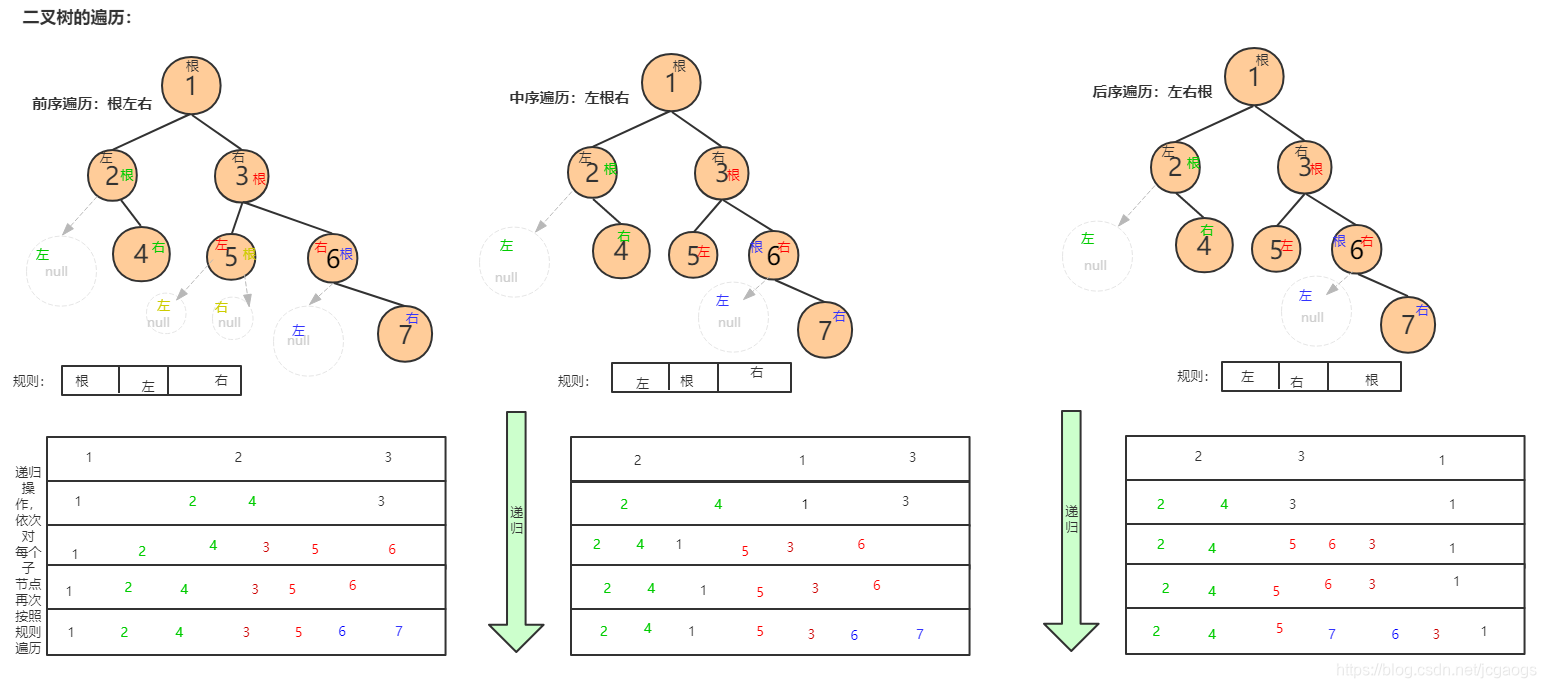
二叉树的遍历

分为3种顺序的遍历，分别是前序、中序、和后序遍历，如下图：

遍历步骤图解：