WTF！他们说的主成分分析（PCA）是怎么回事

1 PCA目的/作用

PCA是最常用的线性降维，不知道大家有没有了解过latent space，也就是隐空间，也是一种降维的方式。PCA是用线性投影，将高维投到低维。

且目标是：所投影的纬度上信息量最大（方差最大），且即为最不相近。较少纬度，保留最大的特性。在信息量不丢失，不损耗（尽量）

   2 求解步骤

1.去除平均值
2.计算协方差矩阵
3.计算协方差矩阵的特征值和特征向量
4.将特征值排序
5.保留前N个最大的特征值对应的特征向量
6.将原始特征转换到上面得到的N个特征向量构建的新空间中（最后两步，实现了特征压缩）
 

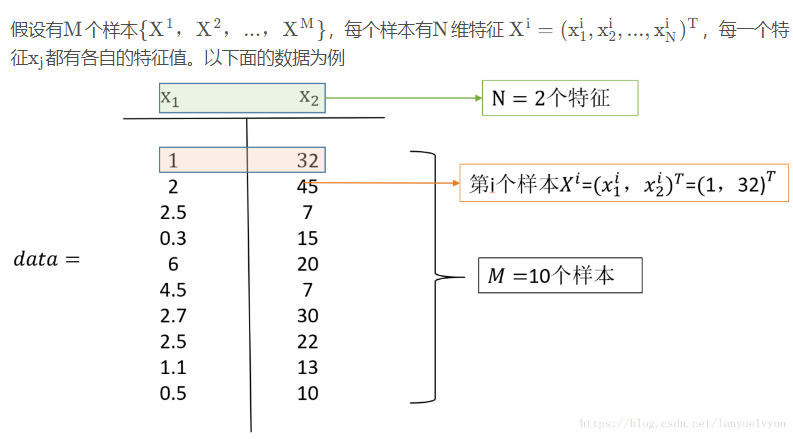
 第一步：对所有特征进行中心化：去均值（really important）

求每一个特征的平均值，然后对于所有的样本，每一个特征都减去自身的均值。

 第二步：求协方差矩阵C

 

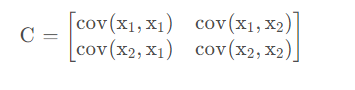
 第三步：求协方差矩阵C的特征值和相对应的特征向量

利用矩阵的知识，求协方差矩阵 C 的特征值λ 和相对应的特征向量 u（每一个特征值对应一个特征向量）：

Cu=λu

第四步：将原始特征投影到选取的特征向量上，得到降维后的新K维特征

4 PCA优缺点
优点：
1、以方差衡量信息的无监督学习，不受样本标签限制。
2、由于协方差矩阵对称，因此k个特征向量之间两两正交，也就是各主成分之间正交，正交就肯定线性不相关，可消除原始数据成分间的相互影响
3. 可减少指标选择的工作量
4.用少数指标代替多数指标，利用PCA降维是最常用的算法
5. 计算方法简单，易于在计算机上实现。
缺点：
1、主成分解释其含义往往具有一定的模糊性，不如原始样本完整
2、贡献率小的主成分往往可能含有对样本差异的重要信息，也就是可能对于区分样本的类别（标签）更有用
3、特征值矩阵的正交向量空间是否唯一有待讨论
4、无监督学习