CSP-J 2024第二轮上机真题

最新推荐文章于 2025-11-06 08:00:00 发布
原创 最新推荐文章于 2025-11-06 08:00:00 发布 · 869 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法

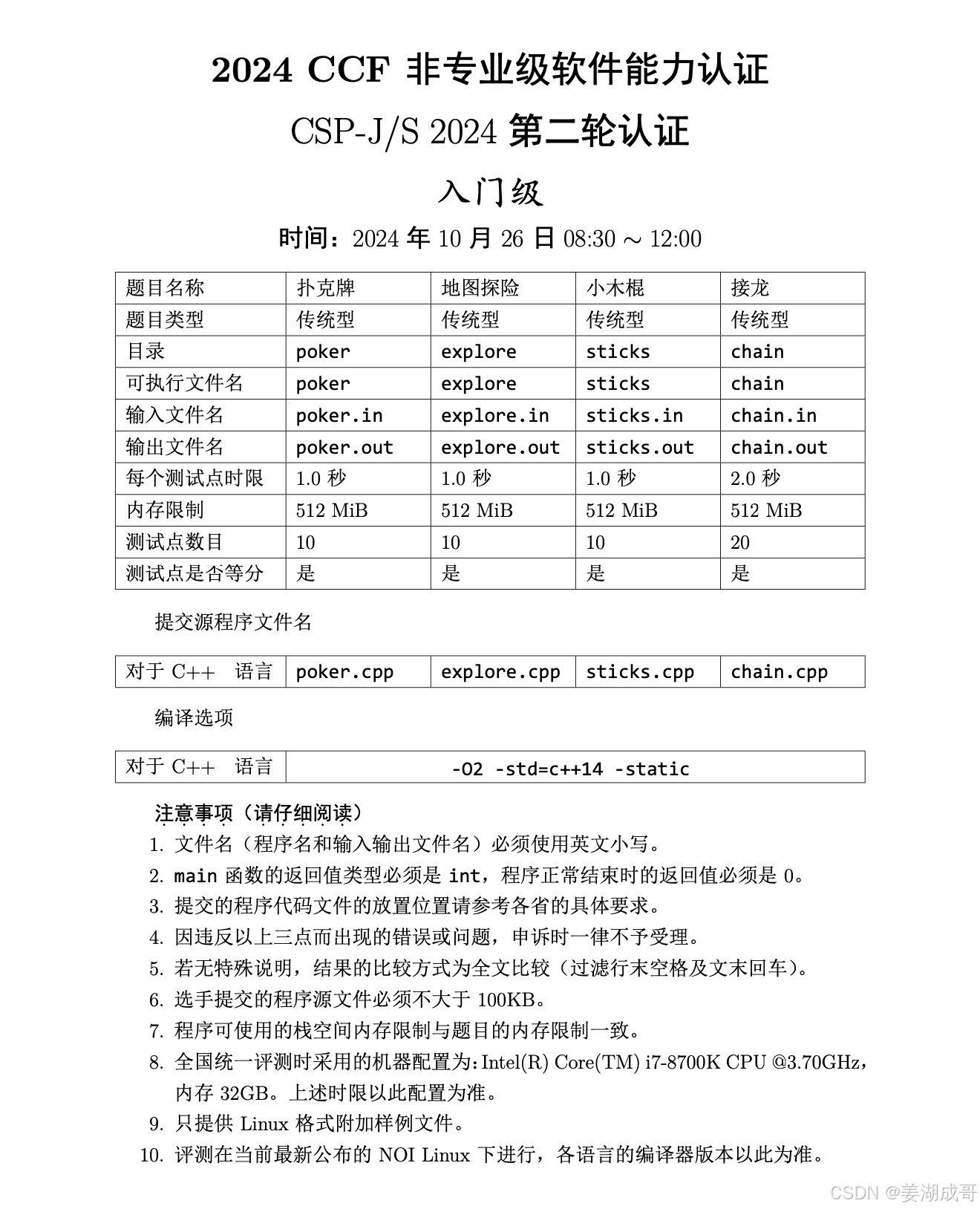
CSP-J 2024真题已出，整体上看，今年的题目也还好：

T1应该说比较简单，没有什么太复杂的，只要会循环、分支、数组，肯定就会做了；

T2稍微复杂一点，不过如果选手练过传统的走迷宫之类的题目，应该说也不难，在走迷宫的过程中，标记有多少个位置即可；

T3应该难一些了，需要花比较多的时间想清楚，用贪心、动态规划的一些思想；

T4要把题目读懂还是需要花点时间的，估计很多选手有难度。

静等洛谷之类的在线OJ。

今年的分数应该也不会低，全国线估计跟去年持平或者高一点？

最低0.47元/天 解锁文章
2022 CSP-J 第二轮认证真题解析
01-02 2378
由于忙于考教资和考研的事情，题目一直没有去做，做完后第一题可以使用快速幂快速求，暴力枚举问题也不大；第二题二分或者韦达定理；第三题最难，中缀转后缀表达式；第四题可以套个floyed或者使用动态规划解决，参考最长上升子序列，2023祝大家RP++。
历年CSP-J第二轮题目
ypeijasd的专栏
10-29 2117
历年CSP-J第二轮题目
CSP-S (NOIP提高组) 历年复赛真题考察内容(1999～2020)
BobHuang的博客
03-20 8175
TZOJ题目分类 1.NOIP2020 T1 排水系统 拓扑排序、高精度 T2 字符串匹配 KMP T3 移球游戏 构造、分治 T4 微信步数 多项式 2.CSP-S 2020 T1 儒略日 大模拟、二分 T2 动物园 二进制 T3 函数调用 拓扑排序、记忆化搜索 T4 贪吃蛇 大模拟、双端队列 3.CSP-S 2019 DAY1 T1 格雷码 模拟 T2 括号树 树型DP T3 树上的数 贪心、深搜 4.CSP-S 2019 DAY2 T1 Emiya 家今天的饭 动态规划(高级) T2 划分 单调队列D
2020 CSP-J2 入门组第二轮试题（ 原noip普及组复赛）
11-07
2020 CSP-J2 入门组第二轮试题（ 原noip普及组复赛）一般来说，一个正整数可以拆分成若干个正整数的和。例如，1 = 1，10 = 1 + 2 + 3 + 4 等。 对于正整数 n 的一种特定拆分，我们称它为“优秀的”，当且仅当在这种拆 分下，n被分解为了若干个不同的 2 的正整数次幂。注意，一个数 x能被表 示成 2 的正整数次幂，当且仅当x能通过正整数个 2 相乘在一起得到。
2025CSP-J 普及组第二轮试题及解析（第三题、异或和（xor））
最新发布
汉克老师的博客
11-06 1402
2025CSP-J 普及组第二轮试题及解析（第三题、异或和（xor））
CSP-J第二轮真题 分类题单
君义NOIP的博客
10-07 1322
以上题单涉及的知识点从上到下为从易到难。每个题单中前面的题较简单，后面的较难。建议先做各题单中的简单的问题，再做较难的问题。每个题单都是一个洛谷竞赛，需要先点报名，输入页面上的邀请码，即可进入。竞赛开放时间到11月初。CSP-J第二轮真题 分类题单。
CSP-J/S-2024第二轮真题分享
IT_Scratch的博客
10-27 205
希望大家能持续关注我们，我们经常会分享一些少儿编程相关的资料。相关资料分享如果有问题，大家可以在文字底部留言整理资料不容易，希望大家多多转发分享往期资料：2024年9月电子学会青少年软件编程（图形化）等级考试试卷（一级）分享青少儿编程资料分享青少儿编程scratch图形化源码分享（8月份合集）...
精选资源
2024年CSP-S第二轮上机真题
10-26
2024年CSP-S第二轮上机真题涉及了信息学奥林匹克竞赛（CCF非专业级软件能力认证CSP-J/S）的相关内容，该赛事主要面向中学阶段的学生，旨在通过编程挑战提升青少年的逻辑思维和编程能力。本次真题内容包含了四个部分...
精选资源
2024 CSP-J2 CSP-S2 复赛 第2轮 机试 常见错误和注意事项等.pdf
10-02
在参与2024 CSP-J2/CSP-S2复赛第二轮机试的过程中，考生需要了解和注意多个方面的内容，以确保他们在比赛中能够发挥出最佳水平并避免不必要的错误。首先，了解比赛的基本规则和目标是至关重要的。CSP-J2和CSP-S2分别...
2024年CSP-S 第二轮上机真题
Jason2012
10-26 627
2024年CSP-S 第二轮上机真题
【CSP】CSP-J 2022 第二轮（复赛）真题解析
雪的期许
11-11 4014
点击查看题目列表 1. 乘方 这道题看似简单，但稍不留神就会出错，要求选手具备全面思考问题的能力。 - 易错点1：如何判断结果超出$$10^9$$? 计算$$a^b$$最直观的做法是使用循环来计算$$b$$个$$a$$相乘，但一定要注意，千万不要等$$b$$个$$a$$相乘结束后再去判断结果是否达到$$10^9$$！因为循环过程中当结果超过$$10^{18}$$（这里假设你定义的数据类型是long long类型）后，就发生了溢出，结果已经出错。解决方法是在循环过程中，每次将结果乘上一个$$a$$，就判断
2024 CCF CSP-J/S 2024 第二轮认证 真题试卷
小码农的博客
10-27 4015
题目总数：4 总分数：400。
2023年CCF非专业级别软件能力认证第二轮 （CSP-J）入门级C++语言试题
No0d1es的博客
11-09 1033
小Z希望乘坐旅游巴士到达景区入口，并沿着自己选择的任意路径走到景区出口，再乘坐旅游巴士离开，这意味着他到达和离开景区的时间都必须是k的非负整数倍。输入的接下来m行，每行包含3个非负整数ui,vi,ai，表示第i条道路从地点ui出发，到达地点vi，道路的“开放时间”为ai。对于所有测试数据有：2≤n≤104，1≤m≤2×104，1≤k≤100，1≤ui,vi≤n，0≤ai≤106。公路上每个站点都可以加油，编号为i的站点一升油的价格为ai元，且每个站点只出售整数升的油。公路上一共有n个站点，编号为从1到n。
CSP-J 2024第二轮认证真题及详解
IT_Scratch的博客
11-01 1354
真题文档请看这篇文章：CSP-J/S-2024第二轮真题分享T1、扑克牌（pocker)T2、地图探险（explore）T3、小木棍（sticks）T4、接龙（chain）
ccf题库java_CCF CSP-J入门级第二轮认证真题及答案（附信奥真题库）-童程童美少儿编程教育...
weixin_36287059的博客
02-27 1210
2019CCF非专业级别软件能力认证第二轮2019 CSP-J 入门级第二轮认证真题解析数字游戏(number)输入文件名：number.in输出文件名：number.out共 20 个测试点，每个测试点 5 分每个测试点限时 1 秒，运行内存上限 256MB问题描述小 K 同学向小 P 同学发送了一个长度为 8 的 01 字符串 来玩数字游戏，小 P 同学想要知道字符串中究竟有多少个 1。注意：...
【题解】CSP-J2021第二轮题解
hexu2010的博客
10-26 1276
CSP-J2021第二轮试题详解
【题解】CSP2022-J第二轮题解
WillHou的博客
11-04 4800
A. 乘方; B. 解密; C. 逻辑表达式; D. 上升点列
csp-j/s 2022 第二轮认证入门级（j）原题
sjy100401的博客
10-03 312
csp-j/s 2022 第二轮认证入门级（j）原题
csp-j2024第一轮
01-26
### CSP-J 2024 第一轮考试信息 #### 报名方式 对于希望参与 CSP-J 2024 的考生而言，报名流程需遵循中国计算机学会 (CCF) 所设定的规定。所有参与者必须在 NOI 官方网站上使用首轮注册账户完成新一轮的报名工作，...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值