10. Regular Expression Matching

题意

给一个主串s和模式串p，看看s和p能否匹配。
p串中存在 ‘.’ 号和 ‘*’ 号，分别代表一个任意字符，以及前一个字符出现任意次。

思路1

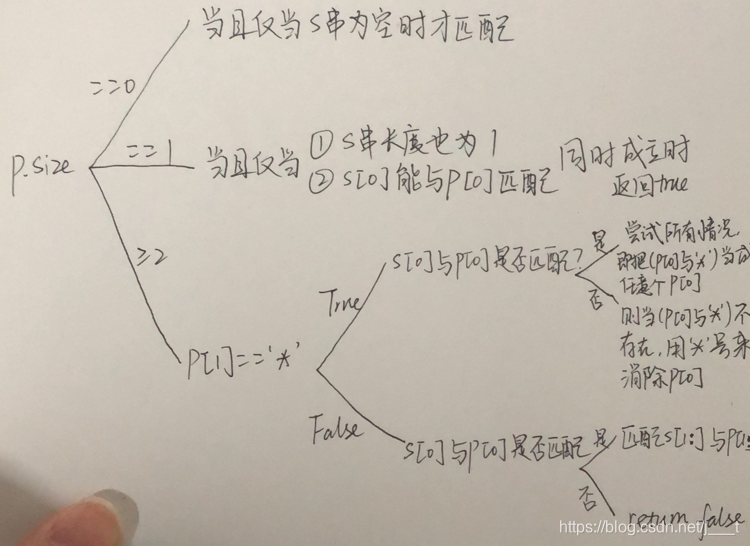
如图所示，根据p的size来分类递归处理。

• 如果s和p都是空的，返回true
• 如果p的大小为1的时候，s.size()==1时并且s[0]能与p[0]匹配时，返回true
• 如果p的大小为2
  – 先看看p[1]是否是’*‘号，如果是的话，则不断将p[0]和’*‘号绑定，不断尝试有0个p[0]，1个p[0]，2个p[0]……只要其中有一种匹配能够成功，那么就返回true。当然，前提是s串第一个字符能和p[0]匹配上。如果匹配不上，则只能使用’*‘号，让p[0]只有0个，即消除p[0]，直接让p从第三个字符开始的子串继续和s匹配
  – 如果p[1]不是’*'号，那么就看看s[0]和p[0]能否匹配，能的话就继续递归下去，否则就return false

时间复杂度：大概是O(n!) 反正很高
考虑如下最坏情况：
s = ‘aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa……’
p = ‘.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*.*……’
对于p中的每一个’.*’，可以和s中的1个，2个，3个……s.size()个a来匹配，而这些匹配由于是递归处理，所以时间开销是相乘的关系，所以时间复杂度大致是O(n!)

代码

class Solution {
public:
    bool isMatch(string s, string p) {
        if (p.empty()) return s.empty();
        if (p.size() == 1)
        {
            if (s.size() == 1 && (p[0] == s[0] || p[0] == '.')) return true;
            else return false;
        }
        if (p[1] != '*')
        {
            if (s.empty()) return false;
            if (p[0] == s[0] || p[0] == '.') return isMatch(s.substr(1), p.substr(1));
            else return false;
        }
        while (s.size() > 0 && (p[0] == s[0] || p[0] == '.'))
        {
            if (isMatch(s, p.substr(2))) return true;
            s = s.substr(1);
        }
        return isMatch(s.substr(0), p.substr(2));
    }
};

思路2

这题的最优解法应该是采取动态规划的方式，状态转移方程如下：

• If p.charAt(j) == s.charAt(i) : dp[i][j] = dp[i-1][j-1];
• If p.charAt(j) == ‘.’ : dp[i][j] = dp[i-1][j-1];
• If p.charAt(j) == ‘*’:
  • if p.charAt(j-1) != s.charAt(i) : dp[i][j] = dp[i][j-2] //in this case, a* only counts as empty
  • if p.charAt(i-1) == s.charAt(i) or p.charAt(i-1) == ‘.’:
    • dp[i][j] = dp[i-1][j] //in this case, a* counts as multiple a
    • or dp[i][j] = dp[i][j-1] // in this case, a* counts as single a
    • or dp[i][j] = dp[i][j-2] // in this case, a* counts as empty

代码

class Solution {
public:
    bool isMatch(string s, string p) {
        s = "#" + s; p = "$" + p;
        int i, j;
        bool dp[1001][1001];
        memset(dp, 0, sizeof(dp));
        dp[0][0] = true;
        for (i = 1; i < p.size(); i++)
        {
            if (p[i] == '*') dp[0][i] = dp[0][i-2];
        }
        for (i = 1; i < s.size(); i++)
        {
            for (j = 1; j < p.size(); j++)
            {
                if (s[i] == p[j] || p[j] == '.') dp[i][j] = dp[i-1][j-1];
                if (p[j] == '*')
                {
                    if (p[j-1] ==s[i] || p[j-1] == '.')
                    {
                        dp[i][j] = dp[i][j-2] || dp[i][j-1] || dp[i-1][j];
                    }
                    else
                    {
                        dp[i][j] = dp[i][j-2];
                    }
                }
                
            }
        }
        return dp[s.size()-1][p.size()-1];
    }
};

参考

https://www.cnblogs.com/grandyang/p/4461713.html
https://leetcode.com/problems/regular-expression-matching/discuss/5684/c-on-space-dp