代码随想录算法训练营第三十四天|LeetCode 62，63

最新推荐文章于 2026-01-05 22:36:07 发布

原创最新推荐文章于 2026-01-05 22:36:07 发布 · 88 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #职场和发展

本文介绍了如何使用动态规划解决LeetCode中的两个问题，62.不同路径和63.不同路径II，涉及dp数组的定义、递推公式、初始化步骤和遍历顺序。着重讲解了在有障碍物的情况下如何调整路径计数。

LeetCode 62.不同路径

文章讲解：代码随想录

视频讲解：动态规划中如何初始化很重要！| LeetCode：62.不同路径_哔哩哔哩_bilibili

力扣题目：LeetCode 62.不同路径

动态规划五部曲：

1.确定dp[i]的含义

dp[m][n]:以第(m,n)格为终点有dp[m][n]种不同的路径

2. 找出递推公式

dp[m][n] = dp[m][n-1] + dp[m-1][n];

3.初始化dp数组

        for(int i = 0; i < m; i++)  dp[i][0] = 1;
        for(int j = 0; j < n; j++)  dp[0][j] = 1;

4.确定遍历方向

从前往后

5.举例dp数组

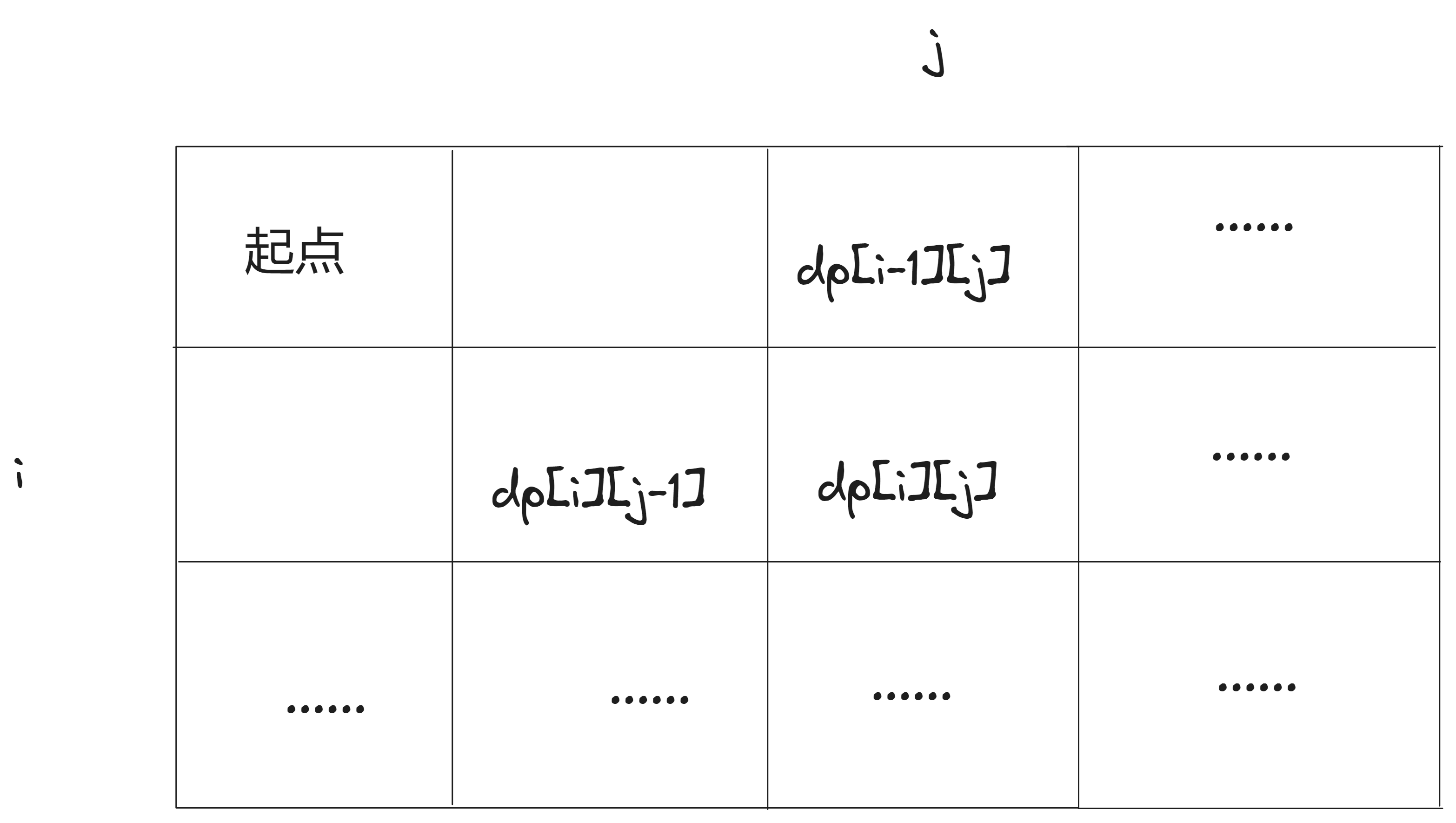
代码如下（Java）：

class Solution {
    public int uniquePaths(int m, int n) {

        int[][] dp = new int[m][n];

        for(int i = 0; i < m; i++)  dp[i][0] = 1;
        for(int j = 0; j < n; j++)  dp[0][j] = 1;

        for(int a = 1; a < m; a++){
            for(int b = 1; b < n; b++){
                dp[a][b] = dp[a-1][b] + dp[a][b-1];
            }
        }

        return dp[m-1][n-1];
    }
}

LeetCode 63.不同路径II

文章讲解：代码随想录

视频讲解：动态规划，这次遇到障碍了| LeetCode：63. 不同路径 II_哔哩哔哩_bilibili

力扣题目：LeetCode 63.不同路径II

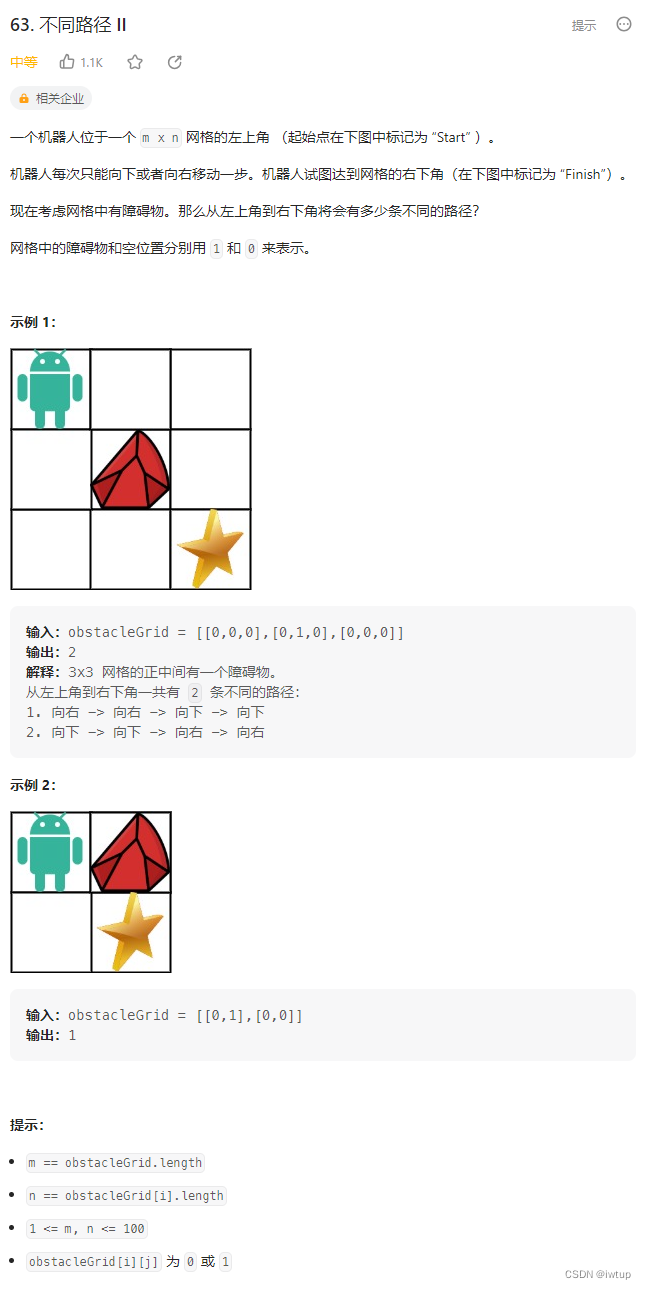
动态规划五部曲：

1.确定dp[i]的意义

dp[i]:到达第i个格子有dp[i]种方法

2.找出递推公式

dp[a][b] = obstacleGrid[a][b] == 0 ? dp[a-1][b] + dp[a][b-1] : 0;

3.初始化dp数组

        for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++)   dp[i][0] = 1;
        for(int j = 0; j < n && obstacleGrid[0][j] == 0; j++)   dp[0][j] = 1;

4.确定遍历顺序

从前往后

5.举例dp数组

代码如下（Java）：

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];

        if(obstacleGrid[m-1][n-1] == 1 || obstacleGrid[0][0] == 1)  return 0;

        for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++)   dp[i][0] = 1;
        for(int j = 0; j < n && obstacleGrid[0][j] == 0; j++)   dp[0][j] = 1;

        for(int a = 1; a < m; a++){
            for(int b = 1; b < n; b++){
                dp[a][b] = obstacleGrid[a][b] == 0 ? dp[a-1][b] + dp[a][b-1] : 0;
            }
        }

        return dp[m-1][n-1];
    }
}