8. 微积分 - 连续

Hi，大家好。

上一节课我们讲了极限，很多小伙伴下来后跟我留言说有点懵。不必太过在意，慢慢的多看几遍去理解，并且，极限也并不是特别核心的问题，暂时先放一放也可以。

本节课，我们要讲的内容是「连续」。

连续

首先，我们从直观上想一下，在日常生活里面这个连续它给我们一些什么样的印象？可能会优先想到这么几点：

• 一个是不断裂。
• 其次是不跳跃
• 处处相连

那咱们先来看看不断裂。打比方说，本来有这么一个函数图像好好的，但是我们在它中间断了一个点，就这么一个点就是一个老鼠屎坏了一锅粥。连续就应该是不断裂的，不能象下面这个例子一样：

第二点是不跳跃。我们来看下面这张函数图：

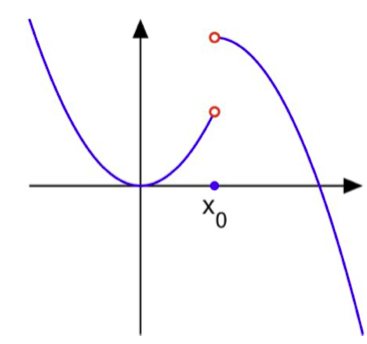
这个函数本来在前面一节的时候，在 x 0 x_0