数据结构与算法学习笔记——图(Graph)

什么是图:

                                   

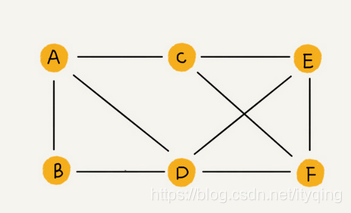
                                   无向图:可以理解QQ中的互加好友

                                  

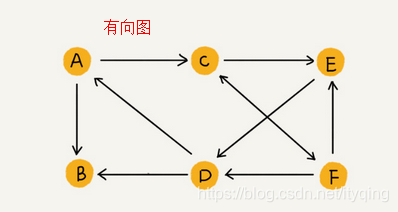
                                    无向图: 可以理解为微博中的关注

图的一些概念:

顶点:图中的元素(A,B,C,D....)

边: 图中的一个顶点可以与任意其他顶点建立连接关系,这种建立的关系就是边

度: 与顶点相连接的边的条数(无向图概念)(图一A的度就是3)

无向图: 边无方向的图

有向图: 边有方向的图

稀疏图(Sparse Matrix) : 顶点很多,但每个顶点的边并不多

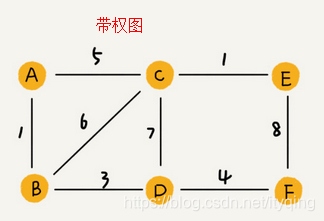
带权图(weighted graph) 。在带权图中,每条边都有一个权重 (weight)

                                   

有向图的一些概念:

入度(In-degree) : 表示有多少条边指向这个顶点

出度(Out-degre) : 表示有多少条边是以这个顶点为起点推向其他顶点

图的存储:  

    邻接矩阵(Adjacency Matrix):

    邻接矩阵的底层依赖一个二维数组。对于无向图来说，如果顶点 i 与顶点 j 之间有边，我们就将 A[i][j] 和 A[j][i] 标记为 1；对于有向图来说，如果顶点 i 到顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，那我们就将 A[i][j] 标记为 1。同理，如果有一条箭头从顶点 j 指向顶点 i 的边，我们就将 A[j][i] 标记为 1。对于带权图，数组中就存储相应的权重。

                                   

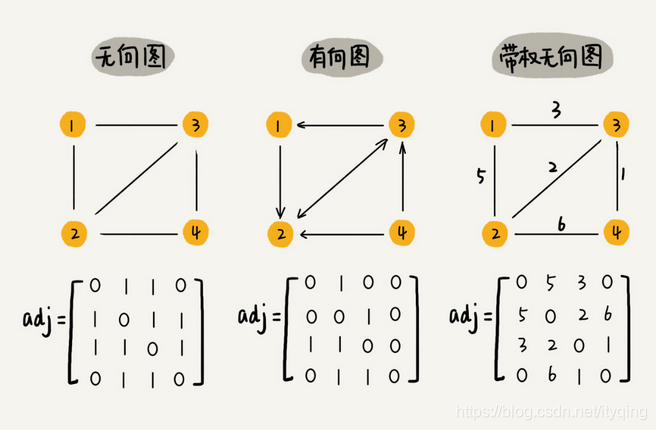
优点: 简单直观,

缺点:浪费空间

无向图,如:A[i][j] 和 A[j][i] 只需一个就行了。

稀疏图：顶点很多，但每个顶点的边并不多。

邻接表存储法:

每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点。

            

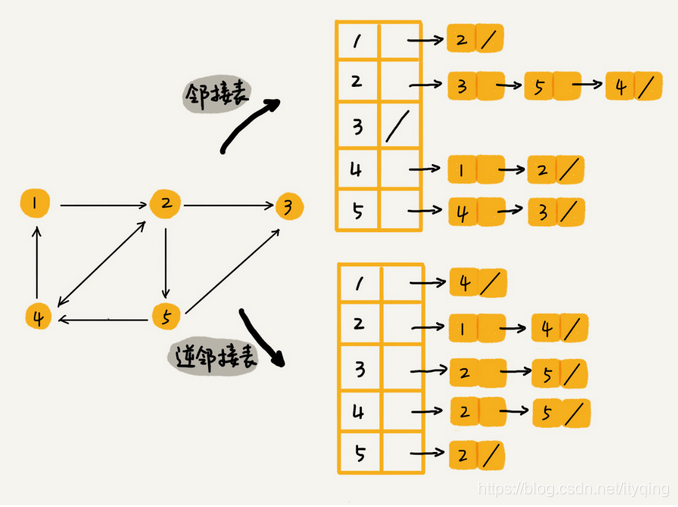
邻接矩阵存储起来比较浪费空间，但是使用起来比较节省时间。相反，邻接表存储起来比较节省空间，但是使用起来就比较耗时间。