每日ACM学习以及小水题 2013年11月3日

说明

为了向大神看齐，遂响应号召，每天刷一下POJ上面的水题，每天学习一点ACM，做一点ACM题目。

我相信积少成多，更相信，开头是艰难的，但是一旦走进去，就会别有一番感受，速度也会加快吧。

so ，today is the first day .

题目

第一题

POJ 1003 （传送门：http://poj.org/problem?id=1003）

题目描述：

Description

How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2+1/3=5/6 card lengths. In general you can makencards overhang by 1/2+1/3+1/4+...+1/(n+1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n+1). This is illustrated in the figure below.

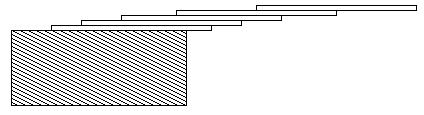
Input

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

第二题

找所有的(n, k), 满足:1+2+..+(n-1)=(n+1)+(n+2)…+k 。输出按k排序的前6个。

解答过程

第一题：简答的数学题

代码如下：

/*****  简单ACM水题 ********/

/******** written by C_Shit_Hu ************/

////////////////POJ 1003///////////////

/****************************************************************************/
/* 
求平均数。
*/
/****************************************************************************/

#include <iostream>
using namespace std;

int main()
{ 
	int i;
	float len,s;
	while(cin >> len && len != 0.00)
	{
		s = 0.0;
		for(i = 2; ; i++)
		{
			s+=1.0/i;
			if(s >= len)
				break;
		}
		cout << i-1 <<" card(s)" << endl;
	}
	return 0;
}

运行结果：

第二题:数论相关的题目

【分析过程】

整理得: n(n-1)=(k-n)(n+k+1)，化简得: k2+k-2n2=0, 即n2=k(k+1)/2，

由于k和k+1互素, 因此
----要么k是完全平方数
----要么k/2是完全平方数
分别设k=m2和2m2, 枚举m

代码如下：

/*****  简单ACM水题 ********/

/******** written by C_Shit_Hu ************/

///////////////////////////////

/****************************************************************************/
/* 
找所有的(n, k), 满足:
1+2+..+(n-1)=(n+1)+(n+2)…+k
输出按k排序的前10个
*/
/****************************************************************************/

#include <iostream>
#include <cmath>
using namespace std;

bool sing(int  j)
{
	long int k, n;
	double m;
	k = j * j;
	n = k*(k+1) / 2;
	m = sqrt(n);
	if ( floor(m + 0.5) == m)
	{
	//	printf("n = %d, k = %d\n", m, k);
		cout << m << " " << k  << endl;
		return true;
	}
	else
		return false;
}

bool doub(int j)
{
	long int k, n;
	double m;
	k = 2 * j * j;
	n = k*(k+1) / 2;
	m = sqrt(n);
	if ( floor(m + 0.5) == m)
	{
		cout << m << " " << k  << endl;
		return true;
	}
	else
		return false;
}

int main( )
{
	// freopen("in.txt","r",stdin);
	// freopen("out.txt","w",stdout);
	int i, j;
		for (i=1,j=1; i< 7 ; j++)
		{
			if(sing(j))
				i ++ ;
			if(doub(j))
				i ++ ;
		}
	return 0;
}




/******************************************************/
/********************  心得体会  **********************/
/*

*/
/******************************************************/

运行结果：

【未完待续】..............