2016.08.20
上课内容:哈夫曼树
哈夫曼树(霍夫曼树)又称为最优二叉树.
1、路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长
2、结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL
WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln)
N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。
哈夫曼树的形式如图1所示:
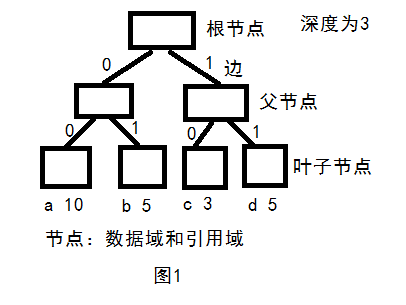
父节点(parent)又分为左节点(left)和右节点(right),其遍历方式有四种,即:前序遍历,中序遍历,后续遍历,层次遍历
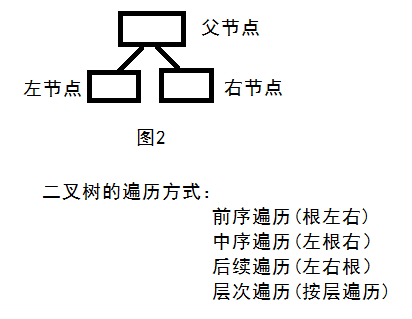
图3为带权路径长度的算法,哈夫曼树的带权路径最短。
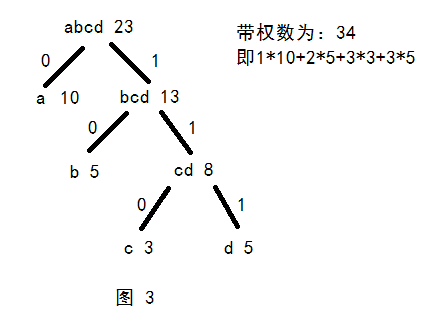
练习:找出哈夫曼树的节点和带权值
import java.util.*;
public class HuffmanTree
{
public static class Node<E>
{
E data;
double weight;
Node leftChild;
Node rightChild;
public Node(E data , double weight)
{
this.data = data;
this.weight = weight;
}
public String toString()
{
return "Node[数字:" + data + " 频率:" + weight + "]";
}
}
public static void main(String[] args)
{
List<Node> nodes = new ArrayList<Node>();
nodes.add(new Node("A" , 40.0));
nodes.add(new Node("B" , 8.0));
nodes.add(new Node("C" , 10.0));
nodes.add(new Node("D" , 30.0));
nodes.add(new Node("E" , 10.0));
nodes.add(new Node("F" , 2.0));
Node root = HuffmanTree.createTree(nodes);
System.out.println(breadthFirst(root));
}
/**
* 构造哈夫曼树
* @param nodes 节点集合
* @return 构造出来的哈夫曼树的根节点
*/
private static Node createTree(List<Node> nodes)
{
//只要nodes数组中还有2个以上的节点
while (nodes.size() > 1)
{
quickSort(nodes);
//获取权值最小的两个节点
Node left = nodes.get(nodes.size() - 1);
Node right = nodes.get(nodes.size() - 2);
//生成新节点,新节点的权值为两个子节点的权值之和
Node parent = new Node(null , left.weight + right.weight);
//让新节点作为权值最小的两个节点的父节点
parent.leftChild = left;
parent.rightChild = right;
//删除权值最小的两个节点
nodes.remove(nodes.size() - 1);
nodes.remove(nodes.size() - 1);
//将新生成的父节点添加到集合中
nodes.add(parent);
}
//返回nodes集合中唯一的节点,也就是根节点
return nodes.get(0);
}
//将指定数组的i和j索引处的元素交换
private static void swap(List<Node> nodes, int i, int j)
{
Node tmp;
tmp = nodes.get(i);
nodes.set(i , nodes.get(j));
nodes.set(j , tmp);
}
//实现快速排序算法,用于对节点进行排序。从大到小的排序
private static void subSort(List<Node> nodes, int start , int end)
{
//需要排序
if (start < end)
{
//以第一个元素作为分界值
Node base = nodes.get(start);
//i从左边搜索,搜索大于分界值的元素的索引
int i = start;
//j从右边开始搜索,搜索小于分界值的元素的索引
int j = end + 1;
while(true)
{
//找到大于分界值的元素的索引,或i已经到了end处
while(i < end && nodes.get(++i).weight >= base.weight);
//找到小于分界值的元素的索引,或j已经到了start处
while(j > start && nodes.get(--j).weight <= base.weight);
if (i < j)
{
swap(nodes , i , j);
}
else
{
break;
}
}
swap(nodes , start , j);
//递归左子序列
subSort(nodes , start , j - 1);
//递归右边子序列
subSort(nodes , j + 1, end);
}
}
public static void quickSort(List<Node> nodes)
{
subSort(nodes , 0 , nodes.size() - 1);
}
//广度优先遍历
public static List<Node> breadthFirst(Node root)
{
Queue<Node> queue = new ArrayDeque<Node>();
List<Node> list = new ArrayList<Node>();
if( root != null)
{
//将根元素入“队列”
queue.offer(root);
}
while(!queue.isEmpty())
{
//将该队列的“队尾”的元素添加到List中
list.add(queue.peek());
Node p = queue.poll();
//如果左子节点不为null,将它加入“队列”
if(p.leftChild != null)
{
queue.offer(p.leftChild);
}
//如果右子节点不为null,将它加入“队列”
if(p.rightChild != null)
{
queue.offer(p.rightChild);
}
}
return list;
}
}
哈夫曼树的应用:
在通信及数据传输中多采用二进制编码。为了使电文尽可能的缩短,可以对电文中每个字符出现的次数进行统计。设法让出现次数多的字符的二进制码短些,而让那些很少出现的字符的二进制码长一些。
在数中令左边分支去编码为0,右边编码为1,将从根节点到某个叶子节点上的各左、右分支的编码顺序排列,就得到这个叶子节点所代表的字符的二进制编码,如图4所示。
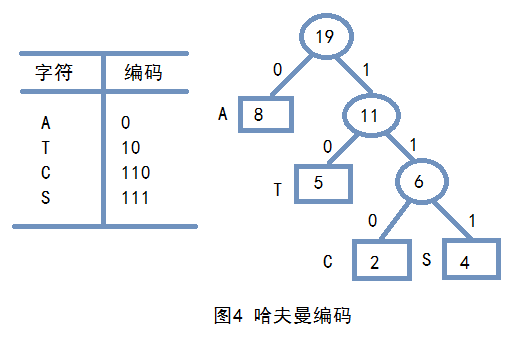
这些编码拼成的电文不会混淆,因为每个字符的编码不是其它编码的前缀,这种编码称为前缀编码。





















 1704
1704

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








