哈夫曼树

原创已于 2022-07-20 22:24:04 修改 · 1.3w 阅读

46 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构

于 2022-07-20 22:21:30 首次发布

数据结构与算法专栏收录该内容

1 篇文章

订阅专栏

本文介绍了哈夫曼树的定义、构造过程，以及它在数据压缩中的应用，包括哈夫曼编码的原理和实际示例。通过哈夫曼树的构建，我们展示了如何利用最小带权路径长度实现文本数据的有效压缩。

哈夫曼树

1，简介

我们日常在对文件进行压缩时，它的压缩原理简单的说就是把我们要压缩的文本进行重新编码，以减少不必要的空间。

尽管现在最新技术在编码上已经很好很强大，但我们平时所用的压缩和解压缩技术也都是基于哈夫曼的研究之上发展而来。

在编码中用到的特殊的二叉树称之为哈夫曼树，他的编码方法称为哈夫曼编码。

哈夫曼树为美国数学家哈夫曼（David Huffman）也有的翻译为赫夫曼的巨佬开创的。

2，哈夫曼树定义与原理

[1]一些名词概念：

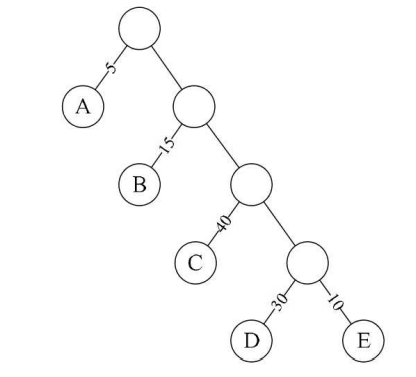
路径：可以理解为两个节点相连的线

某个节点路径长度：两个节点中间隔线条数（如上图根结点到结点D最短间隔四条线，那么D的路径长度就为4）

树的路径长度：如上图二叉树的树路径长度就为1+1+2+2+3+3+4+4=20

结点的带权路径长度：从该结点到树根之间的路径长度与结点上权的乘积

树的带权路径长度：为树中所有叶子结点的带权路径长度之和（计算公式如下）
$W P L = \sum i = 1 n w i l i$
其中，n表示叶子结点的数目，wi和li分别表示叶子结点ki的权值和树根结点到kiwi和li分别表示叶子结点ki的权值和树根结点到ki之间的路径长度，带权路径长度WPL最小的二叉树就称做哈夫曼树

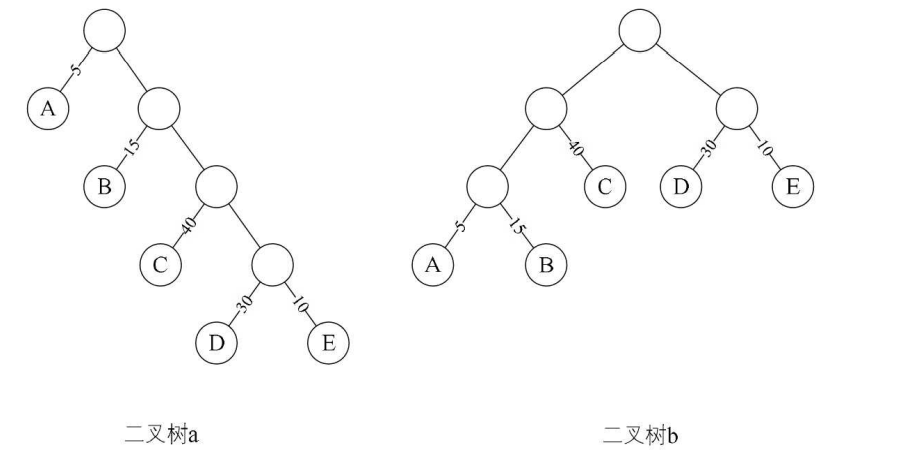
例如下面二叉树的WPL值：

二叉树a的WPL=5×1+15×2+40×3+30×4+10×4=315（5是A结点的权，1是A结点的路径长度）

二叉树b的WPL=5×3+15×3+40×2+30×2+10×2=220

[2]如何判断一颗树为哈夫曼树

先把有权值的叶子结点按照从小到大的顺序排列成一个有序序列，即：A5，E10，B15，D30，C40。
取头两个最小权值的结点作为一个新节点N1的两个子结点，注意相对较小的是左孩子，这里就是A为N1的左孩子，E为N1的右孩子.新结点的权值为两个叶子权值的和5+10=15。

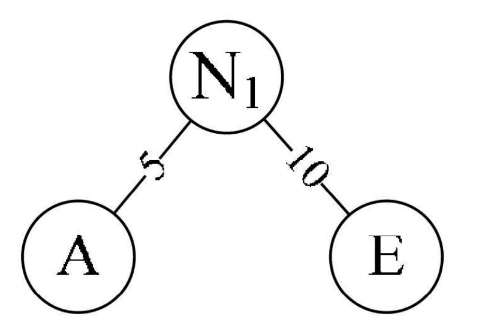
将N1替换A与E，插入有序序列中，保持从小到大排列。即： N115，B15，D30，C40。
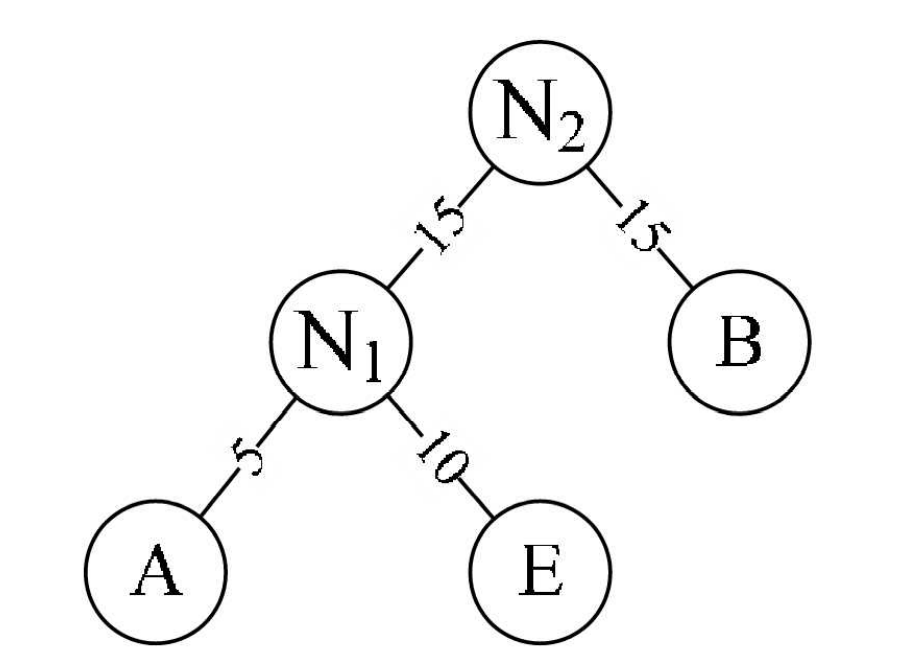
重复步骤2。将N1与B作为一个新节点N2的两个子结点。如下图所示。N2的权值=15+15=30

将N2替换N1与B，插入有序序列中，保持从小到大排列。即： N230，D30，C40
重复步骤2。将N2与D作为一个新节点N3的两个子结点。如图6-12- 7所示。N3的权值=30+30=60
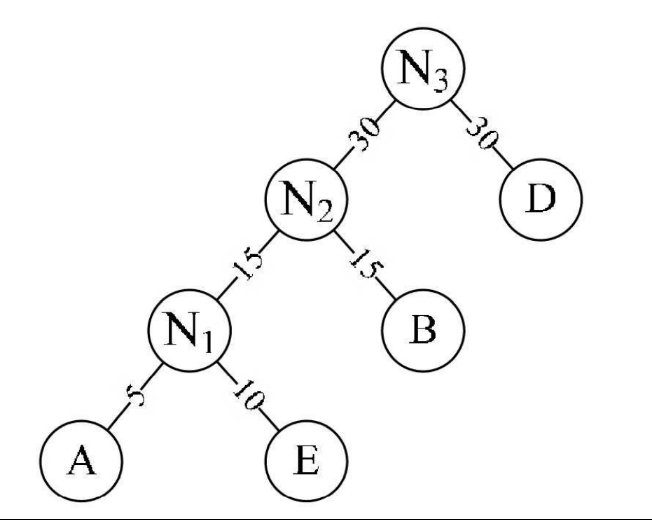
将N3替换N2与D，插入有序序列中，保持从小到大排列。即： C40，N360。
重复步骤2。将C与N3作为一个新节点T的两个子结点，如图6-12-8 所示。由于T即是根结点，完成赫夫曼树的构造。

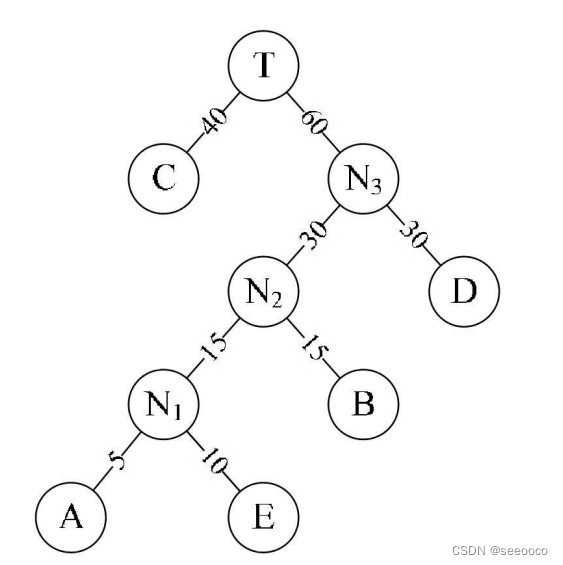
在这里插入图片描述

经过这一些列步骤后的为WPL=40×1+30×2+15×3+10×4+5×4=205。与上面二叉树b的 WPL值220相比，还少了15。显然此时构造出来的二叉树才是最优的哈夫曼树。

[3]哈夫曼算法描述

1.根据给定的n个权值{w1 ,w2 ,…,wn }构成n棵二叉树的集合F= {T1 ,T2 ,…,Tn }，其中每棵二叉树Ti中只有一个带权为wi根结点，其左右子树均为空。

2.在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。

3.在F中删除这两棵树，同时将新得到的二叉树加入F中。

4.重复2和3步骤，直到F只含一棵树为止。这棵树便是赫夫曼树。

3，哈夫曼编码

[1]编码

赫夫曼研究这种最优树的目的是为了解决当年远距离通信（主要是电报）的数据传输的最优化问题。

比如我们有一段文字内容为“BADCADFEED”要网络传输给别人，我们都知道这将会转为二进制的数字（0和1）表示来传递。

原来的二进制转换为

在这里插入图片描述

这样真正传输的数据就是编码后的“001000011010000011101100100011”，

现在假设六个字母的频率为A 27，B 8，C 15，D15，E 30，F 5，那么便可以使用哈夫曼树来规划它们了。

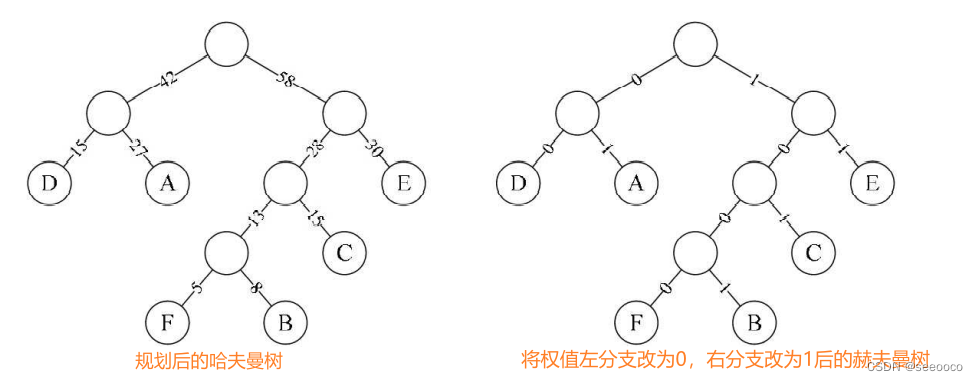
在这里插入图片描述

我们对这六个字母用其从树根到叶子所经过路径的0或1来编码，这样这串字母通过哈夫曼编码后为1001010010101001000111100（共25个字符）相比之前的默认编码001000011010000011101100100011（共30个字符）可以看出数据被压缩了，节约了大约17%的存储或传输成本

[2]解码

前缀编码：任一字符的编码都不是另一个字符的编码的前缀

在解码时，还是要用到赫夫曼树，即发送方和接收方必须要约定好同样的赫夫曼编码规则。

当我们接收到1001010010101001000111100时，由约定好的赫夫曼树可知，1001得到第一个字母是B，接下来01意味着第二个字符是 A，如图6-12-10所示，其余的也相应的可以得到，从而成功解码

[3]小结

一般地，设需要编码的字符集为{d1 ,d2 ,…,dn }，各个字符在电文中出现的次数或频率集合为{w1 ,w2 ,…,wn }，以d1 ,d2 ,…,dn作为叶子结点，以 w1 ,w2 ,…,wn作为相应叶子结点的权值来构造一棵赫夫曼树。规定赫夫曼树的左分支代表0，右分支代表1，则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码，这就是赫夫曼编码。