Description

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!
Input
Output
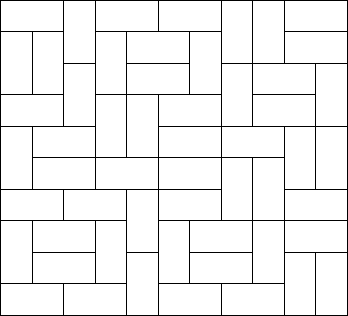 For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical
tilings multiple times.
For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical
tilings multiple times.Sample Input
1 2 1 3 1 4 2 2 2 3 2 4 2 11 4 11 0 0
Sample Output
1 0 1 2 3 5 144 51205
1<=h,w<=11. 数据限制较小,可以用状态压缩方法。
首先 我们先求用1*2 的矩形拼成 n*m的矩形有多少种拼法
分两个步骤, 1) 先求出相邻两行的转化关系
2) 通过相邻两行的转化关系算出经过n次转化有几种方法能拼成n*m的矩阵
在别人的基础上再做些解释:
1) 状态标记 横放占两位都为1,竖放占一位为1(上1下0),不放置占两位都为0,每行可以转化为1个2进制数。
当该行放完时,即队应 11111 (m个), 即2^m-1, dp[n][2^m-1] 即最终结果。
竖放的只所以占一位,是由于我们是从左下角往右上角递推,此处可以竖放说明它的前一行此处必然没放置,即为0.
此行的计算,只需由前一行递推可得。因此可用滚动数组节省一点内存(非重点)。
//根据横放和竖放,可以把每行根据01合成一个二进制数,其实就是状态压缩。
对于每一个位置,我们有三种放置方法:
1. 竖直放置
2. 水平放置
3. 不放置
d为当前列号 ,初始化d, s1, s2都为0;对应以上三种放置方法,s1, s2的调整为: s1 为当前行, s2为当前行的上一行
1. d = d + 1, s1 << 1 | 1, s2 << 1; // 竖直放置 当前行为1,上一行为0
2. d = d + 2, s1 << 2 | 3, s2 << 2 | 3; // 横放 都为11(11=3)
3. d = d + 1, s1 << 1, s2 << 1 | 1; // 上一行为1,不能竖放,不放置的状态(竖放为出现不能放置的情况,横放可以一直向右拓展,越界则不计算即可)
// s1<<1 | 1 意思是,先把s1左移1位,然后位运算或上 1的二进制数,即 01 。
另外:第一行单独计算//============================================================================
// Name : POJ2411.cpp
// Author :
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//============================================================================
#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
int const MAXN = (1 << 11);
__int64 dp[11][4100];
int m,n,row;
void dfs(int c,int s,int ps){
if(c > m) return;
if(c == m){
dp[row][s] += dp[row-1][ps];
return;
}
dfs(c+1, s<<1, (ps << 1) | 1); //不放
dfs(c+1, (s<<1) | 1, ps << 1); //竖放
dfs(c+2, (s<<2) | 3, ps << 2 | 3); //横放
}
void dfs_first(int c,int s){
if(c > m) return;
if(c == m){
dp[0][s] = 1;
}
dfs_first(c+1, s<<1); //不放
dfs_first(c+2, (s<<2) | 3); //横放
}
int main() {
freopen("in.txt", "r", stdin);
int i;
while(scanf("%d %d", &m, &n),m){
if(m*n % 2){
puts("0"); continue;
}
if(m < n) swap(m,n);
memset(dp, 0, sizeof(dp));
dfs_first(0,0);
for(i=1; i<n; i++)
{
row = i;
dfs(0,0,0);
}
printf("%I64d\n", dp[n-1][(1<<m) -1]);
}
return 0;
}




 本文探讨了著名荷兰画家皮特·蒙德里安使用矩形进行艺术创作的过程,特别关注他在尝试用宽度为2、高度为1的矩形填充更大矩形时所面临的挑战。通过引入计算机辅助的方法来解决此类问题,作者提供了一种高效算法,以计算特定尺寸矩形的不同填充方式。此外,文章还详细解释了如何利用状态压缩技巧简化计算过程,并给出了具体的实现代码。
本文探讨了著名荷兰画家皮特·蒙德里安使用矩形进行艺术创作的过程,特别关注他在尝试用宽度为2、高度为1的矩形填充更大矩形时所面临的挑战。通过引入计算机辅助的方法来解决此类问题,作者提供了一种高效算法,以计算特定尺寸矩形的不同填充方式。此外,文章还详细解释了如何利用状态压缩技巧简化计算过程,并给出了具体的实现代码。
















 285
285

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








