http://mathworld.wolfram.com/SmoothFunction.html
| Smooth Function | |
A smooth function is a function that has continuous derivatives up to some desired order over some domain. A function can therefore be said to be smooth over a restrictedinterval such as![]() or
or![]() . The number of continuous derivatives necessary for a function to be considered smooth depends on the problem at hand, and may vary from two to infinity. A function for which all orders of derivatives are continuous is called aC-infty-function.
. The number of continuous derivatives necessary for a function to be considered smooth depends on the problem at hand, and may vary from two to infinity. A function for which all orders of derivatives are continuous is called aC-infty-function.
SEE ALSO: C-infty-Function, Continuous Function, Derivative, Function
http://en.wikipedia.org/wiki/Smooth_function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.
Most of this article is about real-valued functions of one real variable. A discussion of the multivariable case is presented towards the end.
Contents[hide] |
[edit] Differentiability classes
Consider an open set on the real line and a function f defined on that set with real values. Let k be a non-negative integer. The function f is said to be of class Ck if the derivatives f', f'', ..., f(k) exist and are continuous (the continuity is automatic for all the derivatives except for f(k)). The function f is said to be of class C∞, or smooth, if it has derivatives of all orders.[1]f is said to be of class Cω, or analytic, if f is smooth and if it equals its Taylor series expansion around any point in its domain.
To put it differently, the class C0 consists of all continuous functions. The class C1 consists of all differentiable functions whose derivative is continuous; such functions are called continuously differentiable. Thus, a C1 function is exactly a function whose derivative exists and is of class C0. In general, the classes Ck can be defined recursively by declaring C0 to be the set of all continuous functions and declaring Ck for any positive integer k to be the set of all differentiable functions whose derivative is in Ck−1. In particular, Ck is contained in Ck−1 for every k, and there are examples to show that this containment is strict. C∞ is the intersection of the sets Ck as k varies over the non-negative integers. Cω is strictly contained in C∞; for an example of this, see bump function or also below.
[edit] Examples
The function
is continuous, but not differentiable at  , so it is of class C0 but not of class C1.
, so it is of class C0 but not of class C1.
The function
is differentiable, with derivative
Because cos(1/x) oscillates as x approaches zero, f ’(x) is not continuous at zero. Therefore, this function is differentiable but not of class C1. Moreover, if one takes f(x) = x3/2 sin(1/x) (x ≠ 0) in this example, it can be used to show that the derivative function of a differentiable function can be unbounded on a compact set and, therefore, that a differentiable function on a compact set may not be locally Lipschitz continuous.
The functions
- f(x) = | x | k + 1
where k is even, are continuous and k times differentiable at all x. But at  they are not (k+1) times differentiable, so they are of class C k but not of class C j where j>k.
they are not (k+1) times differentiable, so they are of class C k but not of class C j where j>k.
The exponential function is analytic, so, of class Cω. The trigonometric functions are also analytic wherever they are defined.
The function
is smooth, so of class C∞, but it is not analytic at  , so it is not of class Cω. The function f is an example of a smooth function with compact support.
, so it is not of class Cω. The function f is an example of a smooth function with compact support.
[edit] Multivariate differentiability classes
Let n and m be some positive integers. If f is a function from an open subset of Rn with values in Rm, then f has component functions f1, ..., fm. Each of these may or may not have partial derivatives. We say that f is of class Ck if all of the partial derivatives  exist and are continuous, where each of
exist and are continuous, where each of 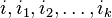 is an integer between 1 and n, each of
is an integer between 1 and n, each of 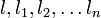 is an integer between 0 and k,
is an integer between 0 and k, 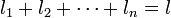 .[1] The classes C∞ and Cω are defined as before.[1]
.[1] The classes C∞ and Cω are defined as before.[1]
These criteria of differentiability can be applied to the transition functions of a differential structure. The resulting space is called a Ckmanifold.
If one wishes to start with a coordinate-independent definition of the class Ck, one may start by considering maps between Banach spaces. A map from one Banach space to another is differentiable at a point if there is an affine map which approximates it at that point. The derivative of the map assigns to the point x the linear part of the affine approximation to the map at x. Since the space of linear maps from one Banach space to another is again a Banach space, we may continue this procedure to define higher order derivatives. A map f is of class Ck if it has continuous derivatives up to order k, as before.
Note that Rn is a Banach space for any value of n, so the coordinate-free approach is applicable in this instance. It can be shown that the definition in terms of partial derivatives and the coordinate-free approach are equivalent; that is, a function f is of class Ck by one definition iff it is so by the other definition.
[edit] The space of Ck functions
Let D be an open subset of the real line. The set of all Ck functions defined on 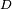 and taking real values is a Fréchet space with the countable family of seminorms
and taking real values is a Fréchet space with the countable family of seminorms
where K varies over an increasing sequence of compact sets whose union is D, and m = 0, 1, …, k.
The set of C∞ functions over 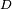 also forms a Fréchet space. One uses the same seminorms as above, except that
also forms a Fréchet space. One uses the same seminorms as above, except that 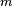 is allowed to range over all non-negative integer values.
is allowed to range over all non-negative integer values.
The above spaces occur naturally in applications where functions having derivatives of certain orders are necessary; however, particularly in the study of partial differential equations, it can sometimes be more fruitful to work instead with the Sobolev spaces.
[edit] Parametric continuity
Parametric continuity is a concept applied to parametric curves describing the smoothness of the parameter's value with distance along the curve.
[edit] Definition
A curve can be said to have Cn continuity if
is continuous of value throughout the curve.
As an example of a practical application of this concept, a curve describing the motion of an object with a parameter of time, must have C1 continuity for the object to have finite acceleration. For smoother motion, such as that of a camera's path while making a film, higher levels of parametric continuity are required.
[edit] Order of continuity

The various order of parametric continuity can be described as follows:[2]
- C−1: curves include discontinuities
- C0: curves are joined
- C1: first derivatives are equal
- C2: first and second derivatives are equal
- Cn: first through nth derivatives are equal
The term parametric continuity was introduced to distinguish it from geometric continuity (Gn) which removes restrictions on the speed with which the parameter traces out the curve.[3]
[edit] Geometric continuity
The concept of geometrical or geometric continuity was primarily applied to the conic sections and related shapes by mathematicians such as Leibniz, Kepler, and Poncelet. The concept was an early attempt at describing, through geometry rather than algebra, the concept of continuity as expressed through a parametric function.
The basic idea behind geometric continuity was that the five conic sections were really five different versions of the same shape. An ellipse tends to a circle as the eccentricity approaches zero, or to a parabola as it approaches one; and a hyperbola tends to a parabola as the eccentricity drops toward one; it can also tend to intersecting lines. Thus, there was continuity between the conic sections. These ideas led to other concepts of continuity. For instance, if a circle and a straight line were two expressions of the same shape, perhaps a line could be thought of as a circle of infinite radius. For such to be the case, one would have to make the line closed by allowing the point x = ∞ to be a point on the circle, and for x = +∞ and x = −∞ to be identical. Such ideas were useful in crafting the modern, algebraically defined, idea of the continuity of a function and of ∞.
[edit] Smoothness of curves and surfaces
A curve or surface can be described as having Gn continuity, n being the increasing measure of smoothness. Consider the segments either side of a point on a curve:
- G0: The curves touch at the join point.
- G1: The curves also share a common tangent direction at the join point.
- G2: The curves also share a common center of curvature at the join point.
In general, Gn continuity exists if the curves can be reparameterized to have Cn (parametric) continuity.[4] A reparametrization of the curve is geometrically identical to the original; only the parameter is affected.
Equivalently, two vector functions 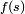 and
and  have Gn continuity if
have Gn continuity if 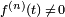 and
and  , for a scalar
, for a scalar  (i.e., if the direction, but not necessarily the magnitude, of the two vectors is equal).
(i.e., if the direction, but not necessarily the magnitude, of the two vectors is equal).
While it may be obvious that a curve would require G1 continuity to appear smooth, for good aesthetics, such as those aspired to in architecture and sports car design, higher levels of geometric continuity are required. For example, reflections in a car body will not appear smooth unless the body has G2 continuity.[citation needed]
A rounded rectangle (with ninety degree circular arcs at the four corners) has G1 continuity, but does not have G2 continuity. The same is true for a rounded cube, with octants of a sphere at its corners and quarter-cylinders along its edges. If an editable curve with G2 continuity is required, then cubic splines are typically chosen; these curves are frequently used in industrial design.
[edit] Smoothness
[edit] Relation to analyticity
While all analytic functions are smooth on the set on which they are analytic, the above example shows that the converse is not true for functions on the reals: there exist smooth real functions which are not analytic. For example, the Fabius function is smooth but not analytic at any point. Although it might seem that such functions are the exception rather than the rule, it turns out that the analytic functions are scattered very thinly among the smooth ones; more rigorously, the analytic functions form a meagre subset of the smooth functions. Furthermore, for every open subset A of the real line, there exist smooth functions which are analytic on A and nowhere else.
It is useful to compare the situation to that of the ubiquity of transcendental numbers on the real line. Both on the real line and the set of smooth functions, the examples we come up with at first thought (algebraic/rational numbers and analytic functions) are far better behaved than the majority of cases: the transcendental numbers and nowhere analytic functions have full measure (their complements are meagre).
The situation thus described is in marked contrast to complex differentiable functions. If a complex function is differentiable just once on an open set it is both infinitely differentiable and analytic on that set.
[edit] Smooth partitions of unity
Smooth functions with given closed support are used in the construction of smooth partitions of unity (see partition of unity and topology glossary); these are essential in the study of smooth manifolds, for example to show that Riemannian metrics can be defined globally starting from their local existence. A simple case is that of a bump function on the real line, that is, a smooth function f that takes the value 0 outside an interval [a,b] and such that
Given a number of overlapping intervals on the line, bump functions can be constructed on each of them, and on semi-infinite intervals (-∞, c] and [d,+∞) to cover the whole line, such that the sum of the functions is always 1.
From what has just been said, partitions of unity don't apply to holomorphic functions; their different behavior relative to existence and analytic continuation is one of the roots of sheaf theory. In contrast, sheaves of smooth functions tend not to carry much topological information.
[edit] Smooth functions between manifolds
Smooth maps between smooth manifolds may be defined by means of charts, since the idea of smoothness of function is independent of the particular chart used. If F is a map from an m-manifold M to an n-manifold N, then F is smooth if, for every  , there is a chart
, there is a chart  in M containing p and a chart
in M containing p and a chart 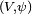 in N containing F(p) with
in N containing F(p) with  , such that
, such that 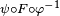 is smooth from
is smooth from 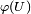 to
to 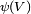 as a function from
as a function from 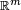 to
to  .
.
Such a map has a first derivative defined on tangent vectors; it gives a fibre-wise linear mapping on the level of tangent bundles.
[edit] Smooth functions between subsets of manifolds
There is a corresponding notion of smooth map for arbitrary subsets of manifolds. If  is a function whose domain and range are subsets of manifolds
is a function whose domain and range are subsets of manifolds  and
and  respectively.
respectively.  is said to be smooth if for all
is said to be smooth if for all  there is an open set
there is an open set  with
with 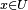 and a smooth function
and a smooth function  such that
such that  for all
for all 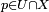 .
.
[edit] See also
[edit] References
|
| This article includes a list of references, related reading or external links, but its sources remain unclear because it lacks inline citations. Please improve this article by introducing more precise citations. (May 2009) |
- ^ a b c Warner (1883), p. 5, Definition 1.2.
- ^ Parametric Curves
- ^ (Bartels, Beatty & Barsky 1987, Ch.13)
- ^ Brian A. Barsky and Tony D. DeRose, "Geometric Continuity of Parametric Curves: Three Equivalent Characterizations," IEEE Computer Graphics and Applications, 9(6), Nov. 1989, pp. 60–68.
-
 This articleincorporates text from a publication now in the public domain:Chisholm, Hugh, ed (1911). Encyclopædia Britannica (11th ed.). Cambridge University Press.
This articleincorporates text from a publication now in the public domain:Chisholm, Hugh, ed (1911). Encyclopædia Britannica (11th ed.). Cambridge University Press. - Guillemin, Pollack. Differential Topology. Prentice-Hall (1974).
- Warner, Frank Wilson (1983). Foundations of differentiable manifolds and Lie groups. Springer. ISBN9780387908946.




 本文介绍了光滑函数的概念,包括其定义、不同阶数的连续性、与解析性的关系以及在数学分析中的应用。此外,还讨论了光滑函数在曲线和曲面几何连续性中的作用。
本文介绍了光滑函数的概念,包括其定义、不同阶数的连续性、与解析性的关系以及在数学分析中的应用。此外,还讨论了光滑函数在曲线和曲面几何连续性中的作用。




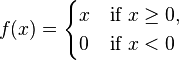
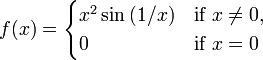
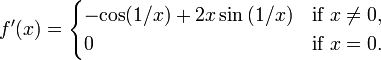

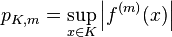



















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








