第十四章 Hash表

 

哈希表基础

问题提出：

https://leetcode-cn.com/problems/first-unique-character-in-a-string/

给定一个字符串，找到它的第一个不重复的字符，并返回它的索引。如果不存在，则返回 -1。

案例:

s = "leetcode"
返回 0.

s = "loveleetcode",
返回 2.

编码实现：

class Solution {
    public int firstUniqChar(String s) {
      int[] freq = new int[26];
        for (int i = 0; i < s.length(); i ++){
            // 把字符映射成数组的下标，数组元素值记录字符的出现的频率
           freq[ s.charAt(i) - 'a'] ++;
        }

        for (int i = 0; i < s.length(); i ++){
            if (freq[ s.charAt(i) - 'a']  == 1){
                return i;
            }
        }
        return -1;  
    }
}

以上我们通过一定的规则：每个字符与一个索引对应（s.charAt(i) - 'a' ）， 将每个字符映射到一个数组（表）元素上：

a---->0

b---->1

c---->2

....

z---->25

依次类推：ch - 'a' = index

把元素转换成索引的函数就称为hash函数，以上的hash 函数就可以写成：f(ch) = ch - 'a',

有些情况下很难保证每个一个“键”通过hash函数的转换对应不同的“索引”， 这时就会产生hash冲突，我们就需要解决hash冲突

hash表充分体现了，算法设计领域的经典思想：空间抽换时间，比如身份号码：140300199106250658, 如果我们有99999999999999999999的空间，我们就可以用0(1)的时间复杂度来完成各项操作。如果我们有1的空间，我们只能用0(n)的时间复杂度来完成各项操作

 

哈希函数的设计

为了避免hash冲突，hash函数的设计是非常重要的，好的hash函数设计的原则是：“键”通过hash函数得到的“索引”分布越均匀越好，对于一些特殊的领域，有特殊领域的hash函数设计方式，甚至有专门的论文讨论如何设计特定领域的hash函数， 这时给出一些通用的hash函数设计方法：

 

进行多项式变形： 

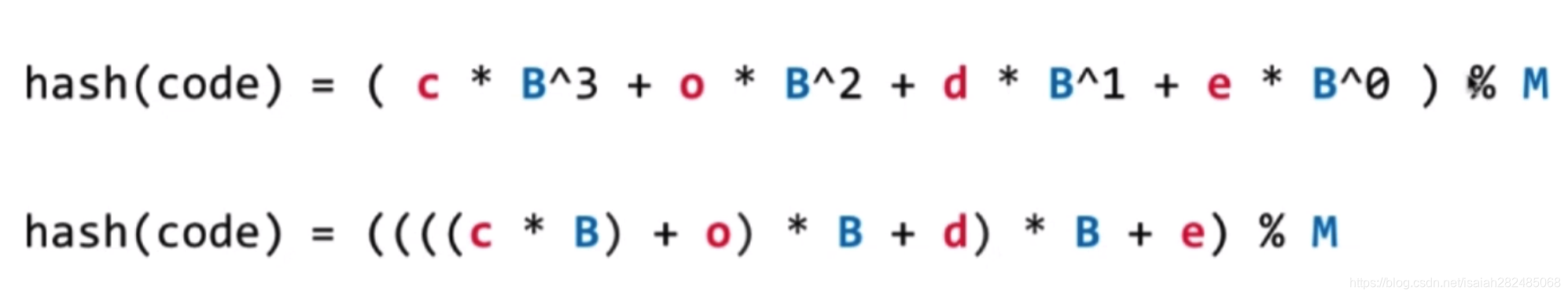
为了防止计算溢出，先进行取模运算： 

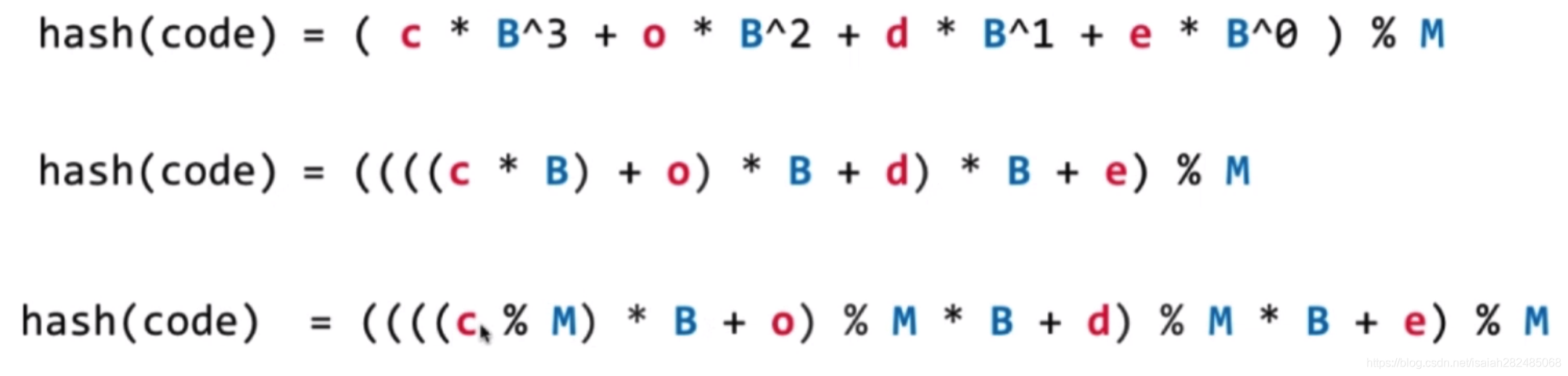
使用代码实现： 

• 整型：
  • 小范围的正整数直接使用
  • 小范围的负整数进行偏移， 如-100~100  -----> 0~200
  • 大整数，如身份证号140300199106250658，通常做法：取模， 如 140300199106250658 到后四位，等同于mod 10000, 需要注意的是，如果取后六位会如何（等同于mod 1000000）？ 140300199106250658 ​​​​​​，这时 25表示的是日，只能取0-31，会生成分布不均匀的情况，另外还有一个总是，没有利用所有信息，这个大整数前面的一些数字也是有意义的，比如表示城市和区域， 所以有些领域需要具体问题具体分析，一个简单的解决办法：模一个索数，这个索数据是多少合适呢？参考网站：https://planetmath.org/goodhashtableprimes 
  • 
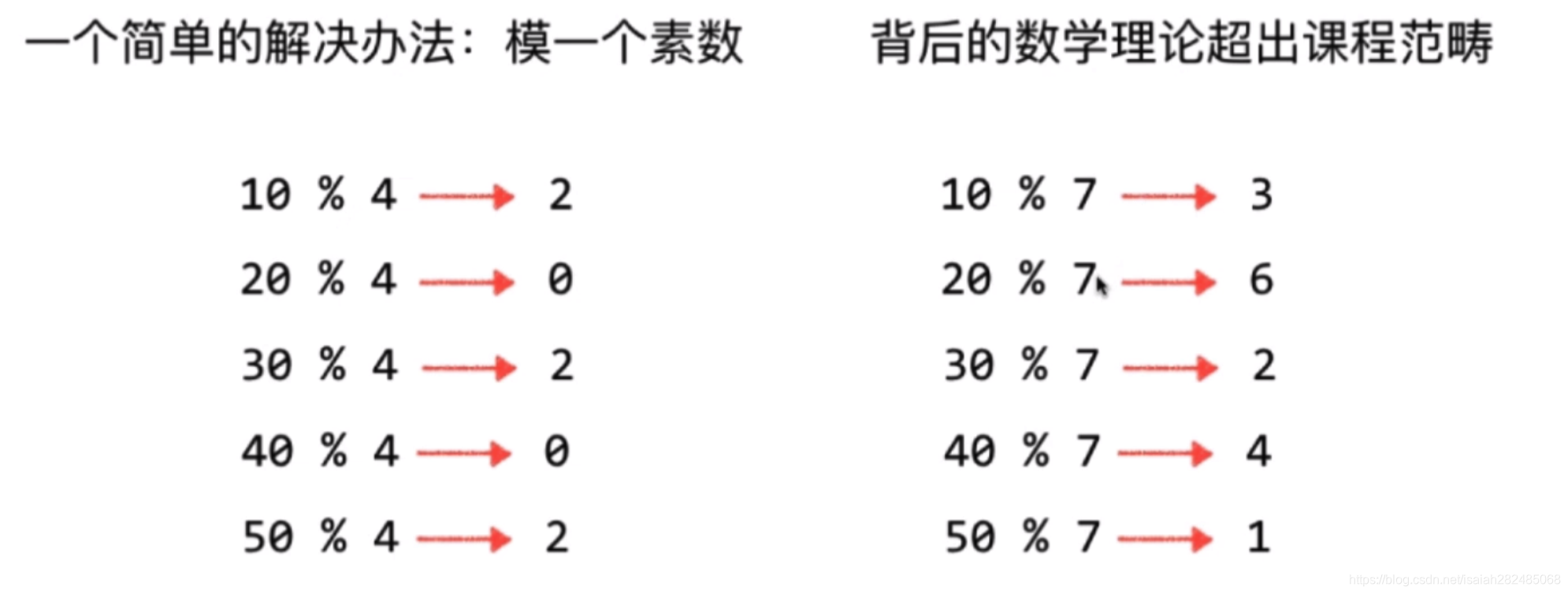
  • 浮点型：在计算机中都是用32位或64位的二进制表示，只不过计算机解析成了浮点数了，所以直接把它当作整数处理
  • 
•  
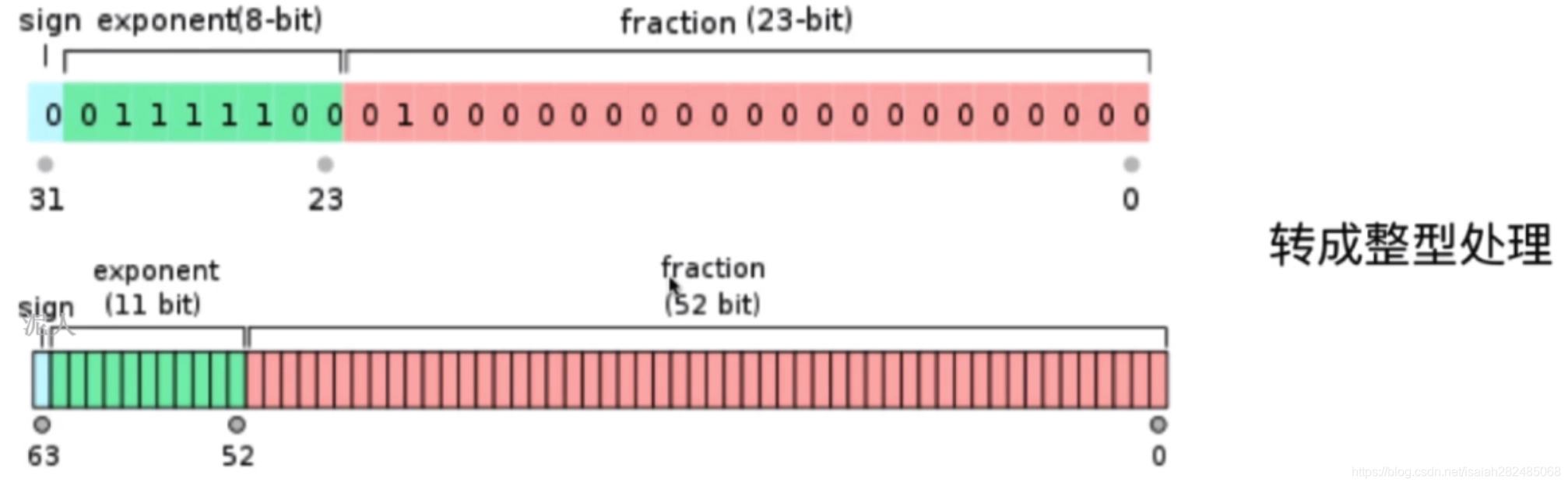
• 字符串型：转成整形处理，字符串的每字符，每一位数字的10进制表示法
• 复合类型：转成整型处理，和字符串处理方式类似
• 

 

hash函数设计原则：

1. 一致性：如果有a==b，则一定有hash(a) == hash(b)
2. 高效性，计算高效简便
3. 均匀性：哈希值均匀分布

思路：把非整型转换成整型处理（并不是唯一方法）

Java中的 hashCode 方法

 

public class Student {
    private int grade;
    private int cls;
    private String firstName;
    private String lastName;

    public Student(int grade, int cls, String firstName, String lastName) {
        this.grade = grade;
        this.cls = cls;
        this.firstName = firstName;
        this.lastName = lastName;
    }

    @Override
    public int hashCode() {
        int B = 31;
        int hash = 0;
        hash = hash * B + grade;
        hash = hash * B + cls;
        hash = hash * B + firstName.toLowerCase().hashCode();
        hash = hash * B + lastName.toLowerCase().hashCode();
        return hash;
    }

    @Override
    public boolean equals(Object obj) {
        if (this == obj){
            return true;
        }
        if (null == obj){
            return false;
        }
        if (this.getClass() != obj.getClass()){
            return false;
        }
        Student other = (Student) obj;
        return this.grade == other.grade && this.cls == other.cls && this.firstName.toLowerCase().equals(other.firstName.toLowerCase()) && this.lastName.toLowerCase().equals(other.lastName.toLowerCase());

    }
}

public class Test {

    public static void main(String[] args){
        int a = 50;
        int b = -50;
        System.out.println(((Integer)a).hashCode());        // 50
        System.out.println(((Integer)b).hashCode());        // -50
        double c =3.14159;
        System.out.println(((Double)c).hashCode());         // -1340954729
        String d = "imooc";
        System.out.println(d.hashCode());                   // 100327135

        // Java默认的hashCode是由Object类实现，返回的是对象的hash地址，我们应该根据业务实现自己的hashCode方法
        Student student = new Student(1, 2, "Haijun", "Liu");    // 688512230
        System.out.println(student.hashCode());

        HashSet<Student> hashSet = new HashSet<>();
        hashSet.add(student);

        HashMap<Student, Integer> hashMap = new HashMap();
        hashMap.put(student, 99);
    }

}

注意点：

1. 在使用HashSet和HastMap这样的Hash表时，一定要重写类中的hashCode()方法。
2. 在使用HashSet和HastMap在产生hash冲突时，同样要比较两个对象是否相等，所以要重写equals()方法

 

解决Hash冲突几种方式

 

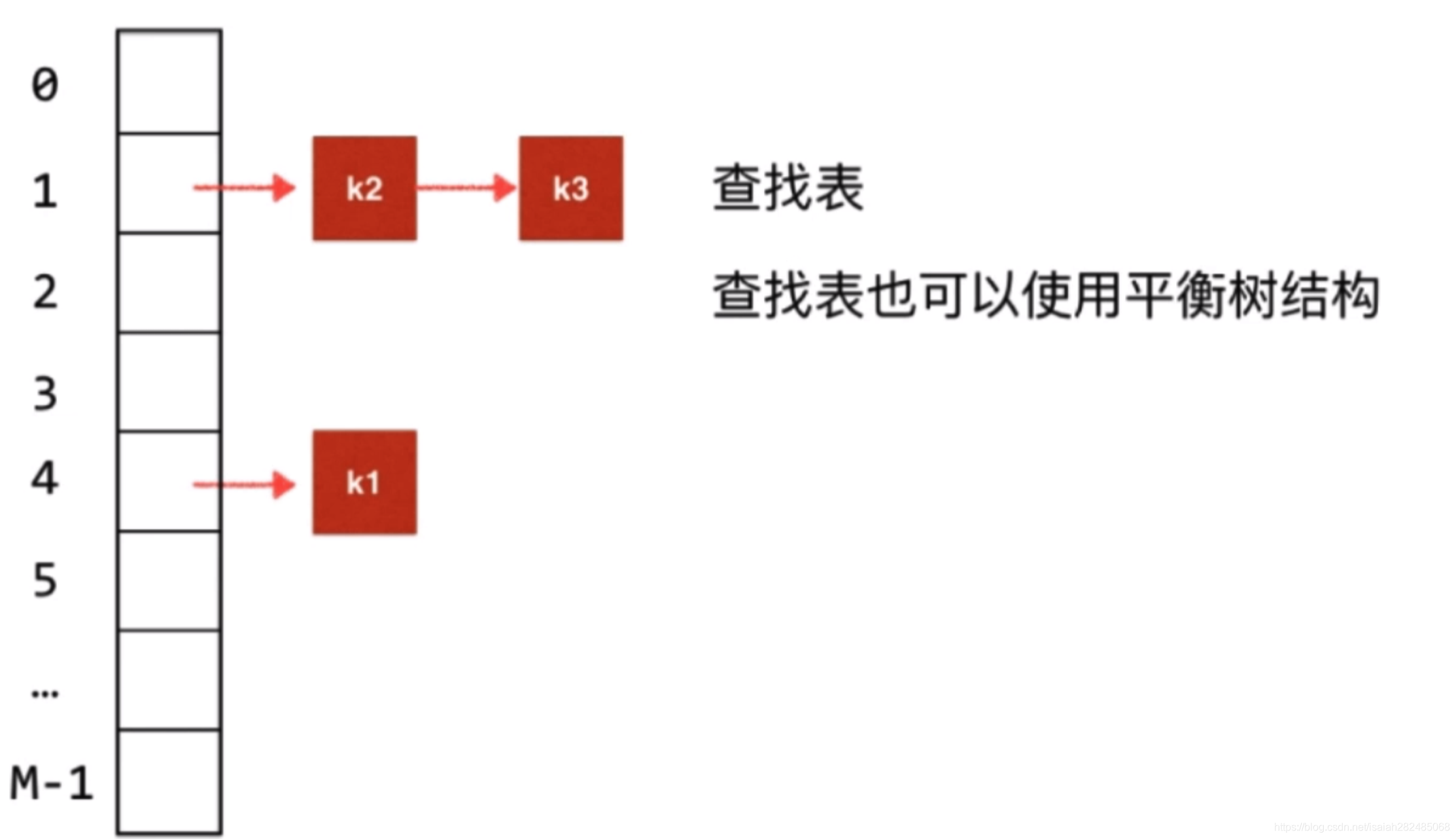
链地址法

在之前我们了解Hash表，本身就是一个数组，hash表中每个位置，存储一个链表，当发生hash冲突时，将元素插入到这个链表中， 其实在Java语言中HashMap/HashSet就是使用链地址法解决hash冲突的

 

取除负号方法：一个整数与&0x7ffffffff进行与运算， 其实就是一个整数31个1这样一个二进制进行与运算，这样的结果符号位一定是0， 也就是让它变成一个正数

在java8之前，Hash表的每一个位置对应一个链表，在java8开始，当hash冲突达到一定程序时链表会转换成红黑树

开放地址法

相对开放地址法来说，链地址法是种封闭地址，它只能包含hash值等于这个索引对应的元素，在开放地址法hash表的每个一个地址，所有hash值的元素都有机会进来，第一个地址对所有元素开放，都可以存放进来。对于开放地址法来说，如果有冲突，可以向后移动一个位置进行存放，不存在冲突

 

线性探测并不是太理想，有些情况下一直探测效率比较低，遭遇的冲突比较多，进而还有平方探测法进行改进：

当然平方探测法还是存在一定的规律性，还有另外一种方法二次哈希法

 

Hash表的容量有限，当元素占满到一定程序时，我们也应该要扩容，通常有一个指标叫负载因子

 

再哈希法Rehashing

当我们使用一个hash函数产生的索引冲突后，我们使用另外一个hash函数找相应的索引

Coalesced Hashing

综合了Seprate Chaining 和 Open Addressing这两种方法

 

实现自己的Hash表

 

public class HashTable <K, V>{

    private TreeMap<K, V>[] hashTable;
    private int M;
    private int size;

    public HashTable(int M){
        this.M = M;
        this.size = 0;
        this.hashTable = new TreeMap[M];
        for (int i = 0; i < M; i++){
            hashTable[i] = new TreeMap<>();
        }
    }

    public HashTable(){
        this(97);
    }

    private int hash(K key){
        return key.hashCode() & 0x7fffffff % M;
    }

    public int getSize(){
        return this.size;
    }

    public void add(K key, V value){
        TreeMap<K, V> map = hashTable[hash(key)];
        if (map.containsKey(key)){
            map.put(key,value);
        }else{
            map.put(key, value);
            this.size ++;
        }
    }

    public V remove(K key){
        TreeMap<K, V> map = hashTable[hash(key)];
        V ret = null;
        if (map.containsKey(key)){
            ret = map.remove(key);
            this.size --;
        }
        return null;
    }

    public void set(K key, V value){
        TreeMap<K, V> map = hashTable[hash(key)];
        if (!map.containsKey(key)){
            throw new IllegalArgumentException(key + " doesn't exist!");
        }
        map.put(key, value);
    }

    public boolean contains(K key){
        return this.hashTable[hash(key)].containsKey(key);
    }

    public V get(K key){
        TreeMap<K, V> map = hashTable[hash(key)];
        return map.get(key);
    }
}