Python 与神奇的数学之龙形曲线

        龙形曲线（Dragon Curve），又叫分形龙，是一类自相似碎形曲线的统称，因形似龙的蜿蜒盘曲而得名。

        如果您玩过折纸游戏，可以如下种简单的方式生成分形龙：将一条细长的纸带对折，然后将对折后的纸带再对折，又再对折，如此重复……然后依折线垂直展开，就生成了分形龙的图形。

        龙形曲线如同科赫曲线，亦为比较典型的分形图形，具有不断迭代和递归的特点。由此，我们可以定义该曲线的函数为：

def dragon(curve, n):
    if n == 0:
        return
    
    for i in curve:    #起始位置
        if i == 'H':    #水平
            dragon('HLVF', n-1)
        elif i == 'V':    #垂直
            dragon('FHRV', n-1)
        else:
            if i == 'F':
                fd(60)
            elif i == 'L':
                lt(90)
            elif i == 'R':
                rt(90)

        由此，迭代形成的图形：

        2 次迭代，顶点数 3

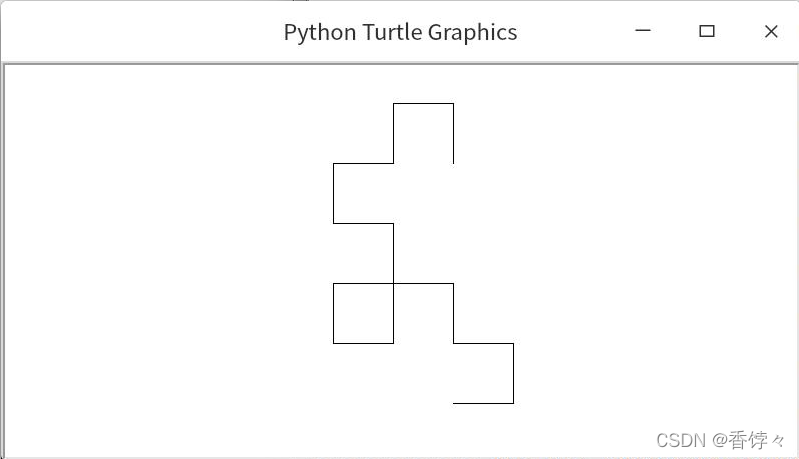
        4 次迭代， 顶点数 15

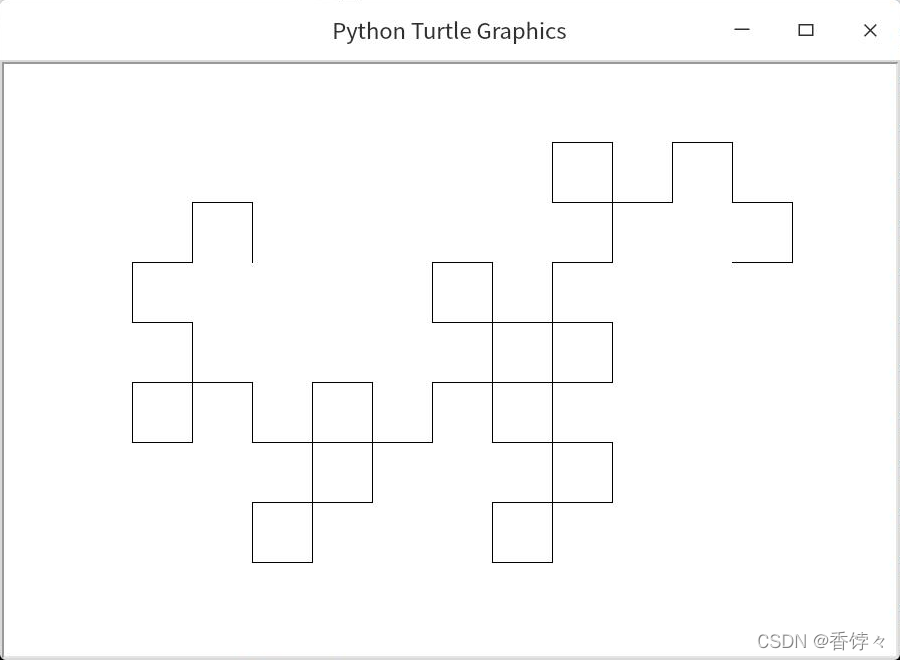
         6 次迭代， 顶点数 63

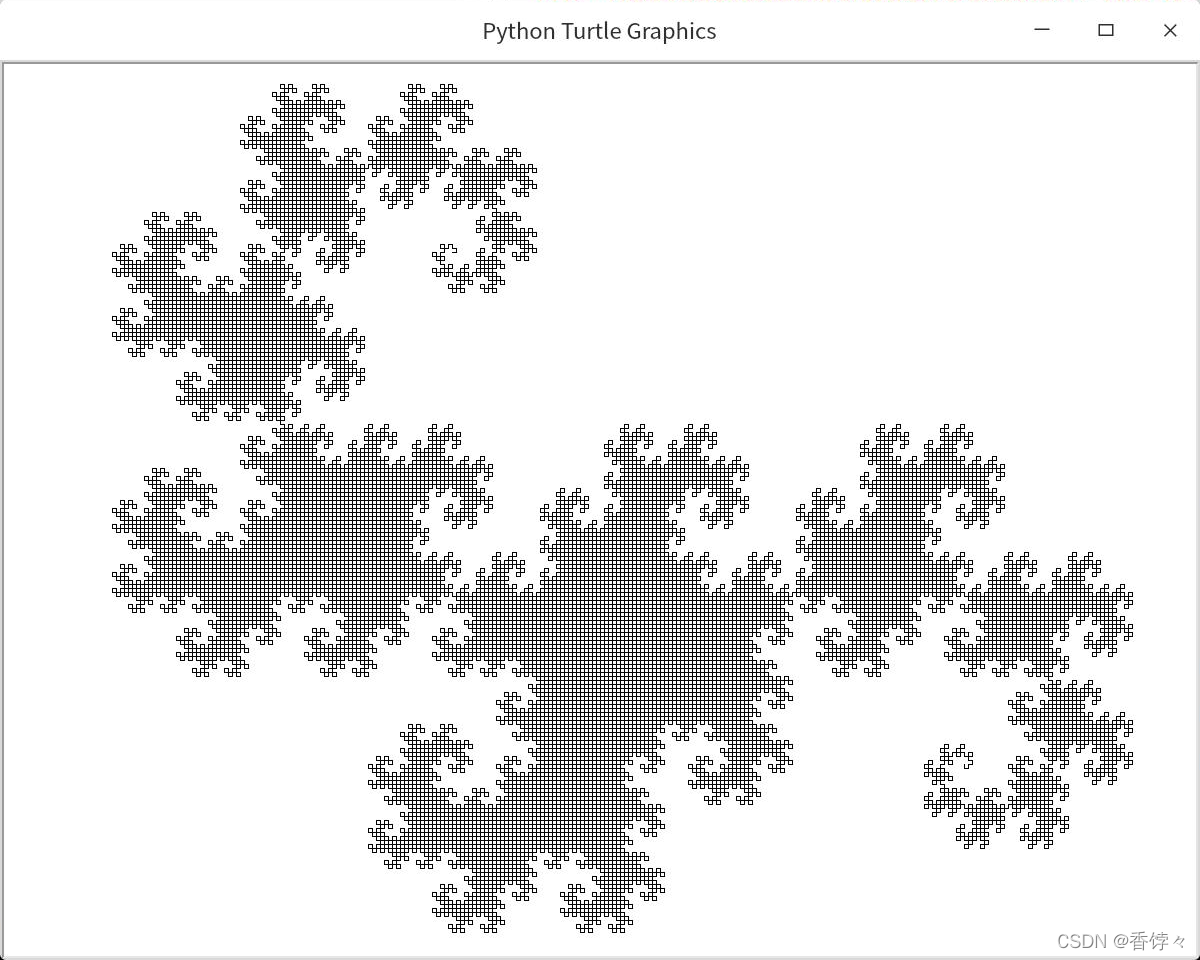
         15 次迭代， 顶点数 32767。其完整代码为：

from turtle import *
 
def dragon(curve, n):
    if n == 0:
        return
    
    for i in curve:
        if i == 'H':
            dragon('HLVF', n-1)
        elif i == 'V':
            dragon('FHRV', n-1)
        else:
            if i == 'F':
                fd(4)
            elif i == 'L':
                lt(90)
            elif i == 'R':
                rt(90)
 
def main():
    curve = 'V'
    setup(1200, 900)
    up()
    goto(-150,260)
    down()
    seth(0)
    speed(0)
    dragon(curve, 16)
    ht()
 
main()

        当然，您也可以利用 n = eval(input()) 输入任何您想要的迭代次数，只要您感兴趣。