基于代理感知的传感器网络优化

利用代理感知实现大规模传感器网络的高效监测

1 引言

将物理和社会基础设施持续转变为智能的网络‐物理系统，需要大规模部署物联网设备，每个设备配备一种或多种适当类型的传感器。这些应用的一些示例包括电力、水和食品分配的智能管理，以及交通系统、医疗设施和污水/废物处理等。一座智慧城市将包含所有这些协同工作的系统，从而形成更加复杂的感知模态集合。此类网络可能由许多不同的子网络组成，这些子网络或许由不同的供应商部署，甚至由不同的实体控制。

新兴的边缘计算范式[1]通过其三层架构支持这些使用模式，其中每个子网络由一个边缘控制器管理，该边缘控制器还提供实时数据分析和控制能力，并提供通往远程云（第三层）的路径，以实现长期数据存储和离线的全系统数据分析。一个边缘控制器以及单个控制器能够管理的子网络规模取决于许多因素，例如子网络的物理跨度、通信/计算负载以及成本和部署问题。在许多应用中，实时分析需求可能很小，因此边缘控制器可以通过蜂窝网络或卫星等合适技术连接到多个指定节点，从而服务一个较大的子网络。我们因此假设子网络本身使用不同的技术（例如蓝牙、无线局域网或802.11ah/af），这些技术可以形成自组织网络，将数据传输至连接边缘控制器的指定节点。

在具有多种感知模态的大型物联网设备网络中，考虑“代理感知”这一现象具有重要意义——即通过某个传感器推断出其并未直接测量的信号信息。代理感知是一种广为人知的现象，出现在多种场景中，主要原因至少有以下三点。第一个原因是（未测量的）属性对已测量属性的影响。例如，市政饮用水中的大多数污染物可以通过常见的指标进行检测，如pH值、氧化还原电位（ORP）以及氯含量的变化。其他例子包括公共场所的人口密度与噪声水平之间的相关性，以及生鲜食品包装内部的平均温度与腐败症状之间的关联。第二个原因是传感器之间的空间相关性。例如，相邻房间内的两个温度传感器报告的温度值可能几乎相同，或其温差保持基本恒定，因此可以降低测量频率。类似地，某一区域的交通密度或污染情况也可用于推断邻近区域的情况。第三个原因是两个区域之间的情境相似性，这也允许进行更稀疏的测量。例如，在相似冷却条件下运输的同类食品，无论其物理位置如何，都不需要对其质量劣化情况进行密集监测。

尽管单个传感器仅感知一种属性，但通常会在一个物联网设备内集成多个异构传感器（此外还包括合适的无线通信模块）。包括智能手机在内的大多数物联网设备都搭载了越来越多的传感器。例如，传统生鲜食品供应链仅依赖温度测量，而较新的传感器还可检测挥发性有机化合物（VOCs），并将其与质量劣化相关联[2]。类似地，植物健康传感器可测量温度、湿度、土壤pH值等。由于大多数物联网设备功耗或尺寸受限，其节能运行至关重要。此外，在许多应用中，监测需求集中在某些兴趣点（PoIs）周围。通常，兴趣点会持续变化，但其变化速度远慢于感知频率。利用代理感知对于优化与兴趣点相关的数据采集非常有帮助。特别是，需要动态调整感知频率，以优化感知任务的能效和鲁棒性。

1.1 我们的贡献

鉴于由子网络和自组织路由组成的大型网络的假设，本文的主要贡献如下：

• 我们分析了分布式采样率自适应方案，以根据单个传感器的可用能量、网络参与度和相关性，将数据采集任务在它们之间进行分配。我们提出了两种基于分解的分布式解决方案，分别使用次梯度法和Nesterov梯度下降算法[3]来调整多跳无线传感器网络中单个传感器的采样率。
• 通过大量仿真，我们表明次梯度法和涅斯捷罗夫方法在采样率收敛以及消息交换方面都需要大量的迭代次数。鉴于此，我们提出了两种混合方案，并通过大量仿真表明，这些方案在大约10到15次迭代内即可收敛。我们认为，此处考虑的基于兴趣点的监测比节点独立的采样率自适应更适用于大规模传感器网络的许多实际应用[4]。

本文扩展了我们先前的会议论文[5]，在多跳无线传感器网络环境中，对多传感器代理感知框架进行了实质性改进。我们还全面评估了该框架在多个实际应用场景中的适用性，包括（1）变电站监控环境，其中设备配备有振动、气体和温度传感器；（2）灾害管理场景，其中设备配备有摄像头、麦克风和加速度传感器；以及（3）管道监控场景，其中设备配备有氯、氧化还原电位和pH传感器。

1.2 文章结构

本文其余部分组织如下。第2节讨论了若干可从本文所述方法中受益的协同感知应用。本节还包括一些基本定义和符号说明。第3节介绍了优化模型以及所采用的分布式方法，并分析了它们的优缺点。第4节描述了两种可扩展的替代方案，以加快速率自适应过程。第5节展示了大量仿真结果。相关提案和相关内容的讨论总结于第6节。我们在第7节对全文进行总结。

2 协同速率自适应

2.1 潜在应用领域

一组异构传感器通过协同感知和速率自适应对特定兴趣点进行最优监测，适用于多种感知应用，以下列举其中一些。

灾害监测。 各种形式的灾害，例如地震、飓风和电磁风暴，可能会严重破坏蜂窝通信基础设施，因此可极大地受益于涉及智能手机的自组织网络，尤其是部署的应急通信基础设施[6–8]。此处的监测需求包括与特定兴趣点（PoI）处损害评估和救援相关的图像、声音和运动信息，而这些地点的情况可能尚不明确。例如，加速度计通常与速度地震仪结合使用，用于测量和记录地面运动或振动的程度。音频样本也可用于追踪建筑物倒塌的声音。视频和图像可用于构建地震造成损害的空间视图。在此示例中，这三种传感器均测量了同一地面运动现象的某些方面。这种空间和跨传感器相关性可用于使传感器循环启停，以调节其节能性。所部署的解决方案必须考虑到智能手机有限的电池寿命，以及各种传感器采集数据之间存在的相关性。

城市水污染物检测。 供水系统（WDS）中潜在污染物的数量相当多[9, 10]，因此为每种污染物部署对应的单个传感器成本高昂且不切实际。一种更可行的方案是使用测量指示性或代理参数的传感器，以检测异常水质，从而进行可能的污染评估[9]。游离氯是对污染最敏感的指标，其在浓度通常比致死浓度低一到两个数量级时，便已显著偏离基线值。水中的总有机碳（TOC）是检测多种有机化合物存在的另一个重要代理参数。电导率也被观察到对某些无机污染物和金属有轻微响应。氧化还原电位（ORP）通常表现类似用于余氯，可用于证实观察到的余氯变化。pH值对于了解水体的水化学性质至关重要。浊度或水体浑浊度是污染的一种不稳定且不可靠的主要指标。

这种多传感器环境可以从所提出的协作和集体感知框架中受益。由于水中污染物数量众多，检测通常由一组有限的“代理传感器”完成，例如氯、有机碳、电导率、pH值和浊度[11]。有限的电池寿命和相关性在此应用中同样重要，而在某些潜在污染源处的监测尤为关键。

森林监测。 远程森林监测应用包括栖息地、天气状况以及突发的森林火灾，同时还需要检测破坏森林财产的偷猎者。栖息地监测可以通过在感兴趣区域部署多个摄像头传感器来实现，而天气状况则可通过不同的温度和湿度传感器进行监测。然而，森林火灾监测极为关键，以便在造成重大破坏之前采取主动措施。在美国，每年通常会发生60,000至80,000起野火，烧毁300万至1000万英亩的土地[12, 13]。可在易发生野火的区域部署一些配备温度和烟雾检测传感器的无线设备。除了火灾检测外，非法捕杀野生动物或破坏野生植物对野生动物保护与维护至关重要。特别是在非洲和亚洲，由于象牙和黑犀牛角的价格上涨及需求增加，偷猎问题正变得日益严重[14]。非洲黑犀牛属于极危物种，其种群数量在过去三代犀牛期间已减少了80%[15]。偷猎者检测传感器包括视频、音频以及埋设于地下的负荷传感器。热成像技术在探测偷猎者方面十分有效，尤其是在夜间。此类监测活动需要在不同位置布置多种类型的传感器，但如何协同检测并上报所需参数以最大化整体检测覆盖范围仍是一项挑战。

滑坡监测。 滑坡是一种由陡坡角度、坡脚侵蚀和饱和土壤引起的短暂性破坏性现象[16]。在印度，滑坡造成的年度损失平均达4亿美元。滑坡的关键特征包括土壤湿度、孔隙压力、土壤振动和温度。设备需要埋入地下以采集这些样本并将其报告给中央站。在强降雨期间，土壤湿度传感器可提供潜在滑坡的早期预警。随着降雨增加，雨水在土壤孔隙中积聚，产生负压，导致土壤强度减弱，这一现象可通过振弦式孔隙水压力计或应变计型孔隙水压力计进行测量[16]。滑坡引起的振动使用地震检波器进行测量，而土壤温度则可通过温度传感器测量以检测显著异常。由于监测设备需要埋设，其电池寿命至关重要。此外，许多传感器读数之间存在相关性，可利用这些相关性实现能量自适应。因此，多传感器协同代理感知也可直接应用于该场景。

变电站监控。 配电变电站包含多个关键组件，例如必须持续监测的断路器和变压器，以减少发生昂贵且造成干扰的停电的可能性。由于变电站设备和基础设施日益老化，这一问题正变得越来越突出。[17]变电站和配电中心使用断路器将电路或设备接入或脱离整个系统。这些设备通常充有油或SF6气体。在油浸式断路器中，油在开关动作时起到冷却和防止电弧的作用。此类变电站监控应用需要对油温、粘度、泄漏等进行连续监测，以便及时检测并报告任何异常情况。同时，断路器

2.2 网络模型

接下来，我们描述我们方案的网络模型。我们假设一些无线设备配备了多传感器，用于感知不同的物理参数，并将这些参数报告给一个集中位置。为了清晰起见，我们将这些独立的无线设备定义为节点，而使用“传感器”一词来描述附着在该节点上的各种传感器。例如，智能手机可以被视为一个节点，其上配备了加速度计、温度和音频传感器等各种传感器。

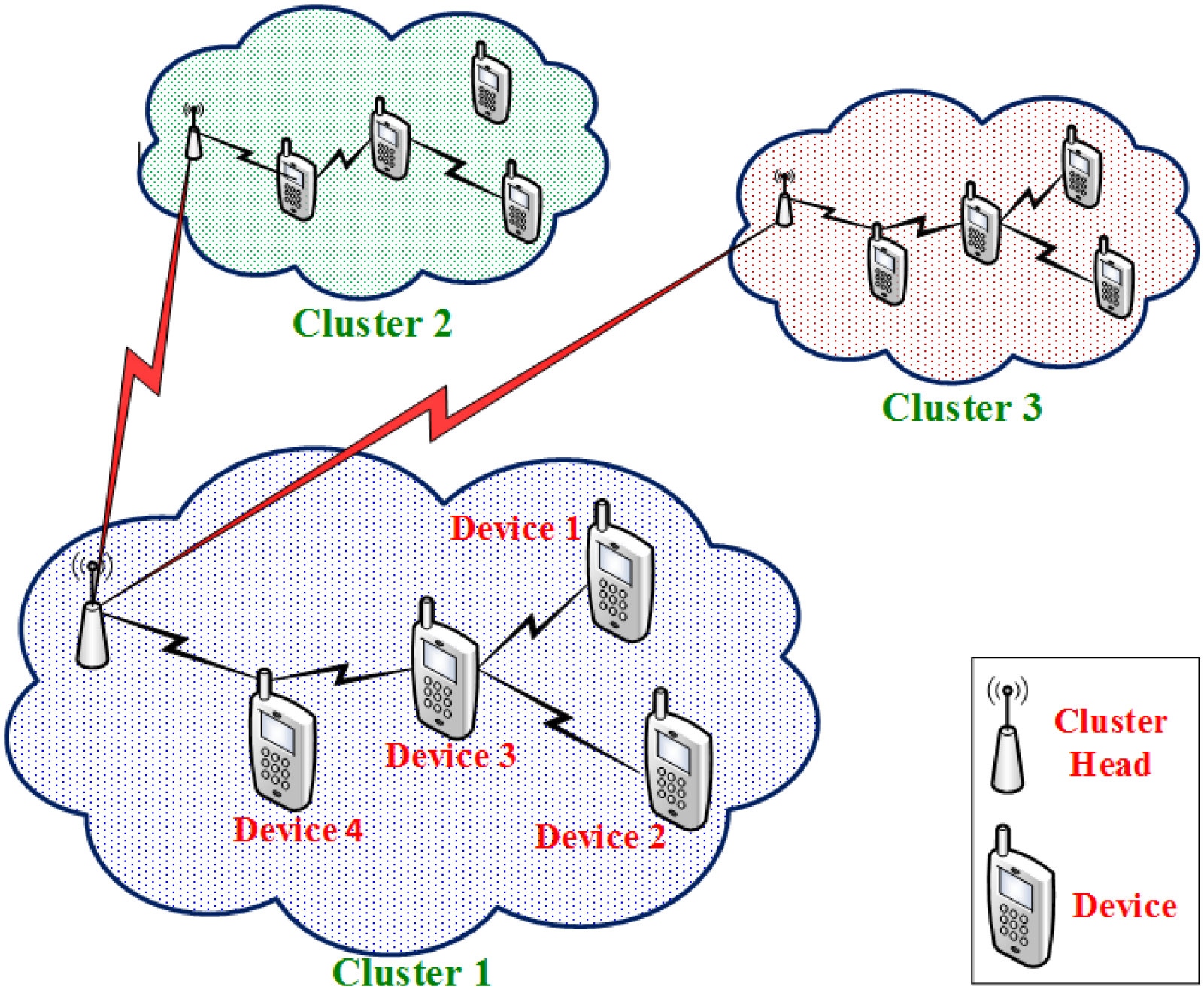
我们假设整个网络由若干个互不相交的簇组成，每个簇都有其自己的簇头（CH）。在边缘计算的术语中，这些簇头可被视为边缘控制器，每个边缘控制器管理一个完整的物联网设备子网络。这种划分可能是自然的——由不同的物理/逻辑簇决定，可能由不同的实体进行管理。这种划分也可能是人为的，例如将一个大型网络划分为多个簇，以实现本文所讨论的自适应目的。无论哪种情况，每个簇中的节点都会将其流量转发给其簇头。为简化起见，我们假设簇头之间可以直接通信，并且不受能量限制。整体网络模型如图1所示。此类网络模型适用于许多无线传感器网络应用场景，如第2.1节所述。例如，在灾害管理场景中，可能在较大的地理区域部署一些接入点（AC；汇聚点），每个接入点形成一个包含若干节点的簇。这些接入点配备有蜂窝或卫星天线，因此能够相互通信。节点通过广播周期性信标来交换各种控制参数。节点发现其邻居，并使用收集树协议（CTP）构建到其簇头的路由。

为了评估路由的质量，我们使用路径度量，该度量是通过将其各链路上的预期传输次数（ETX）相加得到的，这与CTP中采用的原则相同。链路的ETX是指成功在该链路上传输一个数据包所需的预期传输尝试次数。在CTP中，路径选择基于最大化路径质量度量或最小化路径ETX（即路径上各链路ETX之和）来进行。我们还将节点的min‐ETX定义为通向其簇头（CH）的最佳质量路由的路径ETX。

在我们的模型中，我们将一个节点的潜在父节点(PPs)定义为一组邻居节点，这些邻居节点的 ETX小于该节点的ETX。除了ETX之外，簇头节点(CHs)还在其信标消息中广播一些需要节点监测的兴趣点(PoIs)。在灾害管理应用中，这些点可能是受灾害严重破坏的区域，或是灾害管理部门尚未掌握其受损程度的区域。在水污染物检测场景中，这些点是供水系统(WDS)希望监测污染物浓度和水质的地点。这些兴趣点(PoIs)通常会随时间演变，但由于这一过程非常缓慢，因此不会影响此处讨论的问题。这些兴趣点(PoIs)将用于调整节点的采样率，具体方法将在后文提及。

我们假设节点之间没有时间同步，并采用一些低功耗监听（LPL）[18]机制，例如 X‐Mac原理[19]来节省能量。在X‐Mac中，发送方会发送多个脉冲数据包，这些脉冲数据包覆盖整个休眠‐唤醒周期的长度，以确保接收节点无论何时唤醒都能检测到信号。脉冲数据包中包含接收方的地址，因此其他邻居节点或旁听者在听到针对其他节点的脉冲信号时，可以避免保持其无线电设备开启。当接收方收到一个脉冲数据包时，它会立即发送确认信号，随后发送方立刻发送数据包。这种机制减少了接收和旁听过程中的持续时间和功耗。

因此，能耗的主要来源是感知不同参数并将这些参数通过多跳方式转发给簇头节点。

我们假设需要由节点监测的POIs有 E个。除了POIs外，簇头节点还会广播围绕每个POI更需重点监测的区域，该区域表示为以第k个POI为中心、半径为 ϱ k的范围。此外，我们假设整个区域内的节点数量为 S个，每个节点所拥有的不同类型传感器的数量为 T个。假设ptk i表示第 i个节点中类型为t的传感器覆盖第k个兴趣点的权重。如果一个节点位于某个POI直接通信半径范围内，则其权重为1；若超出该半径，权重则随距离呈指数下降。因此，

$$ p_{tk}^i(d_k^i)= \begin{cases} 1 & d_k^i < \varrho_k \ e^{-\eta_t (d_k^i - \varrho_k)} & d_k^i > \varrho_k \end{cases}, $$

其中dik表示第i个节点与第k个兴趣点之间的距离。 η t是超过 ϱ k的衰减率，该衰减率因不同传感器而异。我们假设节点已定位，并利用其位置信息来测量它们与兴趣点之间的距离。

2.3 定义与符号

我们现在简要定义一些与后续推导相关的符号、术语和基础知识。

矩阵范数。 我们定义一个m × n矩阵A的l1, l2,和l∞范数分别为 ||A||1、 ||A||2和 ||A||∞。 ||A||1= max1≤j ≤n∑ m i=1 |aij |，即矩阵A的最大绝对列和。 ||A||∞= max1≤i≤m∑ n j=1 |aij |，即矩阵 A的最大绝对行和。l2范数与矩阵ATA的谱半径相关，关系如下：

$$ \rho(A^T .A)= ||A|| 2^2 \leq ||A||_1.||A|| \infty, $$

其中 ρ(A^T.A) 是 AT.A 的谱半径。

利普希茨连续性。 接下来我们定义一个函数的利普希茨连续性，它用于衡量函数值的变化相对于自变量x ∈ I 的变化，针对一般函数f(x)。如果x1和x2是两个数，则 |x2 −x1| 是 输入的变化，而 |f(x2) −f(x1)| 是相应的输出变化。我们说f是利普希茨连续的，其利普希茨常数L如果存在一个正数常量L使得

$$ |f(x1) − f(x2)| \leq L.|x1 − x2| \quad \forall x1, x2 \in I. $$

请注意，Lipschitz常数是对函数f变化程度的上界估计，而实际变化可能远小于该常数所表明的值。

强凸函数。 一个凸函数 f 是 σ‐强凸的，如果

$$ f(y) \leq f(x)+ \nabla f(x)^T.(y− x)+ \frac{\sigma}{2}||y− x||_2^2 \quad \forall x, y \in \text{dom}(f). $$

如果f是二次可微的，则m‐强凸性等价于

$$ \nabla^2f(x) \succeq \sigma.I \quad \forall x \in \text{dom}(f), $$

其中I是单位矩阵。

3 自适应采样与传输

在多传感器协作无线传感器网络中，节点需要根据其电池电量调整单个传感器的传输与传感速率，以便根据各自的功率预算累积地分担数据采样和转发任务。

3.1 基本问题建模

我们现在提出基本的自适应采样和传输速率自适应方案，旨在最大化兴趣点的整体覆盖范围，并确保节点不会耗尽电池电量。问题建模中使用的符号列于表1中。我们通过考虑两个因素来定义节点t对节点i的感知效用：

• 感知速率 $r_{ti}$：随着$ r_{ti} $的增加，采样点数量增加，效用也随之增加。
• 它们对应的权重 $w_{tki}$ 在覆盖兴趣点时：$ w_{tki} $是两个因素的乘积：（1）$ p_{tki} $，其取决于节点距离兴趣点的远近；（2）传感器之间的相对权重$ a_{tki} $（例如，图像可能比音频样本更重要等）。如果一个传感器的整体权重更高，则其对效用函数的贡献也更大。在不失一般性的前提下，我们假设$ w_{tki} \leq 1 $。本质上，$ w_{tki} $将代理感知的概念引入模型中——例如，多个传感器可以以一定的权重感知同一兴趣点。

考虑到上述两个因素，第k个兴趣点被t型传感器监测的有效速率为 $ \xi_{tk}=\sum_{i=1}^{S} w_{tki} .r_{ti} $。

因此，通过将第k个兴趣点由t传感器报告的效用建模为$ U_k(\sum_{t=1}^{T} \xi_{tk}) = \log(\sum_{t=1}^{T} \xi_{tk}) $，来确保公平事件报告能力。我们的目标是在满足单个节点能量预算的前提下，最大化整体事件监控能力（即$\sum_{k=1}^{E} U_k(\sum_{t=1}^{T} \xi_{tk})$）。因此，整个优化问题可表述如下：

Original Problem(OP):

$$
\text{Maximize} \sum_{k=1}^{E} \log\left( \sum_{i=1}^{S} \sum_{t=1}^{T} w_{tki} .r_{ti} \right)
$$

$$
\text{subject to} \sum_{t} r_{ti}(e_t + c_t)+\sum_{t} \sum_{j \in D_i} \alpha_{ji} .r_{tj}.c_t \leq E_i \quad \forall i
$$

$$
R_m \leq r_{ti} \leq R_M \quad \forall i,\forall j,\forall t.
$$

我们假设 $ \alpha_{ji} $是节点j经过其PPi的流量比例。稍后我们将证明，在我们的方案中，每个节点仅需要其PPs的 $ \alpha_{ji} $。因此，节点j可以根据其PPs的数量及其路由成本来近似计算其PPi的$ \alpha_{ji} $。第一个约束是能量预算约束，表示用于感知和传输所消耗的能量小于某个阈值 Ei。Rm和RM分别是节点传感器的最小和最大采样率，它们根据（1）节点的剩余电池电量、（2）传感器的可用性以及（3）方案的数据收集需求进行调整。该模型通过引入项$ w_{tki} $自动考虑了邻近节点之间的空间相关性影响。此外，通过将传感器的累积效应纳入对数函数中，模型还考虑了传感器间的固有相关性。

优化问题（6）是一个凸优化问题，因此可以使用标准方法轻松求解。然而，这种解决方案需要将前述公式化中涉及的所有信息集中到一个中心节点来进行优化，这在大型网络中可能难以实现，原因包括：难以在中心点获取一致的全局状态；不同方拥有或操作的子网络之间的信息可见性/传输限制；由于无线信道效应（例如衰落、干扰）导致的路径延迟增加；以及由于中间节点发生故障、耗尽的电池、阴影效应和攻击等原因，导致信息对中心节点不可用的可能性更高。

因此，我们的目标是采用一种迭代的、分布式方法来解决此问题。请注意，此处提到的所有问题在采用分布式方法时同样可能出现，但它们将随着节点之间所需交互量的减少以及信息传输路径长度的缩短，问题的严重性会降低。然而，在从完全分布式到完全集中式的所有情况下，信息交换算法都必须应对所需信息不可用的问题。这包括以下方面：(1) 超时机制，以限制算法等待接收信息的时间；(2) 基于先前值的时间序列预测技术对缺失信息进行近似估计；(3) 处理过期信息（例如在超时后到达的消息）。由于这些技术已广为人知并广泛应用，因此我们不再进一步讨论。

3.2 分布式问题建模

以分布式方式求解该问题带来两个关键挑战。首先，尽管对数是关于变量$ w_{tki}.r_{ti} $的严格凹函数，但由于项$\sum_{i=1}^{S}\sum_{t=1}^{T} w_{tki}.r_{ti}$的存在，目标函数是非严格凹函数。其次，该函数关于每个节点i是不可分离的。第一个问题可以通过在目标函数中添加一个增广变量[20, 21]使其变为严格凹函数来解决。然而，新的严格凹函数关于i仍然是不可分离的。为应对这一问题，我们采用类似于Vo等人的方案[22]，如下所述。

由于对数是对数函数，利用詹森不等式可得

$$
\log\left( \sum_{i=1}^{S} \sum_{t=1}^{T} w_{tki}.r_{ti} \right) \geq \sum_{i=1}^{S} \sum_{t=1}^{T} \theta_{tki} \log\left( \frac{w_{tki}.r_{ti}}{\theta_{tki}} \right) \quad \forall i,\forall t,\forall k,
$$

where

$$
\theta_{tki}= \frac{w_{tki}.r_{ti}}{\sum_{i=1}^{S}\sum_{t=1}^{T} w_{tki}.r_{ti}} \quad \forall i,\forall t,\forall k.
$$

使用修改后的目标函数，新的优化问题MOP建模如下：

改进的优化问题（MOP）：

$$
\text{Maximize } U= \sum_{k=1}^{E} \sum_{i=1}^{S} \sum_{t=1}^{T} \theta_{tki} \log\left( \frac{w_{tki} .r_{ti}}{\theta_{tki}} \right)
$$

$$
\text{subject to} \sum_{t} r_{ti}(e_t + c_t)+\sum_{t} \sum_{j \in D_i} \alpha_{ji}.r_{tj} .c_t \leq E_i \quad \forall i
$$

$$
R_m \leq r_{ti} \leq R_M \quad \forall i,\forall j,\forall t.
$$

接下来，我们提出两种分布式方案来解决问题（8）。第一种是基于次梯度的分布式解法，而另一种则基于涅斯捷罗夫方法[3]。我们将说明，当完全以分布式方式应用时，这两种方案均表现不佳；然而，它们为第 4 节讨论的部分分布式方案奠定了基础。

3.3 一种基于次梯度的分布式方案

MOP 在给定 $ \theta_{tki} $ 的情况下关于i严格凹且可分离。因此，我们现在可以像之前解决效用最大化问题[20,23, 24]一样，通过对偶分解进行分布式求解。我们首先假设

$$
\Lambda_{ti} = \sum_{k=1}^{E} \theta_{tki} \log\left( \frac{w_{tki} .r_{ti}}{\theta_{tki}} \right) \quad \text{and} \quad \Theta_{ti} = r_{ti}(e_t + c_t).
$$

然后可以定义拉格朗日函数为。

$$
L(r,\nu)= \sum_{i=1}^{S} \sum_{t=1}^{T} \Lambda_{ti} - \sum_{i=1}^{S} \nu_i\left(\sum_t \Theta_{ti}+\sum_t \sum_{j \in D_i} \alpha_{ji}.r_{tj} .c_t - E_i\right)
$$

对偶问题的目标函数可以写成。

$$
D(\nu)= \text{Max } L(r,\nu)= \text{Max} \sum_{i=1}^{S} \sum_{t=1}^{T} \Lambda_{ti} - \sum_{i=1}^{S} \nu_i\left(\sum_t \Theta_{ti}+\sum_t \sum_{j \in D_i} \alpha_{ji}.r_{tj} .c_t - E_i\right)
$$

$$
= \text{Max} \sum_{i=1}^{S} \sum_{t=1}^{T} \Lambda_{ti} - \sum_{i=1}^{S} \sum_{t=1}^{T} \nu_i.\Theta_{ti} - \sum_{i=1}^{S} \sum_{t=1}^{T}\sum_{j \in D_i} \nu_i.\alpha_{ji}.r_{tj}.c_t + \sum_{i=1}^{S} \nu_i.E_i
$$

$$
= \text{Max} \sum_{i=1}^{S} \sum_{t=1}^{T} \Lambda_{ti} - \sum_{i=1}^{S} \sum_{t=1}^{T} \nu_i.\Theta_{ti} - \sum_{i=1}^{S} \sum_{t=1}^{T}\sum_{j \in A_i} \nu_j.\alpha_{ij}.r_{ti}.c_t + \sum_{i=1}^{S} \nu_i.E_i
$$

$$
= \text{Max} \sum_{i=1}^{S} \sum_{t=1}^{T} \left(\Lambda_{ti} -\nu_i.\Theta_{ti} -\sum_{j \in A_i} \nu_j.\alpha_{ij}.r_{ti}.c_t\right)+ \sum_{i=1}^{S} \nu_i.E_i.
$$

对偶问题是 $\min_{\nu_i \geq 0} D(\nu)$。 ν 是拉格朗日乘子向量，可以通过迭代进行更新

$$
\nu_i^{\ell+1} = \left[\nu_i^\ell + \gamma\left(\sum_t r_{ti}(e_t+ c_t)+\sum_t \sum_{j \in D_i} \alpha_{ji}.r_{tj} .c_t - E_i \right) \right]^+
$$

$$
= \left[\nu_i^\ell + \gamma\left(\sum_t r_{ti}.e_t+\left(\sum r_{ti}+\sum_t \sum_{j \in D_i} \alpha_{ji}.r_{tj} \right) c_t - E_i \right) \right]^+,
$$

其中 $[x]^+ = \max(x, 0)$ 且 γ是次梯度法的步长。在更新拉格朗日乘子后，求解以下优化问题以更新单个节点的采样率：

$$
\text{Max} \sum_{k=1}^{E} \theta_{tki} \log\left( \frac{w_{tki} .r_{ti}}{\theta_{tki}} \right) -\nu_i.r_{ti}(e_t+ c_t) -\sum_{j \in A_i} \nu_j .\alpha_{ij} .r_{ti} .c_t
$$

$$
\Rightarrow r_{ti} = \left[ \frac{ \sum_{k=1}^{E} \theta_{tki} }{ \nu_i(e_t+ c_t )+\sum_{j \in A_i} \nu_j .\alpha_{ij} .c_t } \right]_{R_m}^{R_M}.
$$

定理3.1. 所提出的MOP的分布式版本收敛于原始问题OP的最优解。

证明。 设$(r^ , \nu^ , \theta^ )$为MOP的最优解。可以证明$(r^ , \nu^*)$也满足原始问题OP的KKT条件。MOP的KKT条件是

由…给出

$$
\frac{\partial}{\partial r_{tki}} \left( \sum_{k=1}^{E} \sum_{i=1}^{S} \sum_{t=1}^{T} \theta_{tki} \log\left( \frac{w_{tki}.r_{ti}}{\theta_{tki}} \right) \right) \bigg| {r^ } - \sum_{i=1}^{S} \nu^ _i \left(\sum_t(e_t+ c_t)+\sum_t \sum {j \in A_i} \alpha_{ij}.c_t\right)= 0
$$

$$
\nu^ i.r {ti}^ (e_t+ c_t) - \sum_{i=1}^{S} \sum_{t=1}^{T}\sum_{j \in D_i} \nu^ i.\alpha {ji}.r_{tj}^ .c_t+ \sum_{i=1}^{S} \nu^*_i.E_i= 0
$$

$$
\nu^*_i \geq 0.
$$

请注意，OP和MOP的最后两个KKT条件是相同的。现在随着

$$
\frac{\partial}{\partial r_{tki}} \left( \sum_{k=1}^{E} \sum_{i=1}^{S} \sum_{t=1}^{T} \theta_{tki} \log\left( \frac{w_{tki}.r_{ti}}{\theta_{tki}} \right) \right) \bigg|_{r^ } = \frac{\partial}{\partial r_{tki}} \left( \sum_{k=1}^{E} \log\left( \sum_{i=1}^{S} \sum_{t=1}^{T} w_{tki}.r_{ti} \right) \right) \bigg|_{r^ },
$$

第一个 OP和MOP在点（r ∗, ν ∗）处的条件也相同。因此，证明如下 . □

我们首先需要确保执行该迭代方案所需的信息可以从邻居信息中获得。为此，我们需要修改方程(11)和方程(12)，使得节点之间仅需交换局部信息（即只需在PPs及其子节点之间进行信息交换）。我们假设节点i的总传输流量为

$$
T_i= \sum_t r_{ti} + \sum_t \sum_{j \in D_i} \alpha_{ji}.r_{tj} =\sum_t r_{ti}+\sum_{i\in P_j} \alpha_{ji}.T_j(\text{for non-leaf nodes})
$$

$$
=\sum_t r_{ti}(\text{for leaf nodes}).
$$

因此，节点可以通过收集其子节点承载的流量来计算各自的流量Ti，并利用该流量值根据公式（11）计算拉格朗日乘子。为了根据公式（12）计算各节点的采样率，我们假设$ F_i=\sum_{j \in A_i} \nu_j.\alpha_{ij} $。我们将 $ \nu_i $称作节点i的本地价格，Fi称作其聚合价格Fi。每个节点将其本地价格和聚合价格分发给其子节点，子节点再利用这些信息计算自身的聚合价格。例如，节点i通过使用其PPs的($\nu_j$, $ F_j$)来计算其聚合价格Fi：

$$
F_i=\sum_{j \in A_i} \nu_j .\alpha_{ij} =\sum_{j \in P_i} \alpha_{ij} \left( \nu_j + F_j \right)(\text{for non-CH nodes}) = 0(\text{for CH nodes}).
$$

基于此，我们现在提出一种分布式机制，用于计算节点传感器的最优采样率。在所提出的方案中，节点的流量Ti和 $ \nu_i $以自底向上的方式更新，而($F_i$, $r_{ti}$) 则以自顶向下方式更新。各节点周期性地将其 $ \alpha $广播给其邻居。若节点i存在 $|P_i|$ PPs，且其路径ETX为P‐ETXij, $ \forall j \in P_i $，当它通过节点j发送数据包时，则

$$
\alpha_{ij} = \frac{1/(P-\text{ETX} {ij})}{\sum {x \in P_i} 1/(P-\text{ETX}_{ix}) }.
$$

这是基于以下直观认识：节点根据其路由质量的比例选择路由。所有节点随后根据其本地信息计算它们的($\nu_i$, $ F_i$, $ T_i$, $ r_{ti}$) 。簇头节点向其子节点广播其聚合价格Fi为零。直接

簇头节点的子节点使用公式(16)和(12)计算其聚合价格Fi和采样率，并进行广播。在第一轮中，假设所有节点的$ \theta_{tki} $和 $ \nu_i $为某个任意值。此过程持续进行，直到到达叶节点。叶节点随后更新其承载流量Ti并进行广播。根据更新后的Ti，它们还使用方程(11)计算其 $ \nu_i $。后续的父节点使用公式(15)更新其流量及其 $ \nu_i $，该过程持续进行，直到到达簇头。在计算采样率的同时，每个叶节点i还会计算对应于每个父节点j的$ \alpha_{ij}.w_{tki}.r_{ti} $ $ \forall k $，并向其PPs广播。PPs也计算其$ w_{tki}.r_{ti} $，将其与子节点的相应值相加后（乘以$ \alpha_{ij} $）进行广播，直到传送到其簇头。

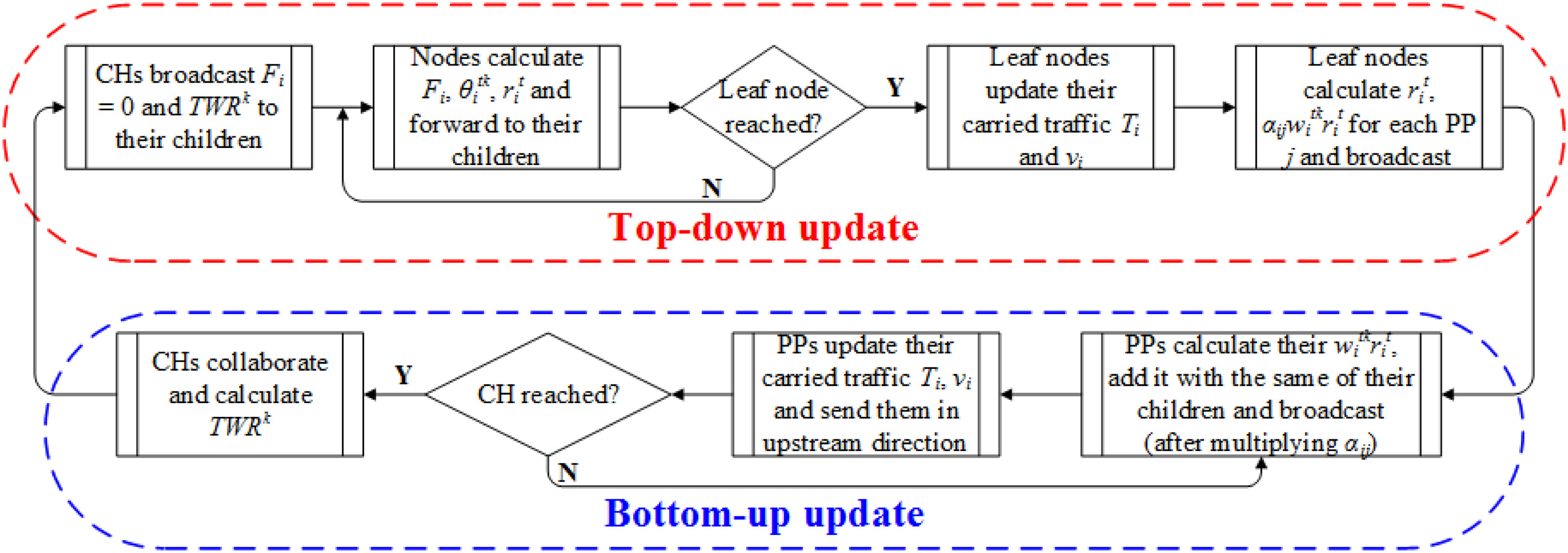
在下一次迭代中，簇头节点协作计算 $ \text{TWR} k=\sum_i\sum_t w {tki}.r_{ti} $ $ \forall k $的值，并以自顶向下方式在其各自簇内传播，节点在计算其$ \theta_{tki} $时使用该值，如公式(7)所示。这种自顶向下和自底向上的过程迭代进行。基于次梯度的分布式方案(SDS)的概念流程图如图2所示。

我们假设自顶向下和自底向上操作所需的消息交换能够成功传递到相应节点。然而在实际中，由于邻近干扰可能导致丢包。在这种情况下，可以根据相应节点发送的历史值采用一些插值机制。我们假设链路的ETX在整个迭代过程中保持不变。同时假设父子关系在整个迭代过程中保持不变，而在现实中，由于信道条件的变化，这些关系会发生变化。我们将在未来研究这些实际部署问题对该迭代方案收敛性的影响。

3.4 基于Nesterov梯度下降的分布式方案

我们提出另一种方案，使用基于Nesterov梯度下降的分布式方案(NDS)[3]通过利用对偶目标函数的Lipschitz连续性。该方案通常相较于传统次梯度方法具有更快的收敛速度；然而，在某些特定场景下，该方案的表现可能不如SDS，如第3.5节所述。

我们首先为优化问题（6）开发一个利普希茨常数。我们考虑一个 $ S\times S.T $矩阵 A，其中行表示节点集合，列表示所有传感器的集合。矩阵$ A_{ij} $中的元素表示节点i对传感器j读数的采样或传输的功耗。R和E分别是表示 $ S.T \times 1 $和 $ S \times 1 $的向量，分别代表传感器的采样率集合以及节点的可用能量。利用上述符号，问题（6）的能量预算约束可写为$ A.R \leq E $。例如，让我们考虑

图3所示的假想场景，该场景包含三个设备，每个设备配备有三个传感器。在此图中，设备1和设备2感知并将其数据包传输到设备3，因此问题（6）的能量预算约束可以写为

$$
\begin{bmatrix}
e_1+ c_1 & e_2+ c_2 & e_3+ c_3 & 0 & 0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & e_1+ c_1 & e_2+ c_2 & e_3+ c_3 & 0 & 0 & 0 \
\alpha_{13}.r_{1.1}c_1 & \alpha_{13}.r_{1.2}c_2 & \alpha_{13}.r_{1.3}c_3 & \alpha_{23}.r_{2.1}c_1 & \alpha_{23}.r_{2.2}c_2 & \alpha_{23}.r_{2.3}c_3 & e_1+ c_1 & e_2+ c_2 & e_3+ c_3
\end{bmatrix}
\begin{bmatrix}
r_{11} \
r_{12} \
r_{13} \
r_{21} \
r_{22} \
r_{23} \
r_{31} \
r_{32} \
r_{33}
\end{bmatrix}
\leq
\begin{bmatrix}
E_1 \
E_2 \
E_3
\end{bmatrix}.
$$

显然，$ A_{ij} $的任意元素的最大值为 $ \Psi= \max(e_t+ c_t) $，$ \forall t $。同时假设 $ E =\max{E_i} $ $ \forall i $，且 $ \varepsilon=\min{e_t} $ $ \forall t $，则节点对特定传感器可实现的最大采样率为 $ \Upsilon= \frac{E}{\varepsilon} $。我们还假设 $ \Omega= \max{c_t} $ $ \forall t $，$ \Gamma=\sum_t(e_t+ c_t) $，以及 $ \Delta=\sum_t c_t $。基于这些条件，我们提出以下定理。

定理3.2. 问题(6)的对偶问题是Lipschitz连续的，其常数由$ L= \frac{\rho(A^T A)}{\sigma} $给出，其中目标函数 U 是 σ-强凹函数。

证明. 请参考 Beck et al. [25]以获取证明。 □

定理3.3。 问题(6)的对偶问题是Lipschitz连续的，其常数为$ L_1= \frac{S.\Upsilon^2 (\Gamma+ (S-1) \Delta) \Upsilon+ (S-1) \Omega^2 M}{(\Gamma+ (S-1) \Delta) \Upsilon+ (S-1) \Omega} $.().(). $ \frac{E}{W_m} $，以及$ L_2= \frac{S.T .R.().().E}{W_m} $，其中$ W_m= \min{w_{tki} } $ $ \forall i, t,k $。

证明。 我们首先基于公式（5）的强凹性，推导出 σ的U：

$$
\sigma= \min\left(\frac{- \partial^2U}{\partial r_{ti}^2} \right)= \min\left(\frac{\sum_k \theta_{tki}}{r_{ti}^2} \right)= \min\left( \frac{ \sum_k w_{tki} .r_{ti}}{r_{t}^2 .\sum_{i=1}^{S}\sum_{t=1}^{T} w_{tki} .r_{ti} } \right)
= \min\left( \frac{ \sum_k w_{tki}}{r_{t} .\sum_{i=1}^{S}\sum_{t=1}^{T} w_{tki} .r_{ti} } \right) \geq \min\left( \frac{ \sum_k w_{tki}}{r_{t} .\sum_{i=1}^{S}\sum_{t=1}^{T} r_{ti} } \right) \geq \frac{E.W_m}{S.\Upsilon^2}.
$$

σ也可以用$ R_M $表示如下：

$$
\sigma \geq \min\left( \frac{ \sum_k w_{tki}}{r_{t} .\sum_{i=1}^{S}\sum_{t=1}^{T} r_{ti} } \right) \geq \frac{E.W_m}{S.T.R_M^2}.
$$

接下来，我们按如下方式计算矩阵$ A^T.A $的谱半径。在推导 $ \rho(A^T.A) $时，我们需要 $ ||A||_\infty $和 $ ||A||_1 $的值（参见方程(2)），它们分别是矩阵A的行和列的最大和。接下来，我们利用 $ \rho(A^T.A) $和 σ的值，根据定理3.2计算L：

$$
||A||_\infty \leq \sum_t(e_t+ c_t)+(S - 1)\sum_t c_t= \Gamma+(S - 1).\Delta
$$

$$
||A||_1 \leq \max_t{e_t+ c_t}+(S - 1)\max_t{c_t}=\Psi+(S - 1).\Omega
$$

$$
\therefore \rho(A^TA) \leq ||A|| 1.||A|| \infty \leq(\Gamma+(S - 1).\Delta).(\Psi+(S - 1).\Omega)
$$

$$
L_1= \frac{S.\Upsilon^2.(\Gamma+(S - 1).\Delta).(\Psi+(S - 1).\Omega)}{E.W_m} \quad \text{from Equation(19)}
$$

$$
L_2= \frac{S.T.R_M^2.(\Gamma+(S - 1).\Delta).(\Psi+(S - 1).\Omega)}{E.W_m} \quad \text{from Equation(20)}.
$$

我们假设利普希茨常数 $ L = \min{L_1,L_2} $。我们假设簇头节点计算出L并广播给其簇节点。我们利用问题(8)的对偶目标函数的利普希茨梯度性质，采用内斯特罗夫算法[3, 26]设计一种梯度下降方案。该方案如算法1所示，可由每个节点i以分布式方式实现。在算法1中，$ \Delta f $表示节点i的 $ \Delta f_i=\sum_t r_{ti}.e_t+(\sum_t r_{ti}+\sum_t\sum_{j \in D_i} \alpha_{ji}.r_{tj})c_t -E_i $。每个节点在第5行求解目标函数以获得其采样率。在第6行，$ u_i^{\ell+1} $是标准梯度下降（与方程(11)相同）在第k次迭代时步长为 $ \frac{1}{L} $的解，该解编码了当前梯度。然而，在第8行，$ v_i^{\ell+1} $是沿由所有先前迭代轮次中负梯度的加权和所确定方向进行的梯度下降步的解，因此该解编码了历史梯度。较后的迭代轮次比先前的迭代轮次具有更大的权重。最后， $ \nu_i^{\ell+1} $在第9行计算当前梯度与历史梯度的加权和。

算法1: 基于内斯特罗夫梯度下降的分布式方案(NDS)

1: 输入：Rm，RM，Wm。
2: 输出：采样率 $ r_{ti} $ $ \forall i \in{1, 2,…，N} $。
3: tmpi= 0；
4: 对于每次迭代 $ \ell={1, 2,…， L} $执行
5: 更新速率 $ r_{ti} $ 和 $ \theta_{tki} $ ；
6: $ u_i^{\ell+1} =[\nu_i^\ell+ \frac{\Delta f_i}{L}] + $；
7: tmpi= tmpi+ $ \frac{\ell+1}{2}.\Delta f_i $；
8: $ v_i^{\ell+1} =[\frac{\text{tmpi}}{L}] + $；
9: $ \nu_i^{\ell+1} = \frac{\ell+1}{\ell+3}.u_i^{\ell+1} + \frac{2}{\ell+3}.v_i^{\ell+1} $；
10: 结束循环

3.5 SDS和NDS的验证

我们假设了一个用于监测变电站电力设备健康状况的假想场景。传感器节点使用电池供电，假设电池容量为5000毫安时[17]。除非另有说明，我们假设节点采用异步低功耗监听（ X‐Mac），使其大部分时间处于睡眠状态，并定期唤醒以检查信道活动。该

=(1, 30)条件下收敛性(a)、SDS采样率(b)和NDS采样率(c)的比较。在(Rm, RM) =(1, 300)条件下收敛性(d)、SDS采样率(e)和NDS采样率(f)的类似比较。)

节点每秒唤醒八次以检查信道是否繁忙，这使得用于传输的无线电开启时间约为140毫秒。节点在发送模式下的功耗约为20毫安[27]，该参数代表了Crossbow公司的MICAz无线传感器节点，这些节点配备了运行在8兆赫的Atmel ATmega128L处理器、2.4吉赫 Chipcon CC2420无线电、128千字节程序存储器、512千字节测量闪存和4千字节 EEPROM[27]。预计节点将保持活跃状态12个月，感知和转发的功率预算据此计算得出。节点使用其传感器：声音、SF6气体和温度。这些传感器的功耗分别为9.5、150和7.5毫安，采样时间分别为7,000、400和112毫秒[17]。

我们将所提出的MOP的分布式速率自适应方案与通过AMPL求解器获得的OP的解进行比较[28]。结果如图4所示，其中14个节点在高度为3的二叉树结构中部署，根节点为簇头CH，且所有节点的电池均为满电状态。Rm和 $ w_{tki} $分别假设为每小时1次和0.5。我们假设SDS的步长 γ为 $ \frac{1}{L} $。我们根据 $ R_M $的值考虑两种情况；在第一种情况（图4(a)–(c)）中，$ R_M $假设为每小时30次，而在第二种情况（图4(d)– (f)）中则假设为每小时300次。注意，在第一种情况下，NDS在收敛速率方面表现明显不如SDS。我们推测，由于 $ R_M $较小，根据公式(12)计算出的 $ r_{ti} $经常等于$ R_M $，因此跟踪历史梯度并不能使该方案更快。然而，在第二种情况下，NDS在收敛速度方面优于SDS，如图4(d) 至 (f) 所示。在这两种情况下，我们观察到MOP的分布式版本与原问题(4)(a) 为了清晰起见未显示最优解)非常接近，这验证了定理1的结论。6) 图4（b）和（c）以及图4（e）和（f）显示了节点1、3和7的采样率，这些节点分别是二叉树中一级、二级和三级节点的代表。从这些图中可以看出，在电池电量相同的情况下，一级节点的采样率高于其他节点。这是因为将更多的采样任务分配给一级节点可以减少转发流量的影响，从而提高整体效用。我们还可以观察到，在SDS和NDS方案中，由于迭代次数较多（数百到数千次量级），收敛时间显著增加，这限制了它们在大规模无线传感器网络应用中的实用性。

3.6 跳数的影响

从节点到簇头的跳数与收敛时间之间存在明显的权衡关系。当节点到簇头的跳数增加时，收敛时间也随之增加。图5展示了不同跳数对收敛时间的影响。我们在保持节点数量不变的情况下，根据最大树高调整了二叉树拓扑结构。从图5中可以看出，当树高从3降低到1时，收敛时间减少。图5（c）显示了节点3的采样率，也验证了较小的树高能够实现更快的收敛速度。然而，为了降低最大树高或减少跳数，需要在目标区域部署更多的簇头节点，这会增加部署与维护成本。因此，这种权衡体现在部署成本与收敛速度之间。

SDS在(Rm, RM) =(1, 300)下的收敛情况。(b) NDS在(Rm, RM) =(1, 30)下的收敛情况。(c) 节点3的采样率。)

4 可扩展的半分布式替代方案

由于完全分布式版本的收敛时间对于一般的多跳网络来说过高，在节点层级上解决此问题仅出于以下原因而不切实际：

• 为了实现这些完全分布式方案，节点与簇头之间需要交换过多的控制消息，这将耗尽它们的电池电量。
• 然而，由于地理区域内的节点数量众多，这些方案的收敛时间显著增加。

高收敛时间的主要原因是多跳传输，因为单个节点及其祖先节点需要逐步调整其采样率，以确保在转发来自后代节点的流量时，高层级节点（祖先节点）不会耗尽电池电量，同时最大化整体效用。因此，前述的分布式方案不具备可扩展性，尤其不适用于大规模无线传感器网络。接下来，我们提出两种替代方案来克服这一限制。第一种方案是一种半分布式方法，其中簇头节点协作并决定各节点的采样率，前提是收集了所有节点的拓扑信息和电池状态。第二种替代方案基于节点间数据包传输的假设

遵循一些预定的机制，因此数据转发导致的功耗可以忽略不计。

4.1 一种半分布式协作方法

我们提出了一种半分布式速率自适应（SDRA）方案，其中簇头节点收集其所在簇内节点的拓扑信息和剩余电池电量，然后相互协作以迭代方式决定各节点的采样率。整体方案如算法2所示。我们假设有 C个簇头节点，其中簇头β关联一个包含 $ \zeta_\beta $个 $ S_\beta $节点的集合。因此，簇头节点以分布式方式求解C个子问题，这些子问题通过参数$ \theta_{tki} $ 相关联。首先，簇头节点收集所需连接信息和节点的剩余电池容量。每个簇头 β 使用8）在本地求解问题（使用 $ S= S_\beta $ 和$ i \in \zeta_\beta $ ），这可以通过任何现有的求解器完成，例如 AMPL、GLPK 和 CVX。随机 $ \theta_{tki} $ （在第一次迭代时），可以使用任何现有求解器完成，例如 AMPL、GLPK 和 CVX。然后计算其本地加权速率$ \text{WR} {k\beta} =\sum {i\in\zeta_\beta} \sum_t w_{tki} .r_{ti} $ $ \forall k $并将其广播给其他簇头节点。簇头节点协同计算总加权速率$ \text{TW R} k =\sum \beta \text{WR} {k\beta} =\sum_i\sum_t w {tki} .r_{ti} $ $ \theta_{tki}= \frac{w_{tki} .r_{ti}}{\text{TWR} k} $。然后簇头节点计算$ \frac{w {tki} .r_{ti}}{\text{TWR} k} $（公式（7））并使用新的 $ \theta {tki} $求解其本地优化问题。此过程持续进行直到解收敛。收敛后，簇头节点将计算出的采样率发送给相应节点。整体方案如图6所示。

请注意，在簇的数量、它们之间的消息交换次数以及弹性之间存在一种内在的权衡。较少的簇数量会减少它们之间的消息交换次数，但在节点/链路故障（相对于某个固定的误差容限）或攻击方面弹性较差；而更多的簇则以较高的控制开销为代价提高了弹性。

4.2 调度型无线传感器网络的一种近似方案

我们还提出了一种用于分布式速率自适应（ADRA）的近似方案，该方案仅适用于调度型无线传感器网络。在调度型无线传感器网络中，节点按照各自的调度时间唤醒。节点知晓其邻居的调度信息，因此它们等待其父节点的调度，在特定时间开启发射器并进行传输。在这种情况下，节点无需像X‐Mac中那样发送多个脉冲数据包，从而使得传输功耗非常低。此时，能量预算方程（$ \sum_t\sum_{j \in D_i} \alpha_{ji}.r_{tj}.c_t $在公式（8）中的第二项）可以忽略不计。因此，问题（8）中的多跳项被忽略，问题简化为如下形式：

ADRA Problem:

$$
\text{Maximize} \sum_{k=1}^{E} \log\left( \sum_{i=1}^{S} \sum_{t=1}^{T} w_{tki} .r_{ti} \right)
$$

$$
\text{subject to} \sum_{t} r_{ti}(e_t + c_t) \leq E_i \quad \forall i
$$

$$
R_m \leq r_{ti} \leq R_M \quad \forall i,\forall j,\forall t.
$$

通过使用类似于公式(7)的詹森不等式，我们得到

改进的ADRA问题(MADRA)：

$$
\text{Maximize } U= \sum_{k=1}^{E} \sum_{i=1}^{S} \sum_{t=1}^{T} \theta_{tki} \log\left( \frac{w_{tki}.r_{ti}}{\theta_{tki}} \right)
$$

$$
\text{subject to} \sum_{t} r_{ti}(e_t+ c_t) \leq E_i \quad \forall i
$$

$$
R_m \leq r_{ti} \leq R_M \quad \forall i,\forall j,\forall t.
$$

根据公式（7），我们可以证明，求解公式（22）中的MADRA等价于求解公式（23）中的ADRA。对于给定的$ \theta_{tki} $ ，MADRA是严格凹函数，因此可以使用算法3求解。在此方案中，节点首先为每个传感器i分配采样率$ r_{ti}= \frac{E_i. \sum_k \theta_{tki}}{\sum_i\sum_k \theta_{tki} (e_i+c_i)} $（第3行）。如果某个传感器的采样率低于或高于指定阈值Rm和RM，则该节点将 Δ公平地分配给其他传感器（第5–24行）。节点首先初始化一个空集合V（第4行）。如果某传感器的采样率小于Rm，则将其采样率调整为Rm，并将该传感器加入集合V，然后将 Δ公平地分配给不在集合V中的传感器。此过程对所有传感器重复执行（第5–14行）。之后，当任意传感器的采样率高于RM时，同样应用该过程（第15–24行）。

Theorem 4.1. 对于给定的$ \theta_{tki} $ ，算法3给出了节点传感器的最优解速率分配。

证明。 第3行可以通过求解问题方程（8）的拉格朗日函数和KKT条件（忽略最后一组约束）得到，如下所示：

$$
L= \sum_{k=1}^{E} \sum_{i=1}^{S} \sum_{t=1}^{T} \theta_{tki} \log\left(\frac{p_{tki}.r_{ti}}{\theta_{tki}} \right) - \sum_{i=1}^{S} \lambda_i\left(\sum_t r_{ti}(e_t+ c_t) - E_i\right),
$$

$$
\frac{\partial L}{\partial r_{ti}} = \frac{\sum_{k=1}^{E} \theta_{tki}}{r_{ti}} - \lambda_i(e_t+ c_t)= 0,
$$

$$
\lambda_i\left(\sum_t r_{ti}(e_t+ c_t) - E_i\right)= 0.
$$

公式(25) 给出 $ r_{ti} = \frac{\sum_{k=1}^{E} \theta_{tki}}{\lambda_i (e_t +c_t)} $ 和 $ \lambda_i \geq 0 $。将其代入公式(26)，得到 $ \lambda_i= \frac{\sum_{t=1}^{T}\sum_{k=1}^{E} \theta_{tki}}{E_i} $，从而得出 $ r_{ti} = \frac{E_i . \sum_k \theta_{tki}}{\sum_{t=1}^{T}\sum_{k=1}^{E} \theta_{tki} (e_t +c_t)} $。

在计算出采样率后，节点计算$ \alpha_{ij} .w_{tki} .r_{ti} $ $ \forall k $并将其广播给它们的PPs，用于如SDS中所述在簇头节点处计算$ \text{TWR} k =\sum_i\sum_t w {tki} .r_{ti} $ $ \forall k $。利用新的$ \text{TWR} k $，节点接下来通过将新的$ \theta {tki} $ 输入ADRA来计算传感器的更新后的采样率，并且此过程持续进行直到解收敛。

4.3 SDRA和ADRA的验证

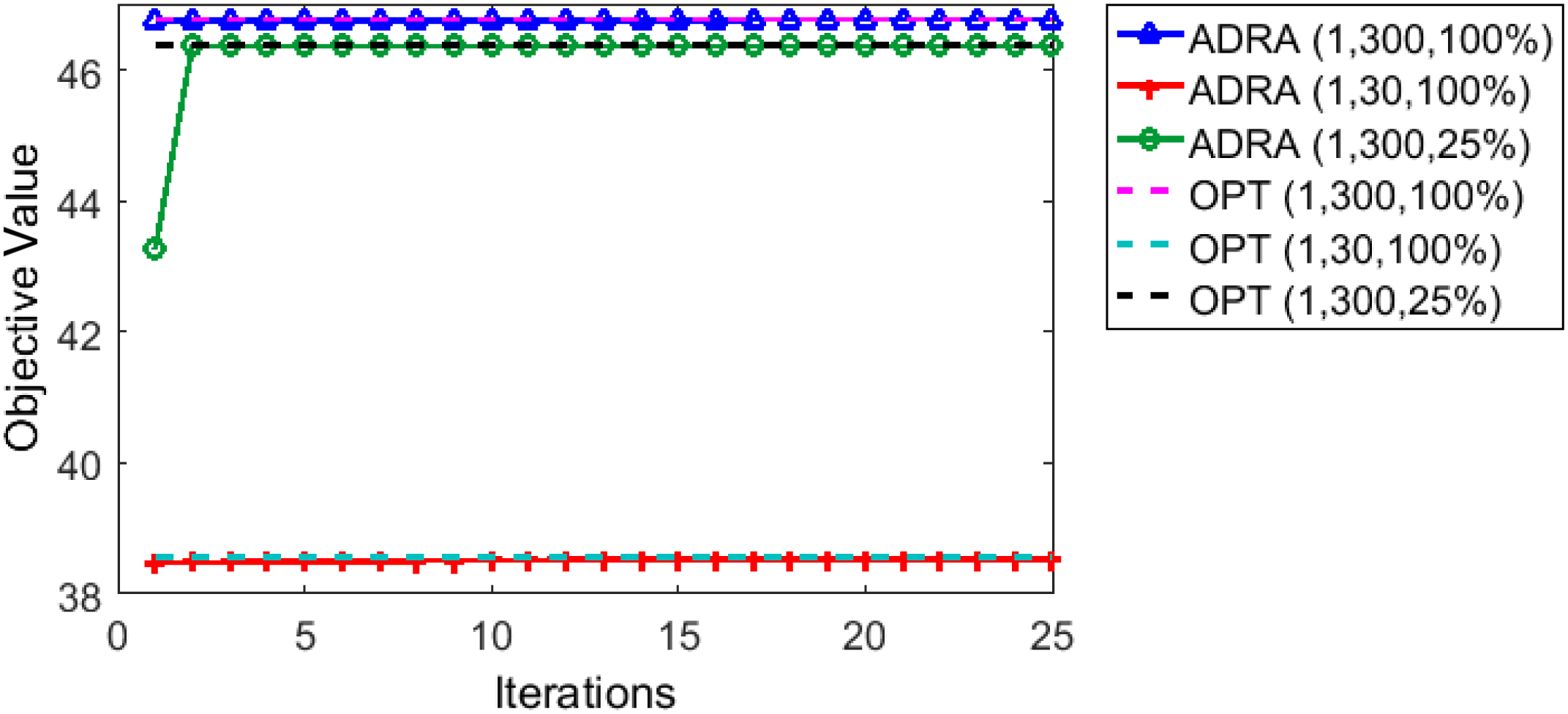
为了验证SDRA和ADRA的收敛性，我们假设一个包含五个簇的场景，每个簇包含14个节点，以高度为3的二叉树结构排列。图7和图8展示了这两种方案在不同剩余电池容量和 $ R_M $下的目标值收敛情况。从这些图中可以看出，两种方案的目标值均与从AMPL获得的最优解相匹配。我们还可以观察到，这两种方案收敛速度相当快（大约在10

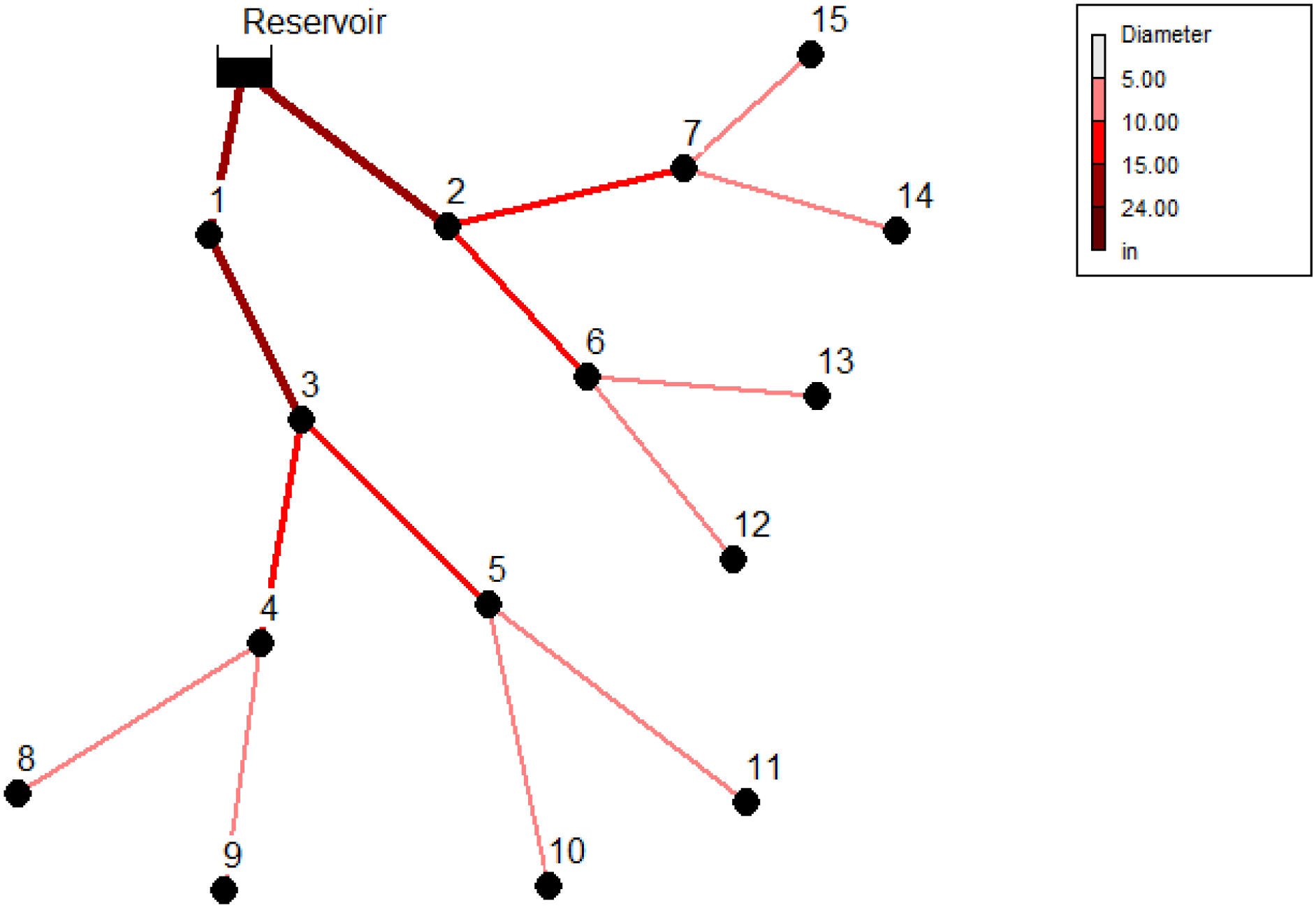
15次迭代），这使得它们成为能量受限的无线传感器网络中的可扩展解决方案。同时请注意，目标值随着剩余电池容量和RM的增加而增加，这是由于单个传感器的采样率提高所致。图7(b) 显示了树高对 SDRA 收敛的影响，当RM假设为 300 且电池容量假设为 100% 时。该图表明了

算法3： 分布式速率自适应近似方案（ADRA）

1: 输入 : $ \theta_{tki} $, Rm, RM.
2: 输出 : 采样率 $ r_{ti} $ $ \forall i $.
3: $ r_{ti}= \frac{E_i. \sum_k \theta_{tki}}{\sum_t\sum_k \theta_{tki} (e_i+ c_i)} $ $ \forall t $;
4: V = {ϕ};
5: 对每个传感器 t ={1, 2,. . . , T}执行
6: 如果 $ r_{ti}< R_m $则
7: 分配 $ r_{ti} = R_m $;
8: V = V ∪t;
9: Δ= $ E_i -\sum_i r_{ti}(e_i+ c_i) $;
10: 对 V 中的每个传感器 m ’ 执行
11: $ r_{mi} = r_{mi} + \frac{\sum_k \theta_{mkj}}{\sum_{m’}\sum_k \theta_{mki}} . \frac{\Delta}{(e_m+c_m)} $;
12: 结束循环
13: 结束如果
14: 结束循环
15: 对每个传感器 t ={1, 2,. . . , T}执行
16: 如果 $ r_{ti} > R_M $则
17: 分配 $ r_{ti} = R_M $;
18: V = V ∪t;
19: Δ= $ E_i -\sum_i r_{ti}( e_t + c_t) $;
20: 对 V 中的每个传感器 m ’ 执行
21: $ r_{mi} = r_{mi} + \frac{\sum_k \theta_{mkj}}{\sum_{m’}\sum_k \theta_{mki}} . \frac{\Delta}{(e_m+c_m)} $;
22: 结束循环
23: 结束如果
24: 结束循环
25: 返回 $ r_{ti} $ $ \forall t $

应用	传感器类型	电流/功耗
变电站监控	振动/声音	9.5 毫安
变电站监控	SF6气体传感器	150 毫安
变电站监控	环境温度	7.5 毫安
灾害监测	摄像机	1,258 毫瓦
灾害监测	麦克风	329 毫瓦
灾害监测	加速度计	96 毫瓦
管道监控	氯传感器	4 mA
管道监控	ORP	20.2 毫安
管道监控	pH	25.5 毫安

在 SRDA 情况下，多跳对收敛时间的影响大大降低，这满足了使用该方案的主要要求。我们还可以观察到，由于从节点到簇头节点的跳数较少，目标值随着树高的减小而增加。在 ADRA 情况下，多跳的影响被忽略，因此该方案不依赖于树高。

5 协同感知性能评估

我们在三种不同的应用场景中评估了自适应方案。首先，我们在变电站监控场景中评估这些方案，其中传感器节点部署在不同的电气设备上。接着，我们在灾害监测场景中评估该方案，多个智能手机被部署用于监测特定的兴趣点以进行态势监控。最后，我们在管道监控场景中评估自适应效果，其中监测设备配备了多个异构传感器，用于感知不同的水污染物。对于所有这些实验，我们假设采用调度传输，因此忽略了前导码长度。构建此类设置的目的是为了展示在配备多传感器的设备存在的情况下协同感知的效果。这些场景中使用到的不同传感器及其电流/功耗如表2所示。

5.1 自适应在变电站监控中的影响

5.1.1 实验设置。

我们首先研究所提出的采样率自适应方案在变电站监控场景中的有效性，其中每个设备都配备了一个振动

传感器、一个SF6密度传感器和一个温度传感器。这些传感器的功耗分别为9.5、150和7.5毫安，采样时间分别为7000、400和112毫秒，由此产生的功耗如表2所示。假设MicaZ传感器节点在发送模式下的功耗约为20毫安[27]。这些节点使用CC2420无线电模块，属于分组级无线电，最大包长度为127字节，数据速率为250 kbps[34], resulting in a transmission time of approximately 4 ms. The devices are uniformly deployed in a geographic area of 200 × 200平方米。节点的满电电池容量假设为5000毫安时[35,36]。节点的剩余电池容量在(25 %至100%)范围内均匀随机选择。根据其剩余电池容量，这些设备被划分为三个层级。第一、第二和第三层级节点的电池电量分别为(75%至100%)、(50%至75%)和(25%至50%)。Rm和R M分别假设为每小时1次和每小时30次。节点预计将持续活跃12个月。

5.1.2 实验结果。

图9(a) 显示了不同层级节点的平均能量预算，而图9(b) 显示了相应的使用情况，其定义为累积的设备因采样和转发数据包而导致的能量消耗。从图9(b)中可以看出，能耗根据单个节点的功率预算成比例地调整。图9(c)至(e)显示了声音传感器、SF6气体传感器以及不同层级的温度传感器的平均采样率。我们可以观察到，由于第一层节点具有更高的电池电量，其采样率明显高于其他层级。我们还可以观察到，声音传感器捕获的平均采样数量远少于另外两种传感器（大约为14到25倍）。原因在于声音传感器在数据采集时具有较高的功耗。图9(f)展示了各种传感器的总体采样率，这也证实了所提出的方案通过主要关闭高功耗传感器来节约能量。这表明所提出的方案能够适应单个节点的功率预算以及单个传感器的功耗。

我们还可以观察到，即使整个网络的总流量随着节点数量的增加而增加，单个传感器的采样率也不会随节点数量发生显著变化。这是由于节点的均匀分布，使得即使累积网络流量随节点数量增加而增长，单个节点的平均数据转发次数也大致相同。

5.2 自适应在灾害监测中的影响

5.2.1 实验设置。

我们现在研究在灾害监测场景中采样率自适应方案的使用，其中少数智能手机利用附带的传感器共同监控情况。模拟系统拓扑包括75个设备和五个接入点，分布在 100 × 1000平方米的区域内。每个接入点关联一个由14部智能手机组成的集群，这些智能手机以高度为3的二叉树结构排列。假设充满电的手机电池容量为11.78瓦时，这通常是当前智能手机的典型容量。手机需要持续工作24小时，据此计算感知和转发的功率预算。手机使用三种传感器：摄像机、麦克风和加速度计。这些传感器的功耗分别为1,258、 329和96 毫瓦[33],，采样时间为5秒（近似来自Wang等人的研究[37]）。数据包的数据有效载荷大小假设为1千字节。假设无线传输速率为10兆比特每秒。假设这些手机使用其 Wi‐Fi无线电模块进行数据包传输，在发送状态下的功耗约为1000毫瓦[38]。

5.2.2 实验结果。

接下来，我们讨论手机采样率自适应的性能，该性能取决于其剩余电池容量。手机的剩余电池容量在(25%至100%)范围内均匀随机选择。根据电池容量，我们将手机分为三个层级。第一层、第二层和第三层手机的电池电量分别为(75%至100%)、 (50%至75%)和(25%至50%)。 Rm和RM分别假设为每小时12次和每小时120次。图10(a) 显示了不同层级手机的平均能量预算，图10(b) 显示了相应的使用情况。使用情况定义为由于数据采样和数据包转发所产生的累积能耗。从图10(b) 中可以看出，手机的使用情况与其功率预算成正比。图10(c) 至(e) 显示了