汉诺塔问题（分治递归）笔记与分析

原创已于 2025-07-24 02:00:48 修改 · 295 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#笔记 #算法

于 2025-07-24 01:56:37 首次发布

下附问题：

题目描述：
传说在古印度的一个寺庙里，有三根柱子，第一根柱子上从下到上按大小顺序叠放了64个金盘。僧侣们需要将这些金盘全部移动到第三根柱子上，移动过程中必须满足以下规则：1.每次只能移动一个盘子；2.盘子只能从顶部移动到另一根柱子的顶部；3.任何时候，在三根柱子的任何一根上，较大的盘子不能放在较小的盘子上面。编写一个函数，输出将所有盘子从第一根柱子移动到第三根柱子的移动步骤。

解决代码：

/*
 *该代码使用分治与抽象思想，
 *在函数实现时假定本函数拥有需实现的功能
 *将n层汉诺塔的移动拆分成先移动n-1层多层汉诺塔，再移动第n层到目的杆，再移动前n-1层到目的杆的问题
 *再将每一个“移动前n-1层”作为单独的子“移动n层”问题求解
 *从而分治求解
 */

#include <iostream>

using namespace std;
void hanoi (int n, char from, char to, char aux);   // 定义汉诺塔函数，该函数的作用是将n层汉诺塔从from、移动到to
int main()
{
    // variable definition

    int n;          // 汉诺塔的层数


    // variable assignment

    cout << "Enter the number of disks: ";
    cin >> n;


    // operation

    hanoi(n, 'A', 'C', 'B');    // 将n层汉诺塔从A移动到C


    return 0;
}

// 函数实现

void hanoi (int n, char from, char to, char aux)
{
    // 特殊情况：需移动汉诺塔只有一层时

    if (n == 1)                                                                 // 当只剩一层汉诺塔时
    {
        cout << "Move disk 1 from " << from << " to " << to << endl;    // 进行移动
        return;                                                                 // 移动后终止操作
    }


    // 通常情况，在移动非零n层汉诺塔时，可分为三步

    /* 移动前n-1层汉诺塔到暂存柱子 */
    hanoi(n - 1, from, aux, to);

    /* 将第n层移动到目标柱子 */
    cout << "Move disk " << n << " from " << from << " to " << to << endl;

    /* 将前n-1层移动到目标柱子 */
    hanoi(n - 1, aux, to, from);


}

一、思路分析

解决方案使用分治法的思路，先将原问题化解成简单的问题：移动n层汉诺塔时，需要先将n-1层汉诺塔移动到暂存柱子中（步骤1），然后将最后一层移动到目标柱子位置（步骤2），然后将前n-1层汉诺塔移动到目标柱子上（步骤3）。

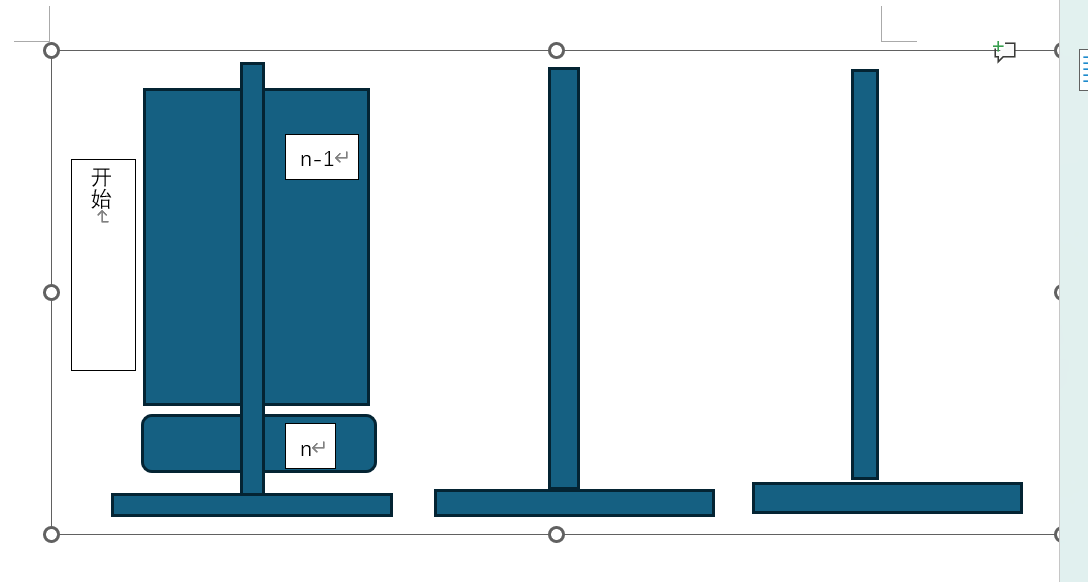
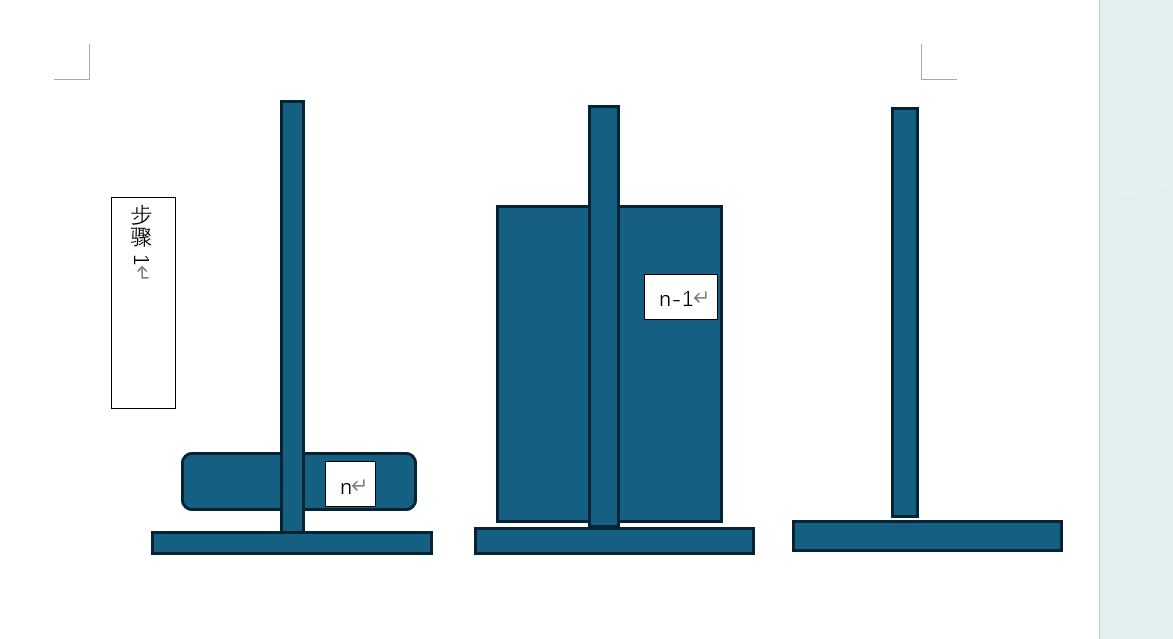
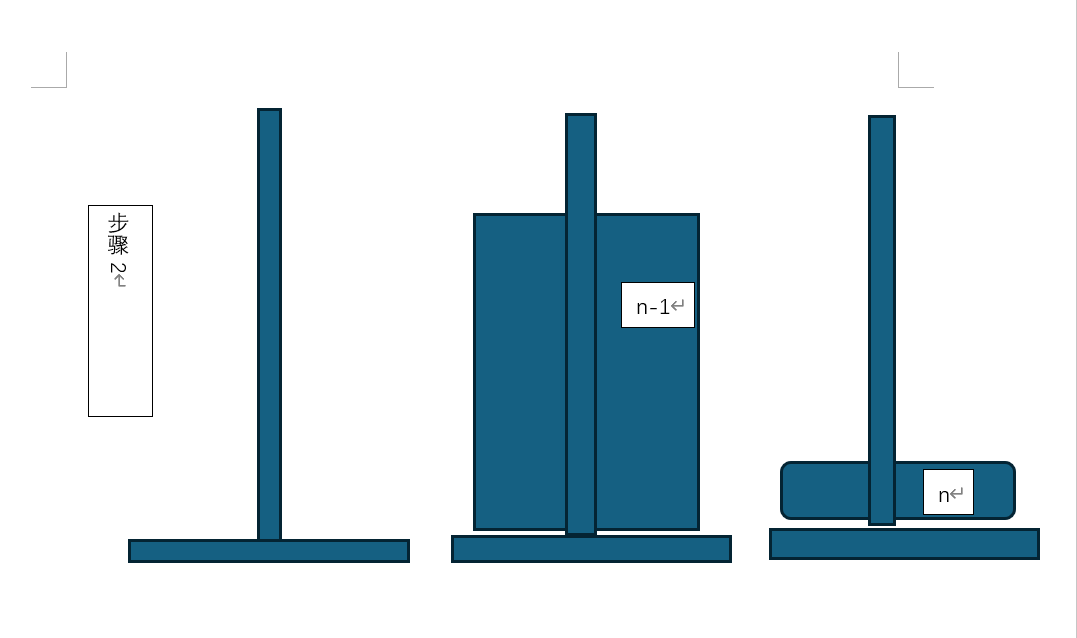
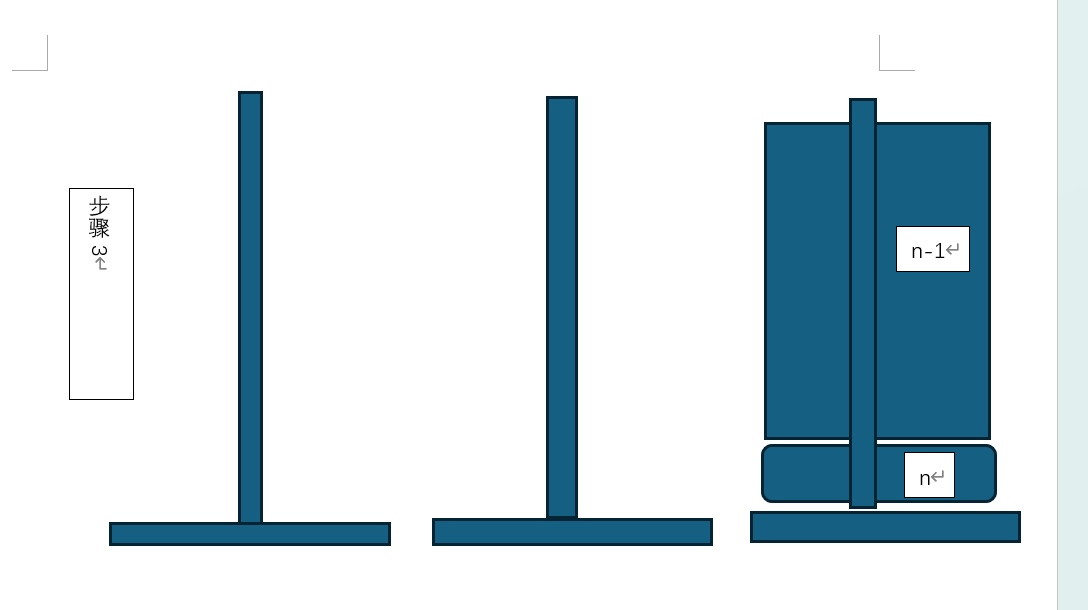
步骤2是一个的简单操作，而步骤1和3则是与原问题（移动n层汉诺塔）相似的子问题（移动n-1层汉诺塔）。（在n=1时，由于解决问题无需移动前n-1层，所以此时使用特例终止调用。）

由于子问题与原问题相似，所以移动操作几乎一致，所以此时我们在实现时可以抽象的假定hanoi已经实现，所以在完成实现时，调用hanoi函数本身完成对n-1层汉诺塔的移动，从而简化hanoi函数的代码实现

二、原理解释

首先，如果hanoi可以移动n-1层汉诺塔，则实现时，先将前n-1层移动到暂存，再将n层移动到目标杆子，然后从暂存一次性将前n-1层移动到目标杆子三个操作分别一定可以实现，那么hanoi就一定可以移动前n层汉诺塔。

在移动n层汉诺塔时，如果Hanoi函数可以移动n-1层汉诺塔，那么它就一定可以完成对n层汉诺塔的移动，同理，如果hanoi可以移动n-2层汉诺塔，那么hanoi一定可以移动前n-1层汉诺塔，......，如果可以移动2层汉诺塔就可以移动三层汉诺塔，而只要能移动1层汉诺塔，就一定可以移动2层汉诺塔，由于一层汉诺塔属于单层，通过特例情况代码一定可以移动，可以递推得到：由于1层可以移动，则2层汉诺塔可以移动，由于二层汉诺塔可以移动，则三层汉诺塔可以移动，由于三层汉诺塔可以移动，则.....，由于n-1层汉诺塔可以移动，则n层汉诺塔可以移动，即由此推得实际实现的hanoi函数可以实现n层汉诺塔的移动，所以在hanoi函数实现内部调用的Hanoi函数也能实现对n-1层汉诺塔的移动

由此闭环