初学狄克斯特拉算法~（待提高）

读书笔记

• 狄克斯特拉算用来寻找加权图的“最短路径”（不一定是段数最少，我们需要一定的量度，比如说最少花费，最短时间等，bfs只是解决了段数的最短路径问题）
• 鉴于无向图就是一个环，而此算法只适用于有向无环图！
• 权重永不能为负！否则狄克斯特拉算法失效（使用贝尔曼-福德算法？？）
• 大致步骤：

1. 找出起点出发权重最小的节点A（遍历起点的邻居），记录起点邻居的“开销”（从起点一步步来到该点的当前可知的最短步数，适用于所有的节点），其余的节点开销为无穷大，此外还需记录每一个节点的父节点（可以导致当前开销的上一个节点，随开销的更新而更新）
2. 遍历A的邻居，检查从A出发到此是否可以缩短其开销，如果缩短了就更新此节点的开销（无穷大的意义在此），同时更新父节点，这个操作遍历A的所有未被检查过的邻居
3. 检查完毕我们可以将A标记为已经经检查过了（专门的记录数组），然后返回过程1，直到所有的节点都被标记检查过了
4. 结合记录下的父节点从终点到起点“顺藤摸瓜”，其路径就是最短权重路径！
   （进一步学习通道：Dijkstra（简单的狄克斯特拉算法Python实现））

代码尝试

（能力有限，其实是抄袭的当作练习了~注释是自己的。。。）
（感谢膜拜大佬！）
殊不知自己摸到了最小生成树，尽可能理解一下吧：

#include<iostream>
#include<cstdio>
using namespace std;
#define INF 100000000//足够表示无穷大了 
#define MAXNODE 100//最高的节点数目，视情况而定，我给的例子数目很小的 
typedef int infotype;
typedef struct {
	int node;//顶点的编号（从 0 开始） 
	infotype info;//顶点的其他信息 
}VertexType;//结构名 
typedef struct {//定义图 
	int edges[MAXNODE][MAXNODE];//临接矩阵 
	int n, e;//定点数，弧数 
	VertexType vexs[MAXNODE];//存放顶点信息 
}MGraph;
void Ppath(int path[], int i, int v) {//依照 path[] 存放的“父节点”顺藤摸瓜查找路径上的节点，递归思想！！ 
	int k;
	k = path[i];// k 是 i 的“父节点” 
	if (k == v) return;//找到了起点则返回
	Ppath(path, k, v);//找顶点 k 的前一个节点 
	cout << k << ',';//输出顶点 k 
}
void Dispath(int dist[], int path[], int s[], int n, int v) {//输出最短路径 
	int i;
	for (i = 0;i < n;i++) {
		if (s[i] == 1) {//被检查完毕的节点已经得出了最短路径 
			cout << "从" << v << "到" << i << "的最短路径长度为：" << dist[i] << "\t路径为：";
			cout << v << ',';//路径起点 
			Ppath(path, i, v);//路径上的中间点 
			cout << i << endl; //路径的终点 
		}
		else cout << "从" << v << "到" << i << "不存在路径" << endl;
	}
}
void Dijkstra(MGraph g, int v) {
	int dist[MAXNODE], path[MAXNODE];
	int s[MAXNODE];
	int mindis, i, j, u;
	for (i = 0;i < g.n;i++) {
		dist[i] = g.edges[v][i];//距离初始化 
		s[i] = 0;//s[] 置空，表示暂时未被标记，该函数到这里只是检查源点的所有邻居 
		if (g.edges[v][i] < INF) path[i] = v;//“父节点”更新 
		else path[i] = -1;//暂未找到“父节点” 
	}
	s[v] = 1;//标记初始点检查完毕（所有邻居遍历完毕） 
	path[v] = 0;
	for (i = 0;i < g.n;i++) {//循环直到所有顶点的最短路径都求出 
		mindis = INF;//mindis 放置最小长度初值 
		for (j = 0;j < g.n;j++) {//选取不在 s 中并且具有最小距离的顶点 u 
			if (s[j] == 0 && dist[j] < mindis) {
				u = j;mindis = dist[j];
			}
		}
		s[u] = 1;//顶点 u 加入 s 
		for (j = 0;j < g.n;j++) {//修改不在 s 中的顶点的距离 
			if (s[j] == 0) {
				if (g.edges[u][j] < INF && dist[u] + g.edges[u][j] < dist[j]) {
					dist[j] = dist[u] + g.edges[u][j];path[j] = u;//更新 u 的邻居的最短路径及“父节点” 
				}
			}
		}
	}
	Dispath(dist, path, s, g.n, v);//输出最短路径 
}
int main() {
	int i, j;
	MGraph g;
	g.n = 7;g.e = 12;
	int a[7][MAXNODE] = {
		{0,4,6,6,INF,INF,INF},
		{INF,0,1,INF,7,INF,INF},
		{INF,INF,0,INF,6,4,INF},
		{INF,INF,2,0,INF,5,INF},
		{INF,INF,INF,INF,0,INF,6},
		{INF,INF,INF,INF,1,0,8},
		{INF,INF,INF,INF,INF,INF,0}
	};
	for (i = 0;i < g.n;i++) {
		for (j = 0;j < g.n;j++) {
			g.edges[i][j] = a[i][j];
		}
	}
	cout << "最小生成树构成：" << endl;
	Dijkstra(g, 0);
	cout << endl;
	return 0;
}
/*终极注释：
看一看我们狄克斯特拉算法需要的因素对应的成分：
edges[][]：生成邻接矩阵，就是我放的表格，存放输入数据
node：顶点的编号，记录每一个节点
MGraph.n: node 的个数
MGraph.e：边的个数
dist[]：最短路将，比如 dist[1] 代表从 v（源点）到 1 的最短路径（加权）
path[]：记录当前发现的最短路径的节点的“父节点”，不断更新
s[]：记录节点是否被检查过了，检查完毕就标记
void Dijkstra(MGraph g,int v) 函数实现过程体现了狄克斯特拉算法的流程，
需要我细细咀嚼，我竟然理解了！！下面要靠自己勤于练习会自己写代码啦！*/

额，这个输入的图有点抽象，我解释一下：

进一步解释

首先根据邻接矩阵画出来是这样：

我们规定左上角坐标（0，0），右下角（6，6），以此类推，对于每一个位置，规定对应的数值为f(x,y),那么我们这样说：
从 x 到 y 的路线权重为 f(x,y)（注意叉号指的是无穷大）
我们要找到所要求的最小权重路线，本文中使用狄克斯特拉算法实现，下面是我们根据上表画出来的关系图：

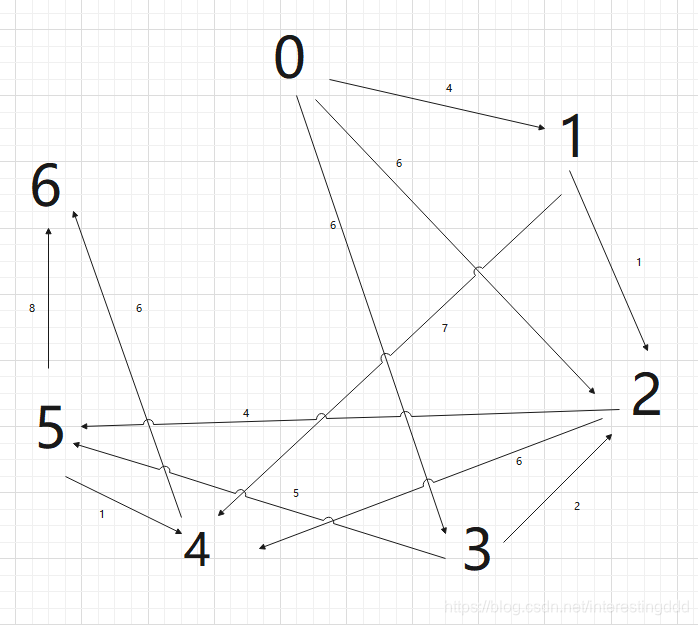
符合狄克斯特拉算法的使用条件，所以接下来好好理解上面的代码吧！（重要信息放在注释了~）
附：贝尔曼·福德算法思想