本文借鉴了这篇文章https://blog.youkuaiyun.com/DaDaMr_X/article/details/51265230
离散数学又被称为计算机数学,本篇文章就介绍了如何用C++实现求离散数学中的主范式
要求主范式,具体可分为以下几步操作:
首先,由于某些特殊符号不好在计算机中打出,因此需要用相应的符号代替,并定义各个运算符的优先级,如下
| 现符号 | 优先级 | |
|---|---|---|
| 非 | ! | 5 |
| 合取 | & | 4 |
| 析取 | | | 3 |
| 条件 | - | 2 |
| 双条件 | + | 1 |
接下来需要按运算符优先级对公式进行转换,然后用位运算的方式写出五种运算符的运算方法
假设有两个命题变元a,b(计算时a,b的值为0或1),下面列出位运算方法(可以举例子试一下):
非运算:非a: return (a+1)&1;(例如,a为1,a+1=2, 2在二进制中的表示为10,而位运算是取二进制形式的最后一位数进行运算,则为0&1,
其结果显然为0,即返回值为0,达到了非a的运算效果,以下运算方式类似)
合取:a&b: return a*b;
析取:if(a+b) return 1;else return 0;
条件:if(a==1 && b==0) return 0;else return 1;
双条件:return !((a+b)&1);
然后需要写一个函数来对所有存在的命题变元进行赋值,每个命题变元都有0和1两种情况,这一步可以采用递归来写(具体见代码),每完成一组赋值后都要都要以该组赋值情况确定下标(例如,有a,b,c,三个命题变元,假设某组赋值为101,则其下标为1*(2^0)+1*(2^2)=5,则最后输出范式时下标就为m5或M5,至于是主析取范式还是主合取范式则需看该组赋值的运算结果)
具体内容见代码:
#include<bits/stdc++.h>
using namespace std;
/*注意:
非:!
合取:&
析取:|
条件:-
双条件:+
命题字母小写
*/
const int N=1e4;
char s[N];//存放初始字符串
bool table[30];//标记命题变元是否存在
int explain[30];//存放每个命题变元的赋值(0或1)
int value[1000010];//存放每组赋值的最后运算结果
int sum=0;//下标
int youxian(char c){
switch(c){//定义运算符的优先顺序
case '#':return -1;
case '!':return 5;
case '&':return 4;
case '|':return 3;
case '-':return 2;
case '+':return 1;
case '(':return 0;
default:return 0;
}
}
void get_chars(){//将输入的字符串转换为逆波兰式
char post[N]={'\0'};int po=-1;//post存放转换后的命题形式,初始化为\0使strlen求长度时准确
char stack[N]={'#'};int st=0;//stack暂时存放运算符
int len=strlen(s);
for(int i=0;i<len;i++){//当该字符为命题字母时 ,直接存入post
if(s[i]>='a' && s[i]<='z'){
post[++po]=s[i];
continue;
}
if(s[i]=='!'||s[i]=='&'||s[i]=='|'||s[i]=='-'||s[i]=='+'){
/*下面一行包含两种情况,一是当前运算符优先级比上一个的小,则先把上一个运算符存入post,再把当前
运算符暂时存入stack,以便下次比较,二是两个运算符优先级相同,则按从左到右的顺序运算,操作和第一
种情况相同,还有一种运算符优先级大于上一个的情况,在60行得到了处理*/
while(youxian(s[i])<=youxian(stack[st])) post[++po]=stack[st--];
stack[++st]=s[i];
continue;
}
if(s[i]=='('){
stack[++st]=s[i];
continue;
}
if(s[i]==')'){
while(stack[st]!='(') post[++po]=stack[st--];//把括号之间的运算符加到post里
st--;//完成了一个括号内所有字符转换后,将st重新返回0,为后面的转换做准备
continue;
}
}
while(st) post[++po]=stack[st--];/*该操作主要处理运算符优先级大于上一个的情况,把之前存在stack里
的运算符一一存入post,至此,已完成全部字符串转换为逆波兰式的操作*/
strcpy(s,post);//由于post不是全局变量,所以需要复制给s
int l=strlen(s);
}
void settable(){//统计命题变元的个数
memset(table,0,sizeof(table));//将table数组初始化为0
int len=strlen(s);
for(int i=0;i<len;i++){
if(s[i]>='a'&&s[i]<='z') table[s[i]-'a']=true;//若含有某个变元,则将对应的table值变为1
}
for(int i=0;i<26;i++){
if(table[i]) sum++;//求命题变元的个数
}
sum=pow(2,sum);//一共2^ans个赋值情况
}
int boti(){//计算下标,如010表示2
int sum=0,wei=1;
for(int i=25;i>=0;i--){//从后往前依次成二倍相加,把二进制数转换为十进制数
if(table[i]){
if(explain[i]){
sum+=wei;/*expaain值为0时不需要加,只需加上1对应的值即可
如10010为1*2+1*2^4=20 */
} wei*=2;
}
}
return sum;//sum为最大情况个数
}
int cal(int a,int b,char c){//采用位运算对四种运算符进行操作
switch(c){
case'&':return a*b;//合取
case'|':if(a+b) return 1;else return 0;//析取
case'-':if(a==1 && b==0) return 0;else return 1;//条件,a为真,b为假时为0,其他都为1;
case'+':return !((a+b)&1);//按位运算,比如2的二进制为10,则选0&1为结果
}
}
int work(){//按照逆波兰式两两结合计算出最后结果
int stack[N],st=-1;
int len=strlen(s);
for(int i=0;i<len;i++){
if(s[i]>='a' && s[i]<='z'){
stack[++st]=explain[s[i]-'a'];//存入命题的一次赋值(为0或1)
continue;
}
if(s[i]=='!'){//是!时对上一个字符取非
stack[st]=(stack[st]+1)&1;//位运算:+1后再跟1进行与运算可实现非的效果
continue;
}
int ans=cal(stack[st-1],stack[st],s[i]);//两两结合运算
stack[--st]=ans;//每次将st归零 ,下次将stack[0]与stack[1]运算
}
return stack[0];//返回的是最终运算后的结果
}
void assign(){//计算一组赋值后的结果,如00010,10100对应的结果
int x=boti();
int ans=work();
value[x]=ans;
}
void generate(char c){//利用真值表列出所有的取值情况
while(c<='z'&&table[c-'a']==false) c++;//因为命题字母可以随意选择,所以要把26个遍历一遍
if(c>'z'){//超出z后再计算该组赋值的结果
assign();
return ;
}
explain[c-'a']=0;//类似树状图,遍历所有命题变元的0,1取值
generate(c+1);
explain[c-'a']=1;
generate(c+1);
}
void output1(){//输出析取范式
int i=0;
while(i<sum && !value[i]) i++;/*此处sum可理解为最大情况总数,
在generate函数中每组数据以sum为下标都有对应的value[sum]值
*/
if(i >= sum){
printf("无主析取范式\n");
return ;
}
printf("主析取范式为:m%d",i);
for(i++;i<sum;i++){
if(value[i]) printf(" V m%d",i);
}
printf("\n");
}
void output2(){//输出合取范式
int i=0;
while(i<sum && value[i]) i++;
if(i >= sum){
printf("无主合取范式\n");
return ;
}
printf("主合取范式为:M%d",i);
for(i++;i<sum;i++){
if(!value[i]) printf(" ∧ M%d",i);
}
printf("\n");
}
int main(){
cin>>s;
get_chars();
settable();
memset(value,0,sizeof(value));
memset(explain,0,sizeof(explain));
generate('a');//从a开始遍历26个字母
output1();
output2();
return 0;
}
测试样例如下: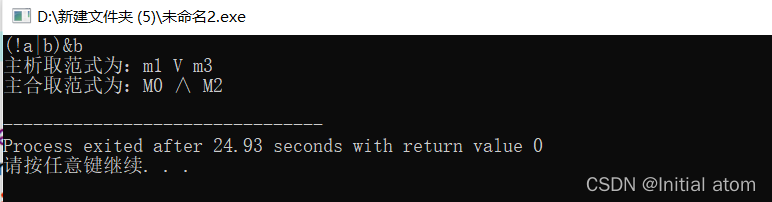





 本文详细介绍了如何使用C++编程实现离散数学中的主范式计算,包括非、合取、析取、条件和双条件等运算符的位运算实现,以及通过逆波兰表达式转换和真值表遍历来获取主析取范式和主合取范式的过程。
本文详细介绍了如何使用C++编程实现离散数学中的主范式计算,包括非、合取、析取、条件和双条件等运算符的位运算实现,以及通过逆波兰表达式转换和真值表遍历来获取主析取范式和主合取范式的过程。
















 459
459

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








