决策树公式推导

1. 决策树模型概述

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型：内部结点和叶结点。内部结点表示一个特征或属性，叶结点表示一个类。

决策树学习通常包括3 个步骤：特征选择、决策树的生成和决策树的修剪。决策树学习常用的算法有ID3 、C4.5 与CART。

2. 特征选择

决策树在一个分支时会从众多属性中选择一个属性进行划分，一般是选择最优的属性进行划分，对最优的评判需要依靠一些指标来进行。我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点“纯度”越来越高。

2.1 信息熵

在这之前，我们先定义信息熵的概念，假设样本集合 $D$ 中第 $k$ 类样本所占的比例为 $p_k(k=1,2,...,N)$ ，则 $D$ 的信息熵定义为
$$Ent(D)=-\sum _{k=1}^N{p}_{k}lo{g}_2{p}_k$$ $Ent(D)$ 的值越小，则 $D$ 的不确定性越高。

2.2 信息增益

假设离散属性 $a$ 有 $V$ 个可能的取值，若采用 $a$ 进行划分时，会产生 $V$ 个分支，每个分支包含了取值的所有样本，记其中一个分支为 $D^v$，可算出其信息熵，再考虑到每一个分支结点中的样本数不同，对其进行权重赋予 $|D^v|/|D|$，样本越多影响越大，所以属性 $a$ 对样本集 $D$ 划分的“信息增益”定义为
$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$$信息增益越大，则使用属性 $a$ 来进行划分所得的“纯度提升”越大，其中 $D$ 是要进行本次划分计算的集合。

2.3 增益率

信息增益对可取值数目较多的属性有一定的偏好，为了减少这种影响，可使用增益率来作为指标，增益率如下所示
$$Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}$$其中
$$IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|}$$称为属性 $a$ 的固有值。

增益率对属性可能取值少的属性比较有偏好，所以一般是先从候选属性中找出信息增益高于平均水平的属性，再从中选择增益率高的。

3. 决策树生成

3.1 ID3算法

ID3 算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树。具体方法是：从根结点开始，对结点计算所有可能的特征的信息增益， 选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一棵决策树。

ID3 算法只有树的生成，所以该算法生成的树容易产生过拟合。

具体例子在这里截取李航老师的《统计学习方法》来做理解：

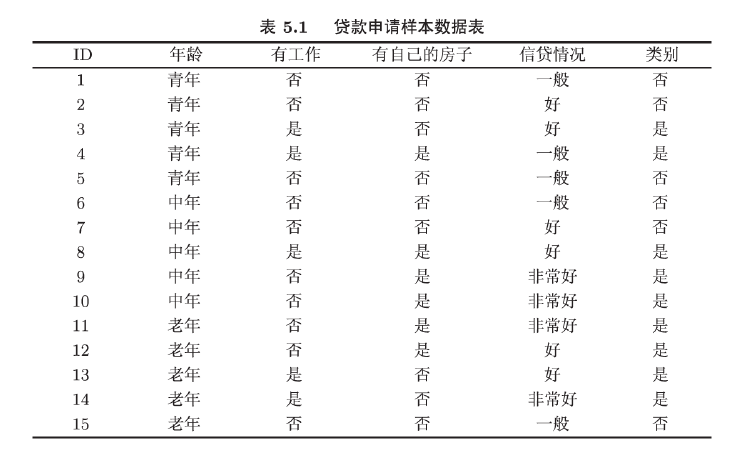
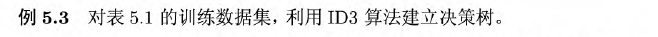
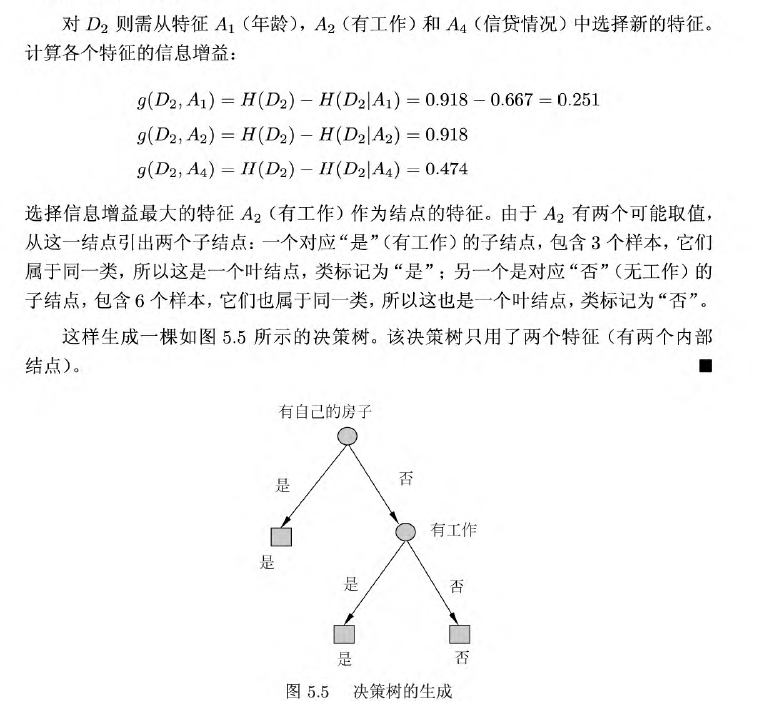
3.2 C4.5生成算法

C4.5 算法与ID3 算法相似， C4.5 算法对ID3 算法进行了改进。C4.5 在生成的过程中，用信息增益比来选择特征，除此之外没有不同

4. 决策树剪枝

决策树生成算法递归地产生决策树，直到不能继续下去为止。这样产生的树往往对训练数据的分类很准确，但对未知的测试数据的分类却没有那么准确，即出现过拟合现象。解决这个问题的办法是考虑决策树的复杂度，对已生成的决策树进行简化。

剪枝时可以按照类似正则化的方法对决策树进行剪枝。

设决策树 $T$ 的叶节点个数是 $|T|$ ，该叶节点有 $N_t$ 个样本点，其中 $k$ 的样本点有 $N_{tk}$ 个，$k=1,2,\cdots ,K$ ，$H_t(T)$ 为叶节点 $t$ 上的熵，$\alpha \ge 0$ 为参数，则决策树的损失函数定义如下：
$$C_{\alpha }(T)=\sum _{t=1}^{|T|}{N}_t{H}_t(T)+\alpha |T|$$其中熵为
H t ( T ) = − ∑ k N t k N t log ⁡ N t k N t H_t(T)=-\sum_k \frac{N_{tk}}{N_t} \log \frac{N_{tk}}{N_t} Ht​(T)=−k∑​Nt​N