数据结构（C）必会知识总结：绪论

绪论

一.怎样学数据结构？

牢记基本概念和经典算法
联系实际，富于联想
总结算法之间的共性和特性。
忌：求偏、求难、重算法轻概念。
三阶段：模仿->总结->创新

二.基本概念

1.数据分类
数据：信息的载体，是描述客观事物的数、字符及所有能输入到计算机中被计算 机程序识别和处理的符号的集合。
数值性数据
非数值性数据
数据元素：数据的基本单位
一个数据元素可由若干个数据项组成。
数据项是数据不可分割的最小单位。
数据对象：数据的子集。具有相同性质的数据元素集合。
例如：整数对象 N = { 0, 1, 2, … }
数据>数据元素>数据项

2.数据间的结构

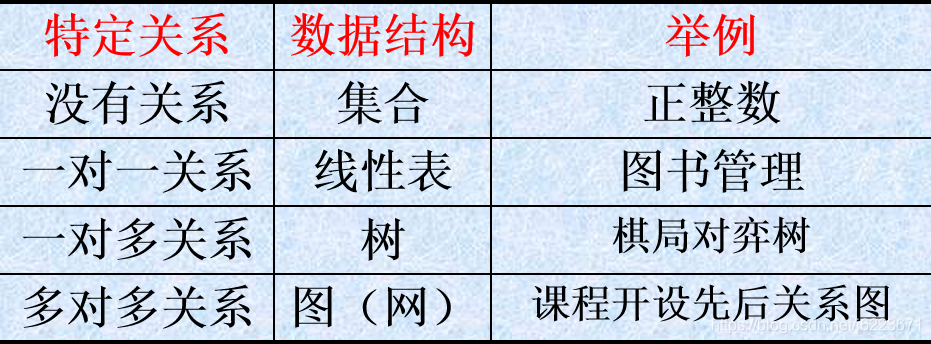
3.数据结构的形式
类似于代数系统，有限个的数据元素的集合+数据元素之间的关系（一种运算）
例：复数可定义为一种数据结构：
　　　COMPLEX=(C,R)
C：含有两个实数的集合{C1,C2}；
R：{P}是定义在C上的一种关系{<C1,C2>}
4.四种逻辑结构

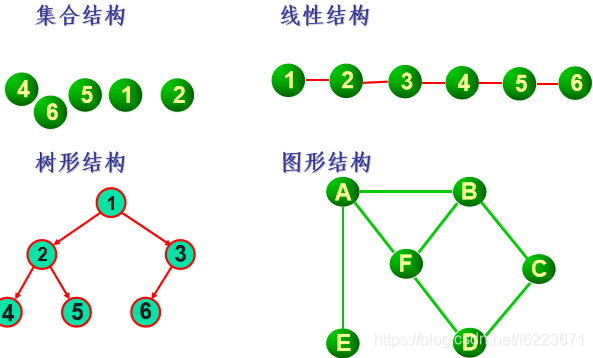
5.两种存储结构

顺序映象：借助元素在存储器的相对位置表示数据元素之间的逻辑关系。对应于顺序存储结构(sequential sets).
非顺序映象：利用指示元素存储地址的指针表示数据元素间的逻辑关系。对应于
链式存储结构(linked lists)
索引树(indexed trees)
散列表(hash tables)

6.算法特性
有穷性，确定性，能行性，一个或多个输出，零个或多个输入。
7.时间复杂度
算法的时间量度与问题的规模n有关
从算法中选取一种对于所研究问题来说是基本操作的原操作，以该基本操作重复执行次数作为算法的时间量度。
算法中基本操作重复执行次数是问题规模n的某个函数f(n)。
(渐近)时间复杂度：算法的时间量度记作T(n)=O(f(n))，表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称为算法的渐近时间复杂度，简称时间复杂度。
语句频度：语句重复执行的次数。

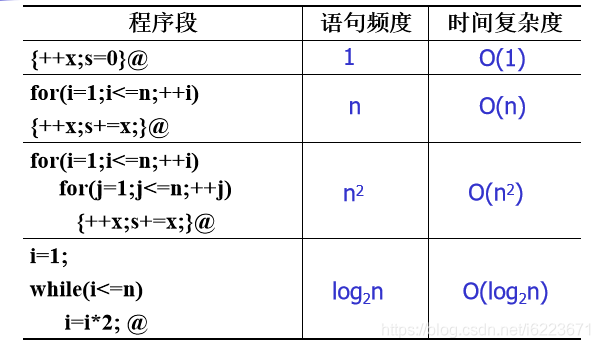
8.空间复杂度
渐进的空间复杂度：
算法所需存储空间的量度。记作：S(n)=O(g(n))，其中n为问题的规模,表示随着问题规模n的增大，算法运行所需存储量的增长率与g(n)的增长率相同。
算法的存储量包括:
1．输入数据所占空间;
2．程序本身所占空间；
3．额外辅助空间。