题解：CF1929F Sasha and the Wedding Binary Search Tree

题目大意

不多说，题面已经讲的很清楚了。

题目分析

我们可以发现题目给定的不是一个普通的二叉树，而是二叉搜索树。

考虑一个二叉搜索树的性质：

attribute：二叉搜索树的中序遍历序列是一个从小到大的序列。

同时 SGT 也是二叉搜索树的一种（二叉平衡树）。

所以我们考虑类似 SGT 的平衡操作，把_平衡树中序遍历，我们会得到一个从小到大的序列。我们以已知值为临界，可以得到若干组区间。具体的例子：

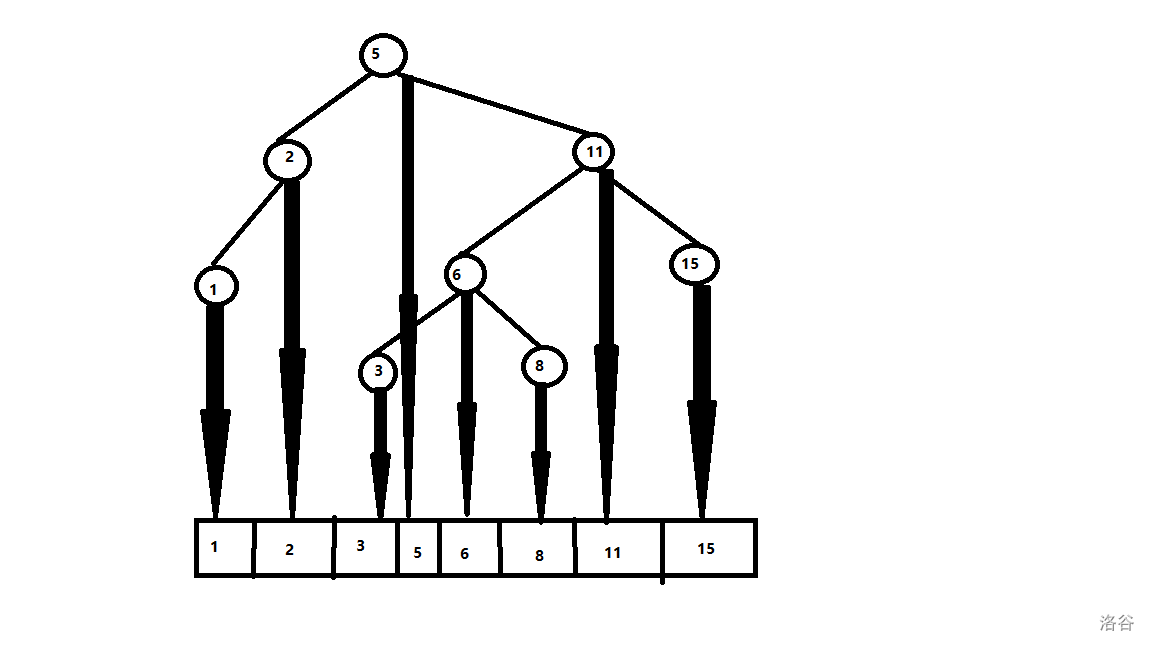
当然这里面是会有空的，而空的 $-1$ 会随机出现在各个地方。

因此我们认为如果把 $2$ 和 $3$ 替换为 $-1$，设 $C=21$，虽然 $2$ 和 $3$ 这一段与 $C$ 无关，我们可以发现这是一个固定的区间。

考虑推广方案，我们设这一段可填入值属于区间 $[l,r]$，显然化为插板法问题，最终可以通过大组合数计算法可得。

因此我们总结：

题目思路

main 思路

1. 求逆元用于计算组合数。
2. 接下来输入，进行 DFS 得到中序序列。
3. 直接插板计算得到答案。

求组合数思路

注：函数 $C_y^x$ 表示组合数。

假设我们现在要求 $C_y^x$ 的值。

1. 若 $x>y-x$，又公式 $C_y^x=C_y^{y-x}$，可优化为 $C_y^{y-x}$。
2. 此时逆元派上用场，具体方式如下——

int ans=1;
for(int i=y-x+1;i<=y;i++)ans=1ll*ans*i%mod;
for(int i=1;i<=x;i++)ans=1ll*ans*inv[i]%mod;

至此我们就完成了全部过程。

完结撒花！

接下来是大家期待的 AC 代码

#include<bits/stdc++.h>
#define NaOH(x,y) (C((x)+(y)-1,(y)-1)%mod)
using namespace std;
typedef long long ll;
const int MAXN=5e5,mod=998244353;
int n,CC;
int lson[MAXN+1],rson[MAXN+1],val[MAXN+1],inv[MAXN+1];
vector<int>order;
void init(void){
	inv[1]=1;
	for(int i=2;i<=MAXN;++i){
		inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
	}
	return;
}
void DFS(int u){
	if(u==-1)return;
	DFS(lson[u]);
	order.push_back(val[u]);
	DFS(rson[u]);
	return;
}
int C(int x,int y){
	if(x<y||y<0)return 0;
	if(y>x-y)return C(x,x-y);
	int t=1;
	for(int i=x-y+1;i<=x;i++)t=1ll*t*i%mod;
	for(int i=1;i<=y;i++)t=1ll*t*inv[i]%mod;
	return t;
}
void solve(void){
	order.resize(1);
	scanf("%d%d",&n,&CC);
	for(int i=1;i<=n;i++){
		scanf("%d%d%d",lson+i,rson+i,val+i);
	}
	DFS(1);
	int lst,ans;
	lst=ans=1;
	int d=1;
	for(int i=1;i<=n;i++){
		if(order[i]!=-1){
			ans=1ll*ans*NaOH(i-lst,order[i]-d+1)%mod;
			d=order[i];lst=i+1;
		}
	}
	ans=1ll*ans*NaOH(n+1-lst,CC-d+1)%mod;
	printf("%d\n",ans);
	return;
}
int main(){
	init();
	int T;scanf("%d",&T);
	while(T--)solve();
	return 0;
}