二、求解已经因式分解的矩阵的线性方程组
- 容易求解的线性方程组
- 因式分解求解方法
容易求解的线性方程组
先讨论矩阵A是n维可逆矩阵的情况,即
对角矩阵
假设A是非奇异对角矩阵,线性方程组Ax=b可以写成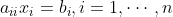 ,方程组的解为
,方程组的解为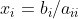 ,即经过n次浮点运算即可。
,即经过n次浮点运算即可。
下三角矩阵
矩阵A是n维非奇异下三角矩阵:即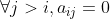 ,下三角矩阵非奇异的充要条件是对所有的i成立
,下三角矩阵非奇异的充要条件是对所有的i成立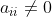 。
。
此时Ax=b可以写成:
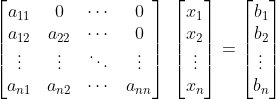
可推出:
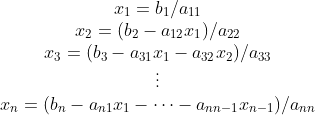
共需要的计算次数: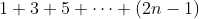 ,即为等差数列前n项和,
,即为等差数列前n项和,
上三角矩阵
矩阵A是非奇异上三角矩阵,即 是非奇异下三角矩阵,Ax=b可以写成:
是非奇异下三角矩阵,Ax=b可以写成:
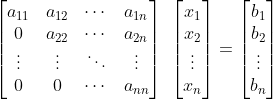
可推出:
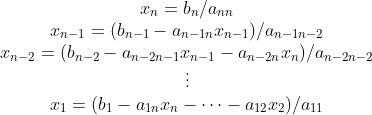
跟下三角矩阵同理,需要 次计算。
次计算。
正交矩阵
矩阵A为正交矩阵的条件是,求解
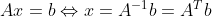 ,即计算
,即计算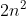 次。
次。
如果A具有特殊结构,也可以减少计算量,比如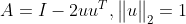 ,此时
,此时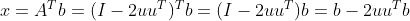 ,只需要4n次计算。
,只需要4n次计算。
排列矩阵
令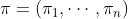 为
为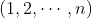 的一种排列,相应的排列矩阵
的一种排列,相应的排列矩阵 定义为:
定义为:
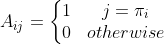
排列矩阵的每行(每列)只有一个元素等于1,所有其他元素都为0。排列矩阵的逆矩阵就是逆排列对应的排列矩阵。实际上就是 ,而与1相乘不需要运算。该排列矩阵的方程组的求解需要0个运算。
,而与1相乘不需要运算。该排列矩阵的方程组的求解需要0个运算。
因式分解求解算法
将A表示为一系列非奇异矩阵的乘积,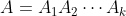 ,
, ,可推出:
,可推出:
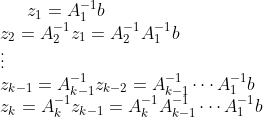
可以通过这种方法求解:

求解多个右边项的方程组
考虑求解方程组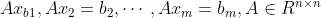 是非奇异矩阵,将方程组等价于计算矩阵
是非奇异矩阵,将方程组等价于计算矩阵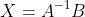 ,其中
,其中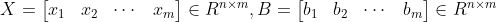
求解先对A进行因式分解,成本为f,然后对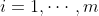 通过过求解步骤计算
通过过求解步骤计算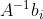 ,总计算量是f+ms。
,总计算量是f+ms。
来源:https://blog.youkuaiyun.com/wangchy29/article/details/87903699








 本文主要探讨求解已因式分解的矩阵的线性方程组。先讨论了矩阵A为可逆矩阵时,对角、下三角、上三角、正交、排列矩阵等容易求解的线性方程组的解法及计算次数,接着介绍因式分解求解算法,还提及求解多个右边项方程组的方法及总计算量。
本文主要探讨求解已因式分解的矩阵的线性方程组。先讨论了矩阵A为可逆矩阵时,对角、下三角、上三角、正交、排列矩阵等容易求解的线性方程组的解法及计算次数,接着介绍因式分解求解算法,还提及求解多个右边项方程组的方法及总计算量。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








