题目描述
题目分析
显然，这是一道最短路径的题目，我们可以选择 D i j k s t r a Dijkstra Dijkstra 算法求解。但是，题目中有 他们可以免费在最多 k 种航线上搭乘飞机。也就是说，我们可以令最多 k k k 条边的权值为零。这时，我们就要采用分层图。
分层图
分层图并不是算法，而是一种建模思想。建模后，依然是用 D i j k s t r a Dijkstra Dijkstra 求解，与单纯的最短路径问题没有区别。接下来，通过一个例子来了解分层图。
假设有一张 4 4 4 个顶点、 4 4 4 条边的无向图， k = 1 k = 1 k=1。
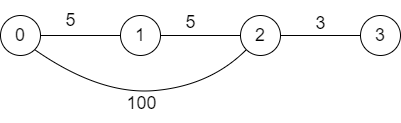
k = 1 k = 1 k=1 表明我们可以令某一条边的权值为0，换句话来说，就是为某条边添上一条权值为0的重边。因为每一条边都有可能被选到，所以图中的每一条边都应该有一条这样的重边。但是，如果我们将重边直接添在原图上，就只能表示一次选择（某条边的权值为0）。所以，我们要创建原图的副本，要做 k k k 次选择，就要创建 k k k 张副本，连同原图共 k + 1 k + 1 k+1 层图。每层图之间依靠权值为0的重边连接。每次进入下一层图，就是做了一次选择。
为了与原图有区别，我们需要对副本的顶点按顺序重新编号。原图有 n n n 个顶点，建图后就变成了 ( k + 1 ) n (k + 1)n (k+1)n 个。此时，边 e ( u , v ) e(u, v) e(u,v) （一层图共 n n n 个顶点，且是无向图）的到下一层图的重边就变成了 e ( u , v + n ) e(u, v + n) e(u,v+n) 和 e ( v , u + n ) e(v, u + n) e(v,u+n) 。我们要找到
最低0.47元/天 解锁文章
扫一扫
500
到【灌水乐园】发言
