奇异值分解（SVD）

目录

奇异值分解

数据线性变换

拉伸

旋转

物理意义

SVD推广到任意大小矩阵

SVD分解时空矩阵​编辑

如何求SVD分解 ​编辑

求解SVD分解的步骤

PCA的主成分与SVD的关系

非负矩阵分解

---

奇异值分解

数据线性变换

拉伸

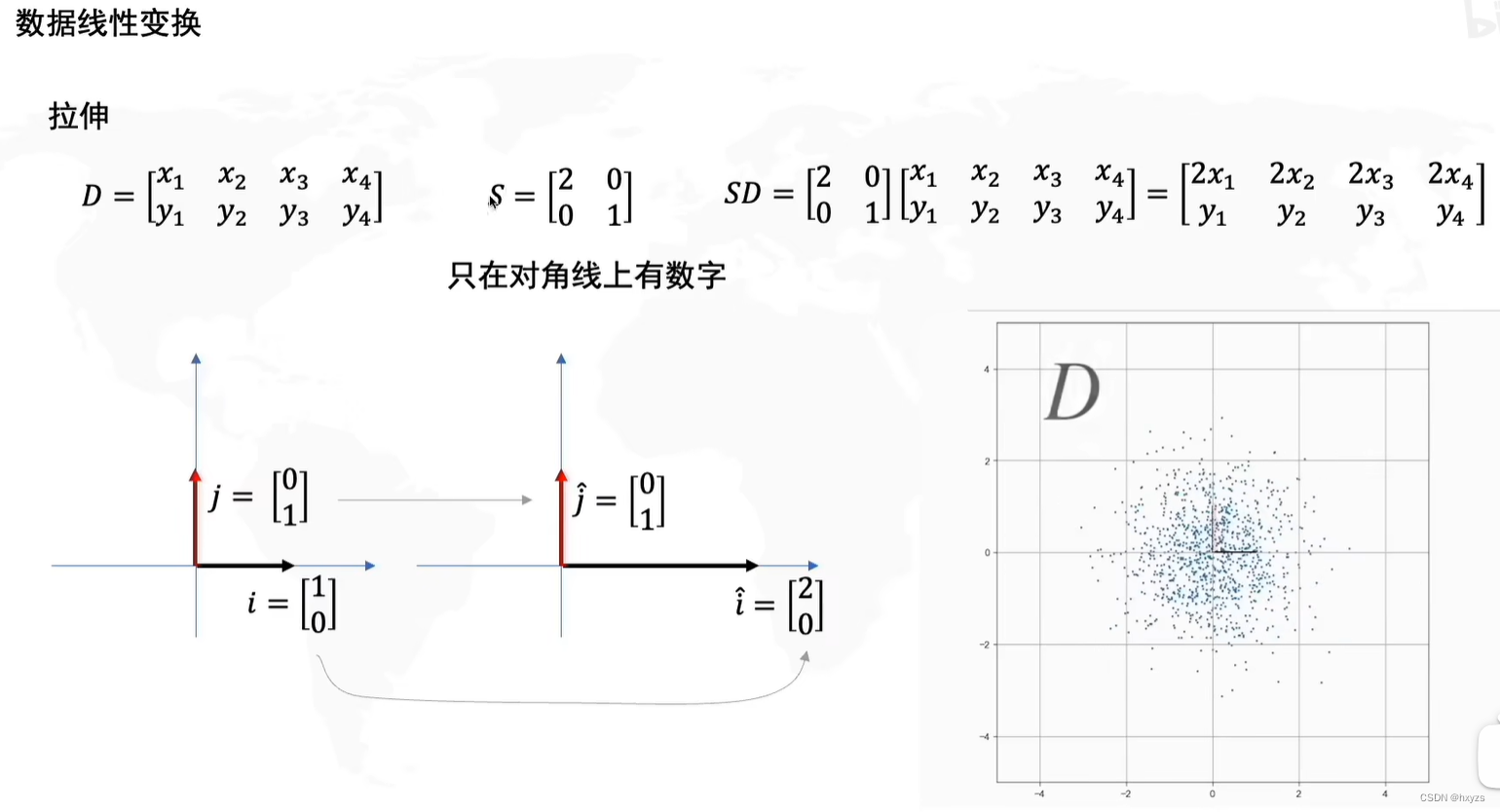
特点：变换的矩阵是对角阵！

旋转

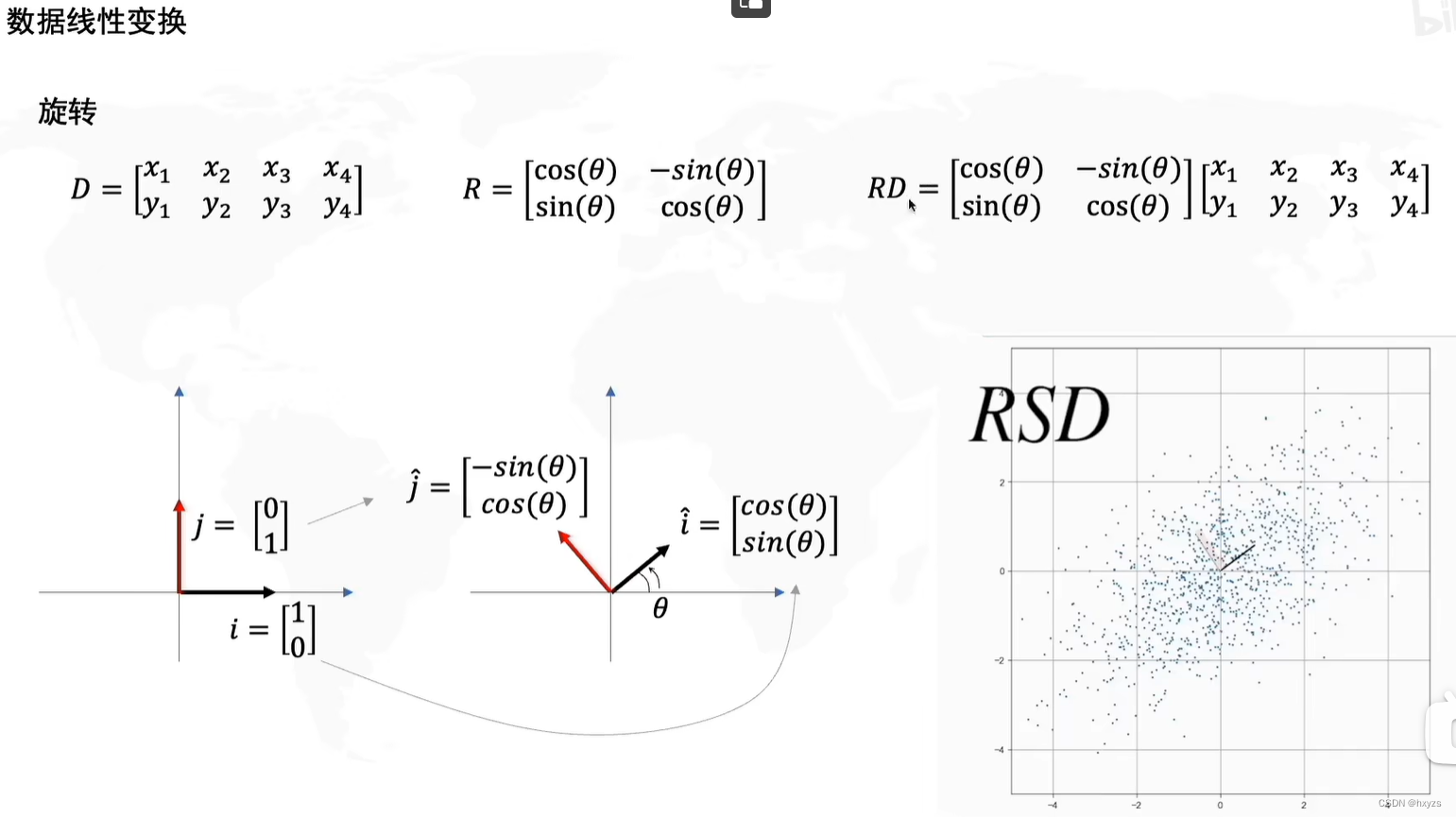
 特点：变换的矩阵是正交矩阵！

 注意：如果矩阵是一个正交矩阵（AxA^T=E），那么其内部蕴含的几何意义是旋转;如果矩阵是一个对角矩阵，那么其内部蕴含的几何意义是拉伸！

实质：先进行旋转-->再进行拉伸-->最后再进行旋转回来！

物理意义

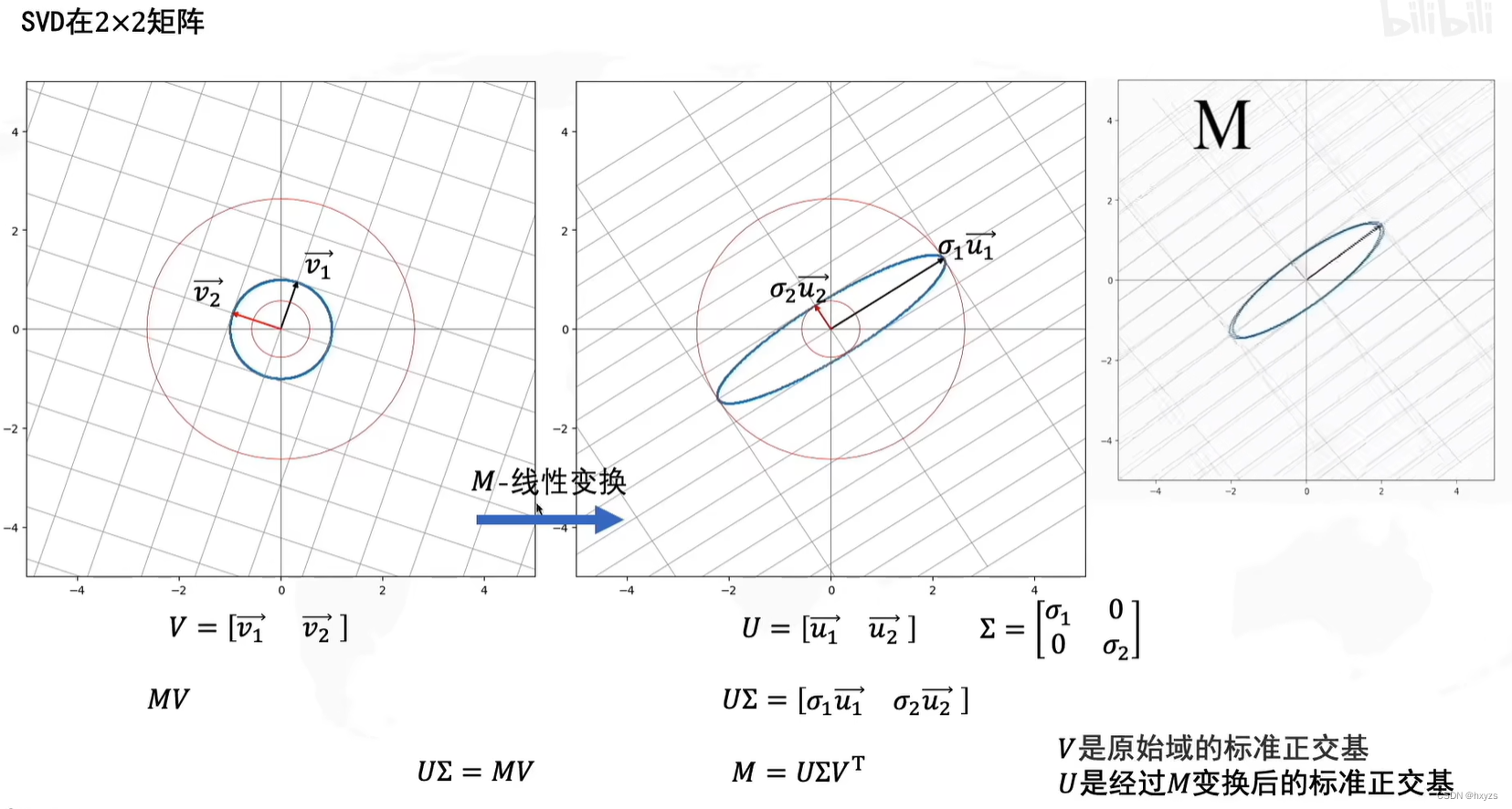
 物理意义：在变换前找到一组正交基V，目的是找到变换之后的正交基U！

SVD推广到任意大小矩阵

 注意：这五个奇异值代表的是五个基，且基的重要程度从上往下依次降低！

注意：这里是去掉不重要的特征值！

 SVD分解时空矩阵

 

如何求SVD分解 

 

 

 

 

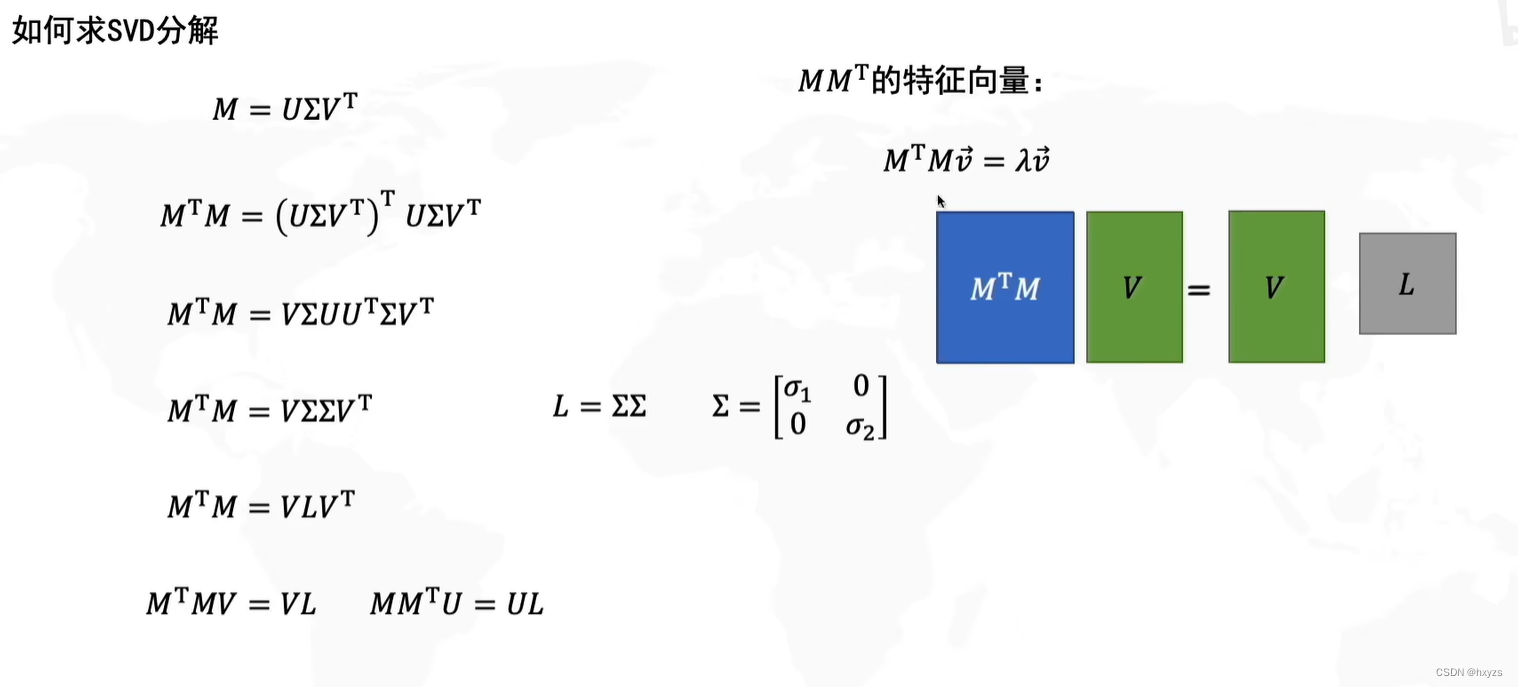
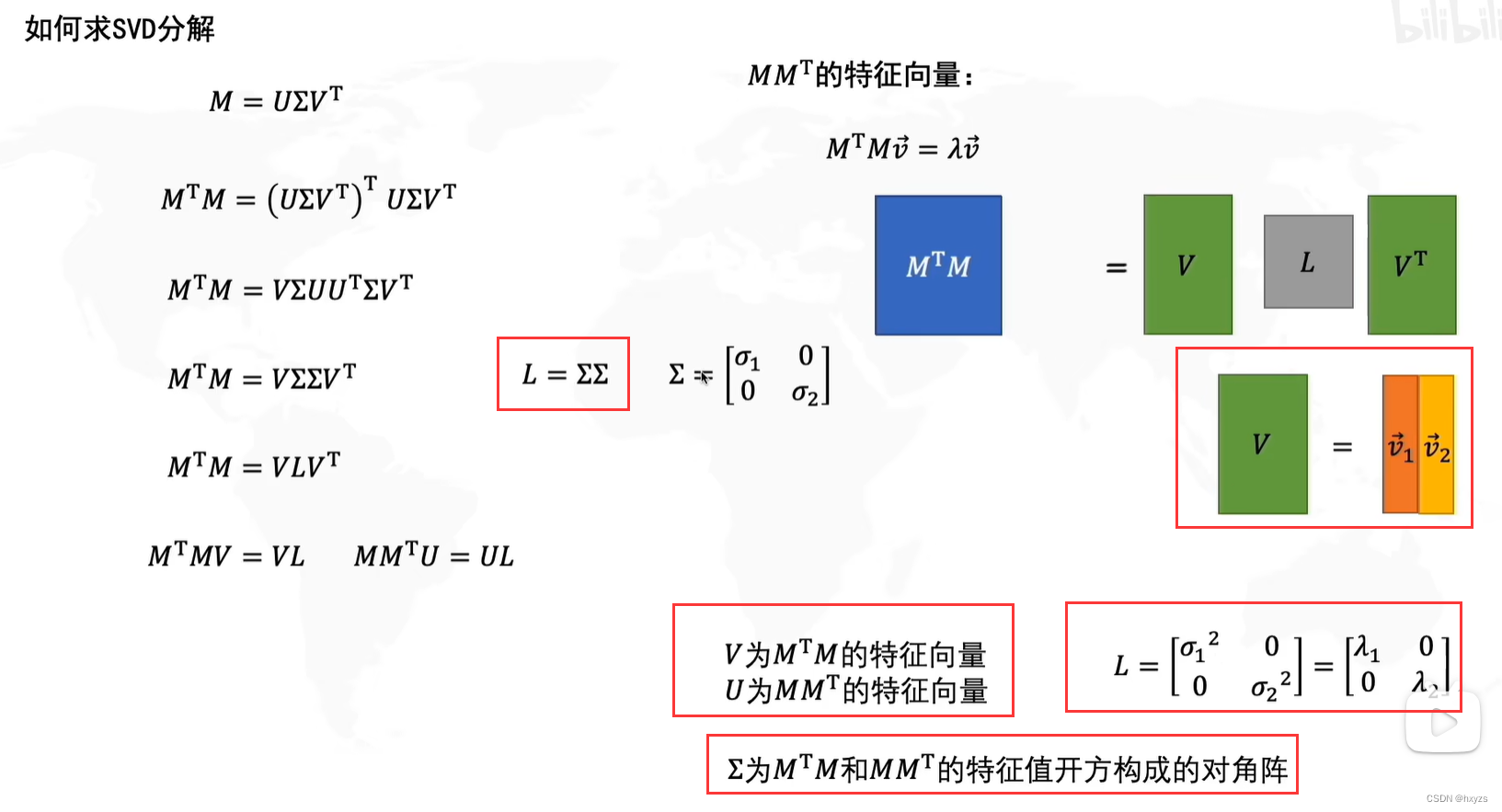
 求解SVD分解的步骤

 PCA的主成分与SVD的关系

 非负矩阵分解

 注意：矩阵中的元素全部为正，方便分析物理意义！S矩阵的列代表空间，B矩阵的行代表时间！因为没有协方差矩阵所以很难说明三种成分中哪个是主要的！