《归并排序》的思想以及代码实现--排序算法（六）

本文链接：https://blog.youkuaiyun.com/hwh295/article/details/109509819

文章目录

前言
- 1.排序算法的分类
一、（MERGE SORT）的基本概念
四、排序算法情况

前言

1.排序算法的分类

内部排序:
指将需要处理的所有数据都加载到内部存储器(内存)中进行排序。
外部排序法：
数据量过大，无法全部加载到内存中，需要借助外部存储(文件等)进行排序。
常见的排序算法分类

一、（MERGE SORT）的基本概念

1.基本介绍

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修
补"在一起，即分而治之)。

2.执行逻辑

归并的执行逻辑：

分：
- 首先得到数组下标中位数，按中位数进行划分出两个数组。按这个思路递归划分，最后得到多个只有一个数的数组，即不能再分。
治：
- 把这些数经过有序的排列进行合并，变成有序的数组。

3.图解过程

步骤：
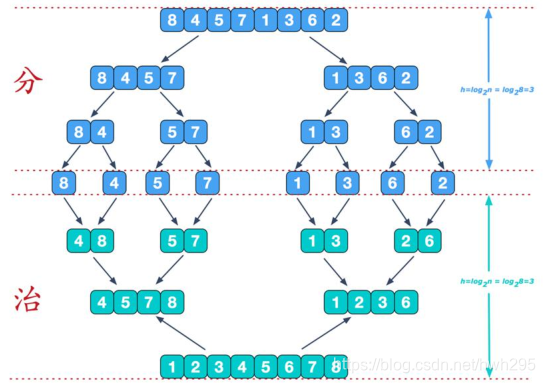
在这里插入图片描述

动态图：
在这里插入图片描述

4.代码实现

package com.datastructure.sort;

import java.util.Arrays;

/**
 * @author Hacah
 * @date 2020/10/28 20:54
 */
public class MergetSort {

    public static void main(String[] args) {
        int[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
        int[] tempArr = new int[arr.length];
        merget(arr, 0, arr.length - 1, tempArr);
        System.out.println(Arrays.toString(arr));
    }

    /**
     * @param arr   排序的数组
     * @param left  数组的最左的下标
     * @param right 数组最右的下标
     */
    public static void merget(int[] arr, int left, int right, int[] tempArr) {
        if (left < right) {
            int mid = (left+right) / 2;
            merget(arr, left, mid, tempArr);
            merget(arr, mid + 1, right, tempArr);
            arrMerget(arr, left, mid, right, tempArr);
        }
    }

    /**
     * 合并的方法，把两个数组排序合并
     *
     * @param arr     排序的数组
     * @param left    数组最左边的下标
     * @param mid     数组中间的下标
     * @param right   数组最右边的下标
     * @param tempArr 一个临时的数组
     */
    public static void arrMerget(int[] arr, int left, int mid, int right, int[] tempArr) {
        // 一个数组的开始索引
        int first = left;
        // 另一个数组的开始索引
        int first2 = mid + 1;
        // 声明临时数组的索引
        int tempArrIndex = 0;


        // 把两个数组的数据按序放到临时数组，直到有一个数组的数据全部放过去了。
        while (first <= mid && first2 <= right) {
            if (arr[first] <= arr[first2]) {
                tempArr[tempArrIndex] = arr[first];
                tempArrIndex++;
                first++;
            } else {
                tempArr[tempArrIndex] = arr[first2];
                tempArrIndex++;
                first2++;
            }

        }

        // 把剩下一个数组中还有的数组也放到临时的数组中
        while (first <= mid) {
            tempArr[tempArrIndex] = arr[first];
            tempArrIndex++;
            first++;
        }
        while (first2 <= right) {
            tempArr[tempArrIndex] = arr[first2];
            tempArrIndex++;
            first2++;
        }

        // 把临时数组的数据复制到原数组中
        // 初始化索引
        tempArrIndex = 0;
        int tempLeft = left;
        while (tempLeft <= right) {
            arr[tempLeft] = tempArr[tempArrIndex];
            tempArrIndex++;
            tempLeft++;
        }


    }
}