北大郭炜程序设计算法二：汉诺塔问题

最新推荐文章于 2021-08-25 12:09:29 发布

云之声759

最新推荐文章于 2021-08-25 12:09:29 发布

阅读量509

点赞数

CC 4.0 BY-SA版权

分类专栏： MOOC练题 Python 文章标签：递归

本文链接：https://blog.youkuaiyun.com/huitinfeng/article/details/96749522

本文介绍了汉诺塔问题，一个涉及到递归的经典问题。内容包括问题背景、递归作用的三点阐述，以及解决汉诺塔问题的递归思路和基本步骤。通过将大盘子分解为小规模子问题，逐步移动盘子达到目标位置。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

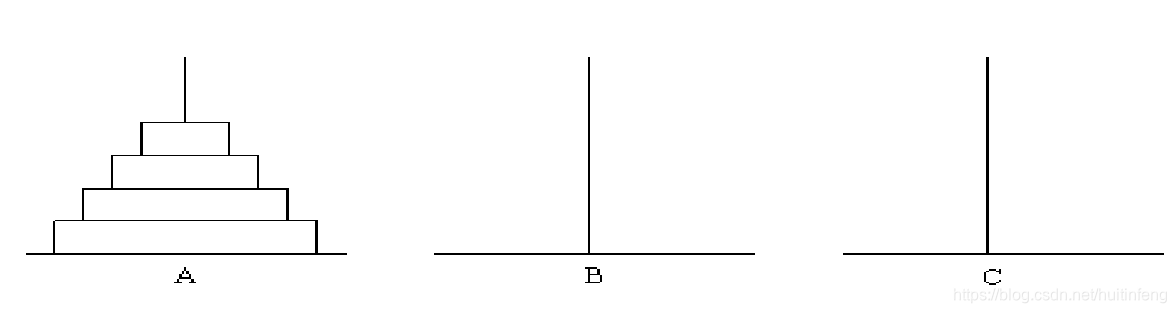
古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小不等，大的在下，小的在上（如图所示）。有一个和尚想把这64个盘子从A座移到C座，但每次只能允许移动一个盘子，并且在移动的过程中，3个座上的盘子始终保持大盘在下，小盘在上。在移动的过程中，可以利用B座，要求输出移动的步骤。

递归的作用：

1）替代多重循环；

2）解决本来就是用递归形式定义的问题；

3）将问题分解成为规模更小的子问题进行求解；......

解析思路如下：

如果有三个盘子a（小）,b（中）,c（大），都在第一根柱子上。则先把a移到第三根柱子上，然后把b移到第二根柱子上，再把a移到第二根柱子上（此时第三根柱子已经空了）；然后再将第一根柱子上的c移到第三根柱子上，再把第二根柱子上的上面的小的a移到第一根柱子上，接着将第二根柱子上的b移到第三根柱子上，第一根柱子上的a移到第三根柱子上就完成了，依然是a在上，b在中，c在下，并且过程中一次仅移动一个。如果盘子更多，以此递推就好。

代码如下：

#include <iostream>
#include <cstdio>
using namespace std;

void Hanoi(int n ,char src ,char mid ,char dest )
//将src座上的n个盘子，以mid座为中转，移动到dest座
{
	if( n == 1 ){//只需移动一个盘子 
		cout << src << "->" << dest << endl ;
		//直接将盘子从src