LeetCode 63 不同路径II（动态规划）_动态规划求路径力扣63-优快云博客

本文链接：https://blog.youkuaiyun.com/huihui_8/article/details/104473756

本文探讨了在存在障碍物的网格中寻找从左上角到右下角的不同路径数量的问题。通过动态规划方法，详细解析了算法实现过程，包括状态定义、初始化及递推方程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 题目链接

https://leetcode-cn.com/problems/unique-paths-ii/

2. 题目描述

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

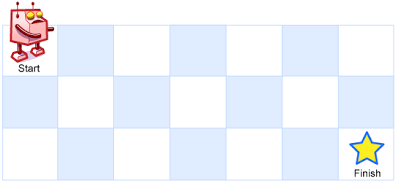
网格中的障碍物和空位置分别用 1 和 0 来表示。

说明：m 和 n 的值均不超过 100。

示例 1:
输入:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]

输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

3. 题目解析

1) 拆解问题

和Leetcode 62相同，每次移动只能是向下或者向右移动一步

2) 定义状态

从起点到达该位置总共有多少条不同的路径

3) 状态数组初始化

对于列，当前有障碍物时dp[i][0] = 0，否则dp[i][0] = dp[i - 1][0];每行状态数组初始化情况类似

4) 递推方程

当前位置有障碍物时，dp[i][j] = 0;否则从上边或者左边到达

dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

4. 代码实现

int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize){
    int n = obstacleGridColSize[0];
    int m = obstacleGridSize;
    
    if (obstacleGrid[0][0] == 1)
        return 0;
    long dp[m][n];
    dp[0][0] = 1;

    for (int i = 1; i < m; ++i) {
        if (obstacleGrid[i][0] == 1)    //有障碍物，状态数组为0
            dp[i][0] = 0;
        else
            dp[i][0] = dp[i - 1][0];
    }
    for (int i = 1; i < n; ++i) {
        if (obstacleGrid[0][i] == 1)    //有障碍物，状态数组为0
            dp[0][i] = 0;
        else
            dp[0][i] = dp[0][i - 1];
    }

    for (int i = 1; i < m; ++i) {
        for (int j = 1; j < n; ++j) {
            if (obstacleGrid[i][j] == 1)    //有障碍物，状态数组为0
                dp[i][j] = 0;
            else
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; 
        }
    }
    //printf("m = %d, n = %d", m ,n);
    return dp[m - 1][n - 1]; 
}

5. 提交记录