快速排序复杂度证明 及优化

快排是分治的思想，分解成小问题，解决(排序)，合并(排序过程都是在一个数组上直接操作，不用合并的过程)。

快速排序复杂度

最坏情况(O(n^2))

证明：最坏情况下就是对已经排好序的序列操作，假设是从小到大，那么last就会从最后一直比到first(哨兵位置)(共比较n-1次)，并且将序列分为1和n-1，之后n-1以类似方式被递归划分。

假设算法每次都进行了这种不对称划分，划分的时间代价为θ(n)[//n是元素个数]，因为对一个大小为0的数组递归调用后T(0)=θ(1)[//相当于只调用一次就会返回，不会进行更深层次的递归调用],算法的运行时间可以递归表示为：

 T(n)=T(n-1)+T(0)+θ(n)=T(n-1)+θ(n)

书上说是用代换法。代换法两步：1)假设解的形式  2)用数学归纳找出使解真正有效的常数。例如：

链接  (这个证明有错误)总的过程就是先根据经验猜测，然后代入推导。

此处证明：链接：

所以T(n)=θ(n^2). 快速排序在最坏情况下的 运行时间是θ(n^2).最坏情况下并不比直接插入好。

最好情况(O(nlgn))

最好情况是在平均划分的情况下：

T(n)≤2T(n/2)+θ(n).

之所以是≤，是因为一个被划分为n/2取地板，另一个子问题大小为n/2取天棚减1.

这个使用主定理（the Master Theorem）方法证明：

主定理：

//主变量定理证明我没看。

在T(n)≤2T(n/2)+θ(n)中，f(n)=θ(n)=cn.  a=2,b=2,所以使用第2条得T(n)=O(nlgn).

还讨论了，划分是9:1划分，得到的结果是运行时间也是θ(nlgn).主要原因是任意一种常数比例进行的划分都会产生深度为θ(lgn)得递归树。

平均情况θ(nlgn)

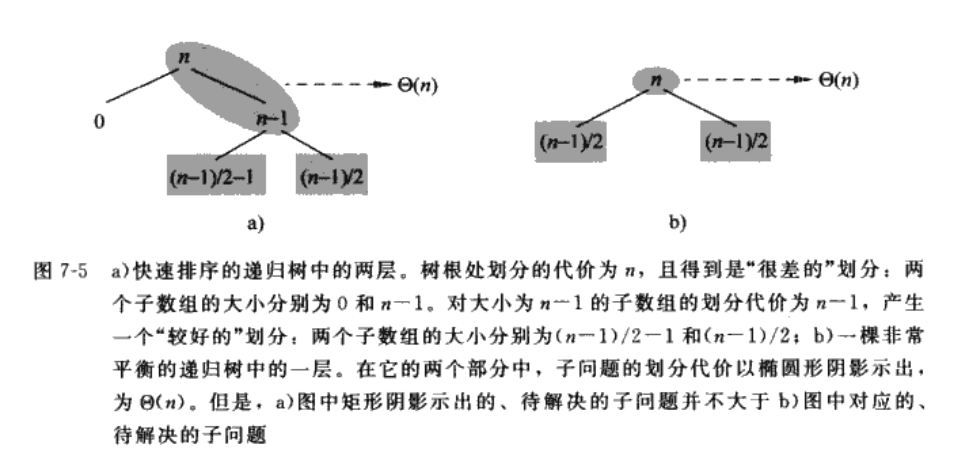
在平均情况下，好的划分和坏的划分是平均出现在划分树上的，当好、差划分交替在各层时，快排的运行时间就如全是好的划分一样，为θ(nlgn).

附知乎大佬回答：

//这个平均情况的公式不太理解

优化

//明天再来写，根据规模使用不同的排序算法+快排变形。

参考：百度百科+《算法导论》