红黑树详解：平衡二叉查找树的实战应用与操作-优快云博客

本文链接：https://blog.youkuaiyun.com/huangwen001/article/details/119799167

一、红黑树为什么会出现呢？

是因为二叉搜索树有可能会出现极端的情况，就是只有一侧有数据，那这样的话就会降级为链表。后来出现了平衡二叉树，但是由于强制平衡所导致付出的代价比较高昂，所以黑红树出现了。

二、简介

红黑树（Red Black Tree）的实现是基于二叉查找树的，对于含有n个节点的二叉查找树的最坏的情况是这n个节点形成一条单链，此时二叉查找树的高度为n，时间复杂度为O(n)。为了维持O(lg n)的运行时间，就需要采取一些措施在不影响二叉查找树的性质下改变二叉查找树的结构，使之平衡。红黑树就是这样一种二叉查找树，即自平衡二叉查找树。

三、特征

红黑树是每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色。
性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3. 所有叶子都是黑色。（叶子是NUIL节点）
性质4. 每个红色节点的两个子节点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色节点）
性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

在这里插入图片描述

四、代码

然后我们看一下节点的定义

public class RBTNode<T extends Comparable<T>> {
        boolean color;        // 颜色
        T key;                // 关键字(键值)
        RBTNode<T> left;    // 左孩子
        RBTNode<T> right;    // 右孩子
        RBTNode<T> parent;    // 父结点
 
        public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) {
            this.key = key;
            this.color = color;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }
 
    }

当对红黑树进行插入或删除时，就有可能破坏红黑树的性质，这时需要通过变色、左旋与右旋操作平衡红黑树。变色操作很简单，红变黑，黑变红，就不仔细介绍了，下面介绍左旋与右旋

左旋

此图是以X为旋转结点

定义：以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。

/* 
 1. 对红黑树的节点(x)进行左旋转
 2.  3. 左旋示意图(对节点x进行左旋)：
 4.      px                              px
 5.     /                               /
 6.    x                               y                
 7.   /  \      --(左旋)-.           / \                #
 8.  lx   y                          x  ry     
 9.     /   \                       /  \
 10.    ly   ry                     lx  ly  
 11.  12.  */
private void leftRotate(RBTNode<T> x) {
    // 设置x的右孩子为y
    RBTNode<T> y = x.right;
 
    // 将 “y的左孩子” 设为 “x的右孩子”；
    // 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”
    x.right = y.left;
    if (y.left != null)
        y.left.parent = x;
 
    // 将 “x的父亲” 设为 “y的父亲”
    y.parent = x.parent;
 
    if (x.parent == null) {
        this.mRoot = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点
    } else {
        if (x.parent.left == x)
            x.parent.left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
        else
            x.parent.right = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
    }
    
    // 将 “x” 设为 “y的左孩子”
    y.left = x;
    // 将 “x的父节点” 设为 “y”
    x.parent = y;
}

右旋

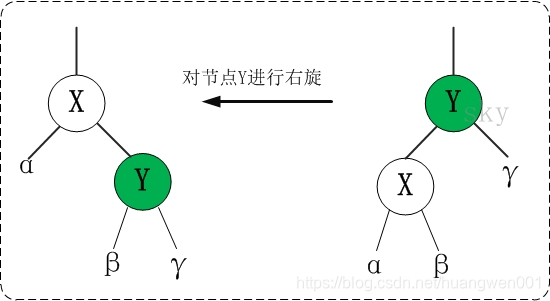
此图是以Y结点为旋转结点

定义：以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。

/* 
 * 对红黑树的节点(y)进行右旋转
 *
 * 右旋示意图(对节点y进行左旋)：
 *            py                               py
 *           /                                /
 *          y                                x                  
 *         /  \      --(右旋)-.            /  \                     #
 *        x   ry                           lx   y  
 *       / \                                   / \                   #
 *      lx  rx                                rx  ry
 * 
 */
private void rightRotate(RBTNode<T> y) {
    // 设置x是当前节点的左孩子。
    RBTNode<T> x = y.left;
 
    // 将 “x的右孩子” 设为 “y的左孩子”；
    // 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”
    y.left = x.right;
    if (x.right != null)
        x.right.parent = y;
 
    // 将 “y的父亲” 设为 “x的父亲”
    x.parent = y.parent;
 
    if (y.parent == null) {
        this.mRoot = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点
    } else {
        if (y == y.parent.right)
            y.parent.right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”
        else
            y.parent.left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
    }
 
    // 将 “y” 设为 “x的右孩子”
    x.right = y;
 
    // 将 “y的父节点” 设为 “x”
    y.parent = x;
}

五、插入情况分析

红黑树的插入和搜索二叉树一样，都需要先找到其插入位置。
插入的节点默认是红色。（要是黑色的话，那所有性质都一直满足，皆大欢喜了，就不用再平衡了，肯定不对）
然后再通过变色、左旋、右旋等满足其性质。
在这里插入图片描述

在这里插入图片描述

1. 被插入的节点是根节点。
处理方法：直接把此节点涂为黑色。

2. 被插入的节点的父节点是黑色。
处理方法：什么也不需要做。节点被插入后，仍然满足红黑树性质。

3. 被插入的节点的父节点是红色。
处理方法：这种情况下有连续两个红色节点，不满足红黑树的性质，需要调整。简单分析一下，被插入节点的父节点是红色，那么其祖父节点肯定存在且一定是黑色。我们依据其叔叔节点（其父亲节点的兄弟节点）的情况，将这种情况进一步划分。

3.1 叔叔结点为红色
我们可以将父亲结点p和叔叔结点s变黑色，祖父结点变红色就能解决问题。但是只是局部的平衡，祖父结点变红色还可能引起不平衡，因此还需要将祖父结点pp作为插入结点继续向上的平衡。(如果pp的父节点为空则直接把pp变黑色)

把祖父结点pp变红色
把父结点p和叔叔结点变黑色
把pp作为新的插入结点

3.2 插入结点的父结点p是祖父结点pp的左子结点，插入结点的叔叔结点s不存在或为黑色
这里可能会有疑问：既然父结点为红，为什么叔叔结点会为黑色，这样叔叔结点所在子树的黑色结点数目不就多一了吗?
答：因为类似于上述3.1向上平衡的情况，因此插入结点的叔叔结点有可能是黑色的。

这种情况意味着左边子树结点比右边少，我们就需要通过右旋向右子树去借节点。

3.2.1 插入结点是父结点p的左子结点
因为把pp右旋后是黑色破坏了黑色结点的数量，因此还需要将pp变红。p则需要变为原来pp的颜色，即黑色。

对pp右旋
p变黑，pp变红

3.2.2 插入结点是父结点p的右子结点
这种情况我们发现对插入结点的父结点p进行左旋，就变成情况3.2.1了，然后按照3.2.1进行处理

对p左旋
转到情况3.2.1处理

3.3 插入结点的父结点p是祖父结点pp的右子结点，插入结点的叔叔结点s不存在或为黑色
这种情况就是3.2情况的对称情况，这里有一个小技巧,把3.2的情况的左右对换就是3.3情况了

3.3.1插入结点是父结点p的右子结点
这种情况和3.2.1类似，因为是对称的，只要把左变成右，右变成左就行了。
对pp左旋
p变黑，pp变红

3.3.2插入结点是父结点p的左子结点
这种情况是和3.2.2类似，我们对p右旋，转为情况3.3.1
对p右旋
转到情况3.3.1处理

代码就不贴出来了，有兴趣大家可以看 jdk8 HashMap的源码