从0开始RSA 逐步变成高手(四) 密钥基础

 公钥私钥生成代码

#公钥密钥生成
from Crypto.PublicKey import RSA
import libnum
import gmpy2
p = libnum.generate_prime(1024)
q = gmpy2.next_prime(p)
n = p * q
e = 65537
phi_n = (p-1) * (q-1)
d = gmpy2.invert(e, phi_n)
#生成公钥
rsa_components = (int(n), int(e))
keypair = RSA.construct(rsa_components)
with open('pubckey.pem', 'wb') as f:
    f.write(keypair.exportKey())


#生成私钥
rsa_components = (int(n), int(e), int(d))
keypair = RSA.construct(rsa_components)
with open('privkey.pem', 'wb') as f:
    f.write(keypair.exportKey())

运行之后会生成一个公钥，一个密钥。

读取方式

from Crypto.PublicKey import RSA

# 读取公钥 公钥可以读取出n和e
with open('pubckey.pem', 'rb') as f:
    key = RSA.import_key(f.read())     #读取方式
    print(f"n ={key.n}")
    print(f"e ={key.e}")

# 读取私钥 私钥可以读取出n、e、d、p、q
with open('privkey.pem', 'rb') as f:
    key = RSA.import_key(f.read())    #读取方式
    print(f"n ={key.n}")
    print(f"e ={key.e}")
    print(f"d ={key.d}")
    print(f"p ={key.p}")
    print(f"q ={key.q}")

OK有了上面的代码基础之后，就可以解题了

常规解题

#出题脚本
from Crypto.PublicKey import RSA
import libnum
import gmpy2
import uuid

flag = "flag{" + str(uuid.uuid4()) + "}"
print(flag)
m = libnum.s2n(flag)

p = libnum.generate_prime(1024)
q = gmpy2.next_prime(p)
n = p * q
e = 65537
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = libnum.s2n(flag)
c = pow(m, e, n)
#
c1 = libnum.n2s(int(c))

with open("flag.pem", "wb") as f:
    f.write(c1)
# 生成公钥
rsa_components = (int(n), int(e), int(d))
keypair = RSA.construct(rsa_components)
with open('pubckey.pem', 'wb') as f:
    f.write(keypair.exportKey())

#正常解题脚本
from Crypto.PublicKey import RSA
import libnum
with open("flag.pem", 'rb') as f: #打开flag.pem文件，并读取内容
    c = int(f.read().hex(),16)    #将flag.pem文件内容转换为十六进制数，并转换为十进制数

with open("pubckey.pem", 'rb') as f: #打开pubckey.pem文件，并读取内容
    key = f.read()                   #读取pubckey.pem文件内容

rsakey = RSA.importKey(key)         #导入公钥
print(rsakey)                       #打印公钥信息

d = rsakey.d                         #获取私钥d
n = rsakey.n                         #获取n
m = pow(c,d,n)                       #计算m
print(libnum.n2s(m).decode())

公钥分解

#出题脚本
from Crypto.PublicKey import RSA
import libnum
import gmpy2
import uuid

flag = "flag{" + str(uuid.uuid4()) + "}"
print(flag)
m = libnum.s2n(flag)

p = libnum.generate_prime(1024)
q = gmpy2.next_prime(p)
n = p * q
e = 65537
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = libnum.s2n(flag)
c = pow(m, e, n)
#
c1 = libnum.n2s(int(c))

with open("flag1.pem", "wb") as f:
    f.write(c1)
# 生成公钥
rsa_components = (int(n), int(e))
keypair = RSA.construct(rsa_components)
with open('pubckey1.pem', 'wb') as f:
    f.write(keypair.exportKey())

#解题脚本
"""
解题思路
从题目可以看出p和q相近所以
可以直接拿n来开方
然后求出p就可以通过next_prime函数求出下一个素数
然后p和q都有了就可以求出phi_n和d
最后求出m就可以得到明文

"""


from Crypto.PublicKey import RSA
import libnum
import gmpy2
import sympy

with open("flag1.pem", 'rb') as f:
    c = f.read()                           # 读取密文
c=libnum.s2n(c)                            # 字符串转十进制
with open("pubckey1.pem", 'rb') as f:
    key = f.read()                         # 读取公钥
rsakey = RSA.importKey(key)                # 导入公钥
n= rsakey.n                                # 导入n
e= rsakey.e                                # 导入e
p1=libnum.nroot(n,2)                     #开平方根
p=gmpy2.next_prime(p1)                     #下一个素数
q=sympy.prevprime(p)                       #上一个素数
print(n==p*q)                              #判断是否为合数
phi=(p-1)*(q-1)                            #求欧拉函数
d=libnum.invmod(e,phi)                     #求私钥d
m=pow(c,d,n)                               #求明文m
print(libnum.n2s(int(m)).decode())         #输出明文

公钥OAEP

介绍

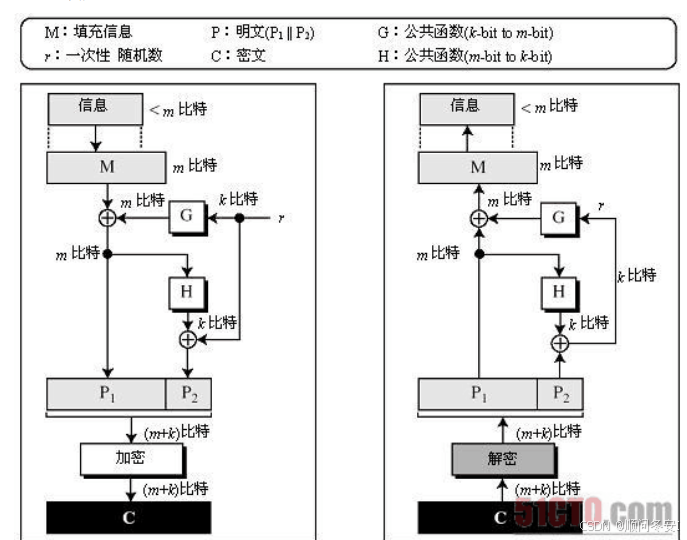
OAEP填充
把明文填充到1024bite，记为M。
选取一个随机数r（1024bite）。
把r进行G函数，此处的G函数为6次sha1，记为R。
把R和M进行异或得到P1。
把P1进行H函数，此处的H函数也为6次sha1，并和r进行异或处理得到P2。
把P1和P2进行合并得到OAEP填充完的字符串记为C。

#出题脚本
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
import libnum
import gmpy2
import uuid

flag = "flag{" + str(uuid.uuid4()) + "}"
print(flag)
flag = flag.encode()

p = libnum.generate_prime(1024)
q = gmpy2.next_prime(p)
n = p * q
e = 65537
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)

#
# 生成公钥
rsa_components = (int(n), int(e), int(d))
keypair = RSA.construct(rsa_components)
with open('prikey2.pem', 'wb') as f:
    f.write(keypair.exportKey())

rsa_components = (int(n), e,)
arsa = RSA.construct(rsa_components)
rsakey = RSA.importKey(arsa.exportKey())
rsakey = PKCS1_OAEP.new(rsakey)
c = rsakey.encrypt(flag)
with open("flag2.pem", "wb") as f:
    f.write(c)

#解题脚本
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
with open("flag2.pem", 'rb') as f:
    ciphertext = f.read()
with open("prikey2.pem", 'rb') as f:
    key = f.read()

rsakey = RSA.importKey(key)
cipher = PKCS1_OAEP.new(rsakey)
m = cipher.decrypt(ciphertext)
print(m.decode())