skyline查询——三种数据模型

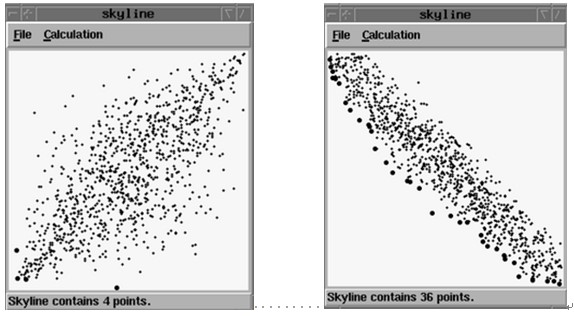
在2001年Stephan Borzsonyi提出天际线查询（Skyline Query）这个概念时，作者提出了三种分布类型的用于skyline查询实验的数据集生成方法。同时给出了生成这些类型测试数据集的源代码，这也成为后来“skyline计算”研究人员最常用的人工合成测试数据集的方法。
这三类型的测试数据集分别是独立数据集（independently），正相关数据集（correlated）和负相关（anti-correlated）数据集
![论文散点图](https://imgconvert.csdnimg.cn/aHR0cDovL2ltZy5ibG9nLmNzZG4ubmV0LzIwMTcxMjA5MDIyOTAyMDY5?x-oss-process=image/format,png)

而且在作者网站上提供了生成这三种数据集的源代码：

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#include <string>
#include <math.h>

#define MAXINT 2147483647
#define sqr(a) ((a)*(a))

using namespace std;

int Statistics_Count;
double* Statistics_SumX;
double* Statistics_SumXsquared;
double* Statistics_SumProduct;


void InitStatistics(int Dimensions)
// ==============
// initialisiert Z?hlvariablen der Statistik
{
    Statistics_SumX = new double[Dimensions];
    Statistics_SumXsquared = new double[Dimensions];
    Statistics_SumProduct = new double[Dimensions*Dimensions];
    
    Statistics_Count = 0;
    for (int d=0; d<Dimensions; d++) {
        Statistics_SumX[d]=0.0;
        Statistics_SumXsquared[d]=0.0;
        for (int dd=0; dd<Dimensions; dd++) Statistics_SumProduct[d*Dimensions+dd] = 0.0;
    }
}


void EnterStatistics(int Dimensions,double* x)
// ===============
// registiriert den Vektor "x" für die Statistik
{
    Statistics_Count++;
    for (int d=0; d<Dimensions; d++) {
        Statistics_SumX[d] += x[d];
        Statistics_SumXsquared[d] += x[d]*x[d];
        for (int dd=0; dd<Dimensions; dd++) Statistics_SumProduct[d*Dimensions+dd] += x[d]*x[dd];
    }
}


void OutputStatistics(int Dimensions)
// ================
// gibt die Statistik aus
{
    for (int d=0; d<Dimensions; d++) {
        double E = Statistics_SumX[d] / Statistics_Count;
        double V = Statistics_SumXsquared[d]/Statistics_Count - E*E;
        double s = sqrt(V);
        printf("E[X%d]=%5.2f Var[X%d]=%5.2f s[X%d]=%5.2f\n",d+1,E,d+1,V,d+1,s);
    }
    printf("\nKorrelationsmatrix:\n");
    for (int d=0; d<Dimensions; d++) {
        for (int dd=0; dd<Dimensions; dd++) {
            double Kov = (Statistics_SumProduct[d*Dimensions+dd]/Statistics_Count) -
            (Statistics_SumX[d]/Statistics_Count) * (Statistics_SumX[dd]/Statistics_Count);
            double Cor = Kov /
            sqrt(Statistics_SumXsquared[d]/Statistics_Count - sqr(Statistics_SumX[d] / Statistics_Count)) /
            sqrt(Statistics_SumXsquared[dd]/Statistics_Count - sqr(Statistics_SumX[dd] / Statistics_Count));
            printf(" %5.2f",Cor);
        }
        printf("\n");
    }
    printf("\n");
}


double RandomEqual(double min,double max)
// ===========
// liefert eine im Intervall [min,max[ gleichverteilte Zufallszahl
{
    double x = (double)rand()/MAXINT;
    return x*(max-min)+min;
}


double RandomPeak(double min,double max,int dim)
// ==========
// liefert eine Zufallsvariable im Intervall [min,max[
// als Summe von "dim" gleichverteilten Zufallszahlen
{
    double sum = 0.0;
    for (int d=0; d<dim; d++) sum += RandomEqual(0,1);
    sum /= dim;
    return sum*(max-min)+min;
}


double RandomNormal(double med,double var)
// ============
// liefert eine normalverteilte Zufallsvariable mit Erwartungswert med
// im Intervall ]med-var,med+var[
{
    return RandomPeak(med-var,med+var,12);
}


void GenerateDataEqually(FILE* f,int Count,int Dimensions)
// ===================
// generiert in der Datei "f" "Count" gleichverteilte Datens?tze
{
    InitStatistics(Dimensions);
    for (int i=0; i<Count; i++)
    {
        double x[Dimensions];
        for (int d=0; d<Dimensions; d++)
        {
            x[d] = RandomEqual(0,1);
            fprintf(f,"%8.6f ",x[d]);
        }
        EnterStatistics(Dimensions,x);
        fprintf(f,"\n");
    }
    OutputStatistics(Dimensions);
}


void GenerateDataCorrelated(FILE* f,int Count,int Dimensions)
// ======================
// generiert in der Datei "f" "Count" korrelierte Datens?tze
{
    InitStatistics(Dimensions);
    double x[Dimensions];
    for (int i=0; i<Count; i++) {
    again:
        double v = RandomPeak(0,1,Dimensions);
        for (int d=0; d<Dimensions; d++) x[d] = v;
        double l = v<=0.5 ? v:1.0-v;
        for (int d=0; d<Dimensions; d++) {
            double h = RandomNormal(0,l);
            x[d] += h;
            x[(d+1)%Dimensions] -= h;
        }
        for (int d=0; d<Dimensions; d++) if (x[d]<0 || x[d]>=1) goto again;
        for (int d=0; d<Dimensions; d++) fprintf(f,"%8.6f ",x[d]);
        EnterStatistics(Dimensions,x);
        fprintf(f,"\n");
    }
    OutputStatistics(Dimensions);
}


void GenerateDataAnticorrelated(FILE* f,int Count,int Dimensions)
// ==========================
// generiert in der Datei "f" "Count" antikorrelierte Datens?tze
{
    InitStatistics(Dimensions);
    double x[Dimensions];
    for (int i=0; i<Count; i++) {
    again:
        double v = RandomNormal(0.5,0.25);
        for (int d=0; d<Dimensions; d++) x[d] = v;
        double l = v<=0.5 ? v:1.0-v;
        for (int d=0; d<Dimensions; d++) {
            double h = RandomEqual(-l,l);
            x[d] += h;
            x[(d+1)%Dimensions] -= h;
        }
        for (int d=0; d<Dimensions; d++) if (x[d]<0 || x[d]>=1) goto again;
        for (int d=0; d<Dimensions; d++) fprintf(f,"%8.6f ",x[d]);
        EnterStatistics(Dimensions,x);
        fprintf(f,"\n");
    }
    OutputStatistics(Dimensions);
}


void GenerateData(int Dimensions,char Distribution,int Count, string FileName)
// ============
// generierte eine Datei mit zuf?lligen Daten
{
    if (Count <= 0) {
        printf("Ungültige Anzahl von Punkten.\n");
        return;
    }
    if (Dimensions < 2) {
        printf("Ungültige Anzahl von Dimensionen.\n");
        return;
    }
    switch (Distribution) {
        case 'E':
        case 'e': Distribution = 'E'; break;
        case 'C':
        case 'c': Distribution = 'C'; break;
        case 'A':
        case 'a': Distribution = 'A'; break;
        default: printf("Ungültige Verteilung.\n"); return;
    }
    
    FILE* f = fopen(FileName.data(),"wt");
    if (f == NULL) {
        printf("Kann Datei \"%s\" nicht anlegen.\n",FileName.data());
        return;
    }
    fprintf(f,"%d %d\n",Count,Dimensions);
    switch (Distribution) {
        case 'E': GenerateDataEqually(f,Count,Dimensions); break;
        case 'C': GenerateDataCorrelated(f,Count,Dimensions); break;
        case 'A': GenerateDataAnticorrelated(f,Count,Dimensions); break;
    }
    fclose(f);
    printf("%d Punkte generiert, Datei \"%s\".\n",Count,FileName.data());
}
主函数
int main(int argc, char** argv)
{
    //Verteilung = E(qually) | C(orrelated) | A(nti-correlated);
    
    GenerateData(2,'A',500, "data_anti_corr");
    GenerateData(2,'C',500, "data_correlate");

    return 0;
}

以下是笔者在Xcode on OSX10.11中运行的运行结果：

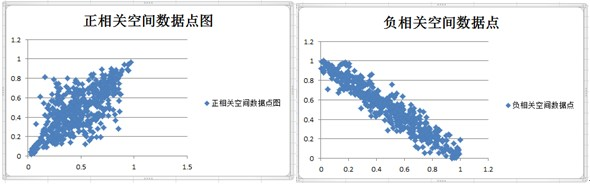
把这两个文件的数据通过Excel仿真出来结果如下：