Constructing Roads In JGShining's Kingdom
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 16037 Accepted Submission(s): 4576
Problem Description
JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.
Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.
With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.
Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.
The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.
But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.
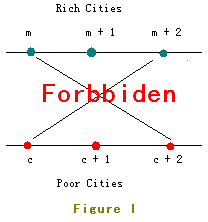
For example, the roads in Figure I are forbidden.
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^
Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.
With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.
Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.
The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.
But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.
For example, the roads in Figure I are forbidden.

In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^
Input
Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.
Output
For each test case, output the result in the form of sample.
You should tell JGShining what's the maximal number of road(s) can be built.
You should tell JGShining what's the maximal number of road(s) can be built.
Sample Input
2 1 2 2 1 3 1 2 2 3 3 1
Sample Output
Case 1: My king, at most 1 road can be built. Case 2: My king, at most 2 roads can be built.HintHuge input, scanf is recommended.
Author
JGShining(极光炫影)
解题思路:给你一些点分别分布在河的两岸,它们之间有一些线路,求使得线路之间两两不相交的最多有多少条线路,把河岸左边的点的序号从小到大排列,那么要求不相交的话,右边的点也必须从小到大排列,也就是说求右边点的最长上升子序列,但是这里n很大,所以用nlogn的方法来求
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define Max 500005
using namespace std;
struct Road
{
int a,b;
friend bool operator <(Road a,Road b)
{
return a.a<b.a;
}
}road[Max];
int a[Max],c[Max];
int find(int *a,int len,int n)//修改后的二分查找,若返回值为x,则a[x]>=n
{
int left=0,right=len,mid=(left+right)/2;
while(left<=right)
{
if(n>a[mid]) left=mid+1;
else if(n<a[mid]) right=mid-1;
else return mid;
mid=(left+right)/2;
}
return left;
}
int main()
{
int n,i,j,len,ncase=1;
while(~scanf("%d",&n))
{
memset(a,0,sizeof(a));
memset(c,0,sizeof(c));
for(i=1;i<=n;i++)
scanf("%d%d",&road[i].a,&road[i].b);
sort(road+1,road+1+n);
for(i=1;i<=n;i++)
a[i]=road[i].b;
c[0]=-1;c[1]=a[1];
len=1;
for(i=2;i<=n;i++)
{
j=find(c,len,a[i]);
c[j]=a[i];
len=max(len,j);
}
if(len==1)
printf("Case %d:\nMy king, at most %d road can be built.\n\n",ncase++,len);
else
printf("Case %d:\nMy king, at most %d roads can be built.\n\n",ncase++,len);
}
return 0;
}























 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








