Computer
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 4426 Accepted Submission(s): 2229
Problem Description
A school bought the first computer some time ago(so this computer's id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about
slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information.
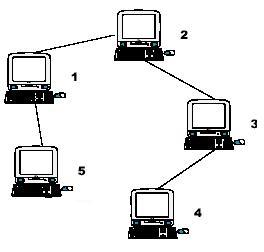
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.
Input
Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which
i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.
Output
For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).
Sample Input
5 1 1 2 1 3 1 1 1
Sample Output
3 2 3 4 4
现有结论,从任意一点u出发搜到的最远的点一定是s、t中的一点,然后在从这个最远点开始搜,就可以搜到另一个最长路的端点,即用两遍广搜就可以找出树的最长路
反之:若知道树直径的两个端点为S和T,每个点的最长路 要么是到S的距离 要么是到T的距离
所以我们可以先找到s -- t中的 s 点和 t 点,从 s 点 bfs一遍 可以得到 s 到各点的距离 d1 [ i ], 从 t 点 bfs 一遍可以得到 t 到各点的距离 d2[ i ],d1[ i ]和d2[ i ]较大的就每个点的最长路。
#include <cstdio>
#include <cstring>
#include <cstring>
#include <algorithm>
#include <queue>
#define maxn 11000
#define maxm 110000
using namespace std;
int dist[maxn], vis[maxn];
int head[maxn], cnt;
int dist1[maxn];
int S, T;
int n;
struct node{
int u, v, w, next;
};
node edge[maxm];
void init(){
cnt = 0;
memset(head, -1, sizeof(head));
}
void add(int u, int v, int w){
edge[cnt] = {u, v, w, head[u]};
head[u] = cnt++;
edge[cnt] = {v, u, w, head[v]};
head[v] = cnt++;
}
void getmap(){
for(int i = 2; i <= n; ++i){
int b, c;
scanf("%d%d", &b, &c);
add(i, b, c);
}
}
int bfs(int x){
queue<int>q;
memset(vis, 0, sizeof(vis));
memset(dist, 0, sizeof(dist));
vis[x] = 1;
q.push(x);
int ans = 0;
int nod = x;
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = head[u]; i != -1; i = edge[i].next){
int v = edge[i].v;
if(!vis[v]){
dist[v] = dist[u] + edge[i].w;
if(ans < dist[v]){
ans = dist[v];
nod = v;
}
vis[v] = 1;
q.push(v);
}
}
}
return nod;
}
int main (){
while(scanf("%d", &n) != EOF){
init();
getmap();
S = bfs(1);
T = bfs(S);
for(int i = 1; i <= n; ++i)
dist1[i] = dist[i];
bfs(T);
for(int i = 1; i <= n; ++i){
dist[i] = max(dist1[i], dist[i]);
printf("%d\n", dist[i]);
}
}
return 0;
}









 本文介绍了一种通过两次广度优先搜索(BFS)来确定树形网络中任意节点到最远节点距离的方法,该方法首先找到树的直径,进而求得每个节点的最长路径。
本文介绍了一种通过两次广度优先搜索(BFS)来确定树形网络中任意节点到最远节点距离的方法,该方法首先找到树的直径,进而求得每个节点的最长路径。
















 1983
1983

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








